YOLOv5用JAX从零复现

前置知识：YOLOv1笔记, YOLOv2,v3笔记, YOLOv4笔记

回顾YOLOv1到v4

YOLOv1

我们学会了YOLO的基础框架（一阶段端到端模型），将 $H\times W$ 的图像按照步长 $s$ (stride单位为像素) 划分为 $(H/s)\times (W/s)=: S\times S$ 的网格（这里默认图像输入的长宽相同，所以可以将网格大小记为 $S\times S$），每个网格内包含 $B=2$ 个预测框，每个识别框负责预测中心点在当前网格内的边界框。

预测框至少由6个参数确定：$(x,y,w,h,conf,cls)$，其中

• $(x,y)$ 表示当前边界框的中心点基于当前步长 $s$ 为缩放比例，原点为中心点所处网格左上角的相对坐标（不难发现 $x,y\in[0,1]$）；
• $(w,h)$ 表示当前边界框的长宽相对于当前步长 $s$ 为缩放比例；
• $conf$ 表示 $\text{Pr}(Object)\cdot \text{IOU}_{pred}^{true}$，也就是当前预测框和真实框的交并比（IOU）；
• $cls$ 表示当前预测框所属的类别（class）。

损失函数上全部使用MSE，只有对 $(w,h)$ 进行了开更号运算处理，损失函数如下：

$$\begin{aligned} &\ \lambda_{coord}\sum_{i=0}^{S^2}\sum_{j=0}^{B}\mathbb{1}_{ij}^{obj}\left[ \substack{ \displaystyle (x_i-\hat{x}_j)^2+(y_i-\hat{y}_j)^2\\ \displaystyle +\left(\sqrt{w_i}-\text{sign}(\hat{w}_j)\sqrt{|\hat{w}_j|}\right)^2+\left(\sqrt{h_i}-\text{sign}(\hat{h}_j)\sqrt{|\hat{h}_j|}\right)^2 } \right]\\ + &\ \sum_{i=0}^{S^2}\sum_{j=0}^B\mathbb{1}_{ij}^{obj}(1-\hat{c}_j)^2 + \lambda_{noobj}\sum_{i=0}^{S^2}\sum_{j=0}^B\mathbb{1}_{i}^{noobj}(0-\hat{c}_j)^2\\ + &\ \sum_{i=0}^{S^2}\mathbb{1}_{i}^{obj}\sum_{c=0}^{C}\bigg(p_i(c)-\hat{p}_i(c)\bigg)^2 \end{aligned}$$

其中 $\mathbb{1}_{ij}^{obj}\in\{0,1\}$，当且仅当，网格 $i$ 中存在一个真实框，且预测框 $j$ 是两个预测框中和真实框具有更大IOU的一个时，$\mathbb{1}_{ij}^{obj}=1$，否则为 $0$；$\mathbb{1}_{i}^{noobj}\in{0,1}$，当且仅当，网格 $i$ 中没有任何真实框时，$\mathbb{1}_{i}^{noobj}=1$，否则为 $0$。（简单来说上述两个boolean变量分别表示当前网格中是否包含真实框）

YOLOv1模型框架使用的是基于VGG模型魔改的DarkNet-24，激活函数为LeakyReLU。

YOLOv2, YOLOv3

YOLOv3相对YOLOv1有非常多改进，基本奠定了后续YOLO系列模型的基础框架。

1. 模型改进，在Backbone后引入Neck结构，即用Gauss金字塔思路（FPN）对图像特征进一步提取，不再是YOLOv1中的单头输出，而是采用多头输出，每个输出头输出不同网格步长的预测结果，每个输出头中的每个网格预测边界框数目为 $B=3$；网格步长通常取为 $8,16,32$，也就是用二维卷积分别下采样3,4,5次，所以在模型中常称之为 $P3,P4,P5$。

2. 在YOLO中引入 锚框（Anchor bounding box） 的概念，对每个预测框的长宽 $(w,h)$ 预测，从原来的直接预测，改变为预测相对于某个先验检测框（锚框）的长宽的比例系数 $(w_a,h_a)$ ，这样可以更快收敛（引入先验信息）。
   假设锚框的长宽为 $(A_w,A_h)$，则当前预测框的长宽为 $(A_ww_a,A_hh_a)$，锚框长宽的确定是通过对整个数据集中的所有边界框的长宽做K近邻（KNN） 求得；根据锚框面积的从小到大，对应网格的步长从小到大，分别对应分配锚框（模型包含三个输出头，每个输出头中的每个网格需要预测三种边界框，所以我们总共需要 $3\times 3=9$ 个不同大小的锚框）。

3. 损失函数使用BCE（二元交叉熵）作为 $(x, y), conf$ 项损失，softmax（多元交叉熵）作为 $cls$ 项损失。

4. 模型架构使用DarkNet-53，基于ResNet模型设计，使用LeckyReLU激活函数。

YOLOv3的损失函数和v4类似，这里不再阐述。

YOLOv4

YOLOv4有更多细节上的改进：

1. 模型Backbone结构：加入CSPNet结构（通过折半通道数，仅对其中一半进行操作，最后再合并通道，从而减小模型参数同时稳定性能的），使用Mish激活函数。

2. 模型Neck结构：将FPN改为PANet（一个Gauss金字塔变两个Gauss金字塔，两个金字塔之间的特征还要相互连接下）；加入SPP结构（用三个不同的max_pool步长5,9,13，对特征进行提取，最后再合并通道）

3. 检测头Head结构：与边界框相关的损失函数改为CIOU损失，$(w,h)$ 作用 $\big(2\sigma(\cdot)\big)^2$ 变换，从而将锚框的相对比例范围限制在 $(0,4)$ 之间（其中 $\sigma(\cdot)$ 表示Sigmoid函数），构造损失函数时候，只对锚框和真实框的长宽比例小于 $4$ 计算损失，这样也可以加快收敛；使用BCE作为 $cls$ 项的损失函数（此处只是为了取消在增强一个类别识别时候对其余类别识别的抑制作用）。

4. 数据增强：使用Mosaic增强方法（先在一个大图像上随机选一个中心点，然后从数据集中随机选四个图像，四个角各放一个，然后做随机平移旋转和hsv变换，最后裁剪回模型输入的图像大小，需要注意边界框也要随之变化）

YOLOv4的损失函数可以记为

$$\begin{aligned} \mathcal{L}(\hat{y}, y; \theta) = \sum_{i=1}^W\sum_{j=1}^H\sum_{k}^3&\ \mathcal{1}^{noobj}_{ijk}\lambda_{noobj}\text{BCE}(\hat{c}_{ijk},0)\\ &\ +\mathcal{1}^{obj}_{ijk}\bigg[\lambda_{box}\text{CIOU}(\widehat{box}_{ijk},box_{ijk}) + \lambda_{obj}\text{BCE}(\hat{c}_{ijk},\text{IOU}_{pred}^{true})\\ &\ \qquad\qquad+\lambda_{class}\text{BCE}\bigg(\{\hat{p}_{c_{ijk}}\}, \text{onehot}(class_{ijk}^{true})\bigg)\bigg] \end{aligned}$$

其中 $\hat{y} = (\widehat{box},\hat{c},\{\hat{p}\})$，分别为预测框的 $((x,y,w,h),conf,cls)$。

后续YOLO系列基本都采用该损失函数，并且 $\lambda_{noobj}$ 和 $\lambda_{obj}$ 通常采用相同的值。YOLOv5中基于输入图像大小为 $640\times 640$ 分类类别为 $80$ 个的情况，这里超参数为 $\lambda_{box}=0.05, \lambda_{obj}=\lambda_{noobj}=1.0, \lambda_{class}=0.5$，当图像大小变换后 $\lambda_{obj}$ 需要等比例变化，类别大小变化后 $\lambda_{class}$ 需要等比例变换。

YOLOv5

介绍完了上述YOLO系列的算法，我们再来看YOLOv5所作的改进：

1. 模型优化：模型框架和v4类似，使用简化后的CSPNet，删掉许多过度用的1x1卷积，同时保持性能（v5: 46,623,741 (186.5 MB)，v4: 64,407,901 (257.6 MB)）；

2. SPP速度优化：SPP就是用三种不同步长的max_pool，巧妙之处在于这三个步长5,9,13两两之间正好差5，所以可以用步长为5的max_pool重复做3次，就可以得到相同的三个结果，更小的步长计算速度还能更快。

大量的工程Tricks：

1. 由于减小了模型大小，所以可以将图像输入从 $442\times 442$ 增大到 $640\times 640$，图像越大模型更容易学到细节。

2. 每个真实框的中心点不再属于一个网格，而是相邻的两个网格都可以对该真实框进行识别，可以增多目标框的数目。

3. 累计梯度，设立一个名义上的Batchsize（Nominal batchsize）例如 $64$，假设当前喂给模型的数据batchsize为 $32$，则我们需要对计算出的梯度进行两次累加，再对参数进行一次更新。（注意这样需要对每次计算的总损失加上一个 $\dfrac{batchsize}{batchsize_{nominal}}$ 的系数）

4. 检测头偏置初始化，参考Focus Loss论文中3.3章节给出的初始化思路，实际在4.1章节的Initialization部分，通过 $\log(\pi/(1-\pi))$ 对检测头的偏置进行初始化，这里的 $\pi$ 就是平均整个数据集中对于当前预测目标的真实值占比（由于 $\pi$ 一般很小，所以近似用 $\log(\pi)$ 代替）。比如类别预测中，类别 $c_1$ 对应的 $\pi$ 就应该是类别 $c_1$ 的边界框数目在整个数据集中的占比；$conf$预测中，对应的 $\pi$ 就是每个输出头所预测的真实框数目占整个输出头的全部预测框比例。

bias = bias.at[:, 4].set(jnp.log(8 / (args.image_shape[0] / s) * (args.image_shape[1] / s)))  # assume 8 target boxes per image
bias = bias.at[:, 5:].set(jnp.log(0.6 / (args.num_classes - 1 + 1e-6)))  # the distribution for each class in dataset

5. 学习率schedule：在warmup阶段（前3个epochs），模型中所有可学习的Bias项（包括BatchNormal里面的）的学习率从 $0.1$ 到 $0.01$，其余可学习参数的学习率从 $0$ 到 $0.01$，后续学习率变化均采用从 $0.01$ 到 $0.0001$ 的线性变换（可以尝试cosine学习率变换）。

6. 对验证模型的参数更新使用指数移动平均EMA(Exponential Moving Average)，即一种随着训练进行，对验证模型的参数更新速度逐渐减缓的更新策略。假设当前训练的参数为 $\theta$，验证的模型参数为 $\tilde{\theta}$，根据每次 $\theta$ 参数更新时，对 $\tilde{\theta}$ 进行如下更新：

$$\tilde{\theta}\gets d_t\tilde{\theta} + (1 - d_t) \theta$$

其中 $d_t = d_0\cdot (1 - \exp(-t / \tau))$，$t=1,2,\cdots$ 表示模型的更新次数，$d_0=0.9999,\tau=2000$。我们知道当 $d_t = 1 - 1/t$ 时候表示求平均，指数平均可以理解为对求平均加上了一个指数分布，对于 $t$ 比较小的参数更新幅度较大，后面更新幅度越来越小。

模型架构示意图参考YOLOv5官方 Ultralytics YOLOv5 Architecture 给出的：

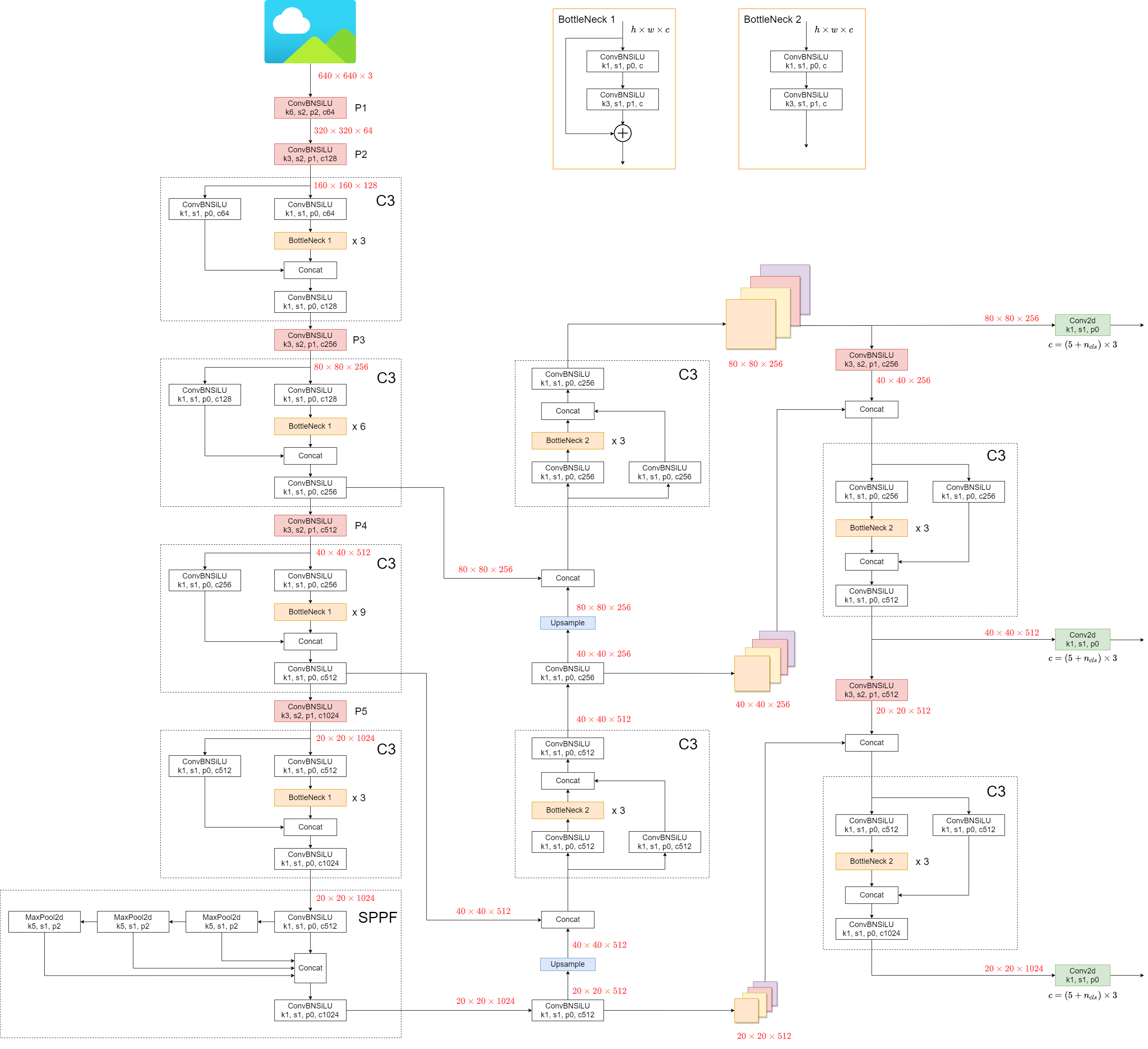
JAX代码复现

在COCO数据集上实现YOLOv5的复现，核心代码：KataCV/yolov5，分为以下这16个文件：

- katacv/
  - yolov5/
    - cfg.py  # 模型参数配置文件config
    - logs.py  # 模型callback，打印所需的参数到tensorboar和wandb中
    - loss.py  # 对YOLOv5模型损失函数进行计算，基于输入数据构建target，并对模型参数进行更新
    - model.py  # 搭建YOLOv5模型的Neck和Head部分
    - new_csp_darknet53.py  # 搭建YOLOv5的Backbone部分
    - parser.py  # 使用argparse对超参数指令进行解析
    - predict.py  # 对YOLOv5模型做推断预测，并记录预测结果，用于计算AP@50,AP@75,mAP等指标
    - process_mp4.py  # 使用训练好的YOLOv5模型对mp4文件进行识别
    - train.py  # 对YOLOv5模型进行训练
    - train_state.py  # 定义YOLOv5模型训练状态类TrainState
    - val.ipynb  # 对YOLOv5模型进行验证调试
  - utils/
    - yolo/
      - build_dataset.py  # 对数据集进行读取，并做Mosaic，仿射变换和hsv数据增强
      - predictor.py  # 用于AP指标的计算
      - utils.py  # 和build_dataset相关的函数
    - detection/
      - __init__.py  # 可视化边界框，计算各种IOU，计算NMS
      - utils_ap.py  # 和predictor相关的用于AP指标计算的函数

训练结果

当前batchsize为32，图像大小为 $640\times 640$，训练 $50$ epoch 已达到 58.6% AP@50, 42.78% AP@75, 39.92% mAP@[50:95:5]，总计要训练 $300$ epochs（预计5.4天，RTX4090上一个epoch训练+验证需要26mins，在RTX4080上需要36mins），等待训练结果（2024.1.18）。训练到160epoch左右基本收敛，各项指标如下（YOLOv5(JAX)为187epoch下的结果）：

模型	P@50	R@50	AP50	AP75	mAP	Size	FPS
YOLOv5(JAX)	48.57%	70.2%	62.97%	48.11%	44.64%	640	80
YOLOv4(paper)	NAN	NAN	65.7%	47.3%	43.5%	608	62
YOLOv5(offical)$^*$	60.24%	72.38 %	66.02%	NAN	47.32%	640	100

YOLOv5(offical)$^*$ 为自己测试YOLOv5官方代码的结果：

python train.py --data coco.yaml --epochs 300 --weights '' --cfg yolov5l.yaml --batch-size 32

Check training result on WandB/在WandB上查看实时训练结果

实现细节

代码实现中的细节问题非常多，例如：

1. CIOU损失中必须对 $alpha$ 系数做梯度截断（还需做验证是否需要判断系数S，是否可以截断DIOU中对角线长度的梯度）。
2. YOLO Loss中计算完CIOU损失后，用于计算conf损失前，需要截断ciou的梯度。
3. CIOU中的边界框(x,y,w,h)，其中 $x,y$ 相对当前网格左上角缩放比例为步长 $s$，$w,h$ 是 $(A_ww_a/s,A_hh_a/s)$，其中 $(A_w,A_h)$ 为锚框大小，$(w_a,h_a)$ 为模型预测出的相对锚框的比例。
4. 对每个target中每一项求loss后，需要对非零项求平均值。
5. 检测模型的最后输出是预测出的维度为 $(B,S,S,255)$，其中 $B$ 表示batchsize，$S$ 表示网格的大小。由于每个网格给出3个预测框，我们期望将每个预测框预测结果重整一下，这里注意不要直接reshape为 $(B,3,S,S,85)$，这样会导致按照通道顺序进行拉伸，我们需要按照图像长宽进行拉伸，也就是先 reshape(B,S,S,3,85)，再 transpose(0,3,1,2,4) 才行，直接 reshape 的训练结果就是上面WandB中训练速度明显偏低的那些。（最离谱的是在复现YOLOv4时候也犯了这个错误，导致其训练效果极差，不然估计我都不会来复现YOLOv5了🤣）

以下是我的代码更新日志（在train.py的开头部分）：

2023/12/22: Start training on my RTX4080.
Fix bugs:
1. Calculating mean loss should use mask.sum() as denominator.
2. Forget stopping gradient when calculating object loss.
3. Fix the prediction function for confidence calculating.
4. Update self.state in predictor for evaluating metrics in-time [must pass new state].
2023/12/23: Use 30 batch size, 97% GPU memory
2023/12/25: Training 79 epochs found no weight decay and gradient norm clip (max_norm=10.0)!
2023/12/26: Update nms iou_thre=0.65, use IOU metrics (old: DIOU),
  add more buffer `max_num_box*30` to nms (old: `max_num_box*9`)
2023/12/27: Update CIOU: `wh` relative to cell.
2023/12/29: Found mAP, AP50, AP75 jump huge after 40 epochs.
  1. Add stopping gradient of DIOU diagonal distance.
  2. Add accumulate gradient to nominal batch size 64. (start train 16 batch size)
2023/12/30: FIX BUG:
  1. Fix weight decay coef size for accumulating gradient.
2024/1/1: FIX BUG:
  1. Loss calculate `train=train`. (Huge different result whether turn on the batch normalize)
  2. Check paper https://arxiv.org/pdf/1906.07155.pdf section 5.2,\
    when use pretrain backbone model, we must freeze BN statistic in backbone model,\
    also we can use 2x learning rate.
2024/1/9: Complete training from scratch (on RTX 4090): batch=32, nominal batch=64, val result:
p: 0.488 r: 0.612 ap50: 0.559 ap75: 0.402 map: 0.379: 100%|██████████| 156/156 [01:28<00:00,  1.76it/s]
2024/1/15: Fix BUG:
1. backbone stage size = [3,6,9,3] and CSP bottleneck channel is output_channel // 2
  YOLOv5: Total Parameters: 46,623,741 (186.5 MB)
Add:
1. Two different learning rate schedule for 'bias' and other weights.
2. Add focus loss initialization, -log(pi) in `model.py`.
Modify:
1. Change decayed weights to optax, should be faster.
2024/1/16: FIX BUG:
1. Detection model output predict, `ScalePredictor` should not reshape logits directly
  that will make wrong dimension exapand. (First reshape then transpose!)
  This change makes training mush faster (x10 epoch).
Add:
1. Add EMA(Exponential Moving Average): `d0 * (1 - exp(-t / tau))`, `t` is the update times.