三角多项式:
Pn=2a0+k=1∑n{akcoskx+bksinkx}
称为三角多项式,若 an 或 bn=0,则 degree(Pn)=n,可以将 Pn 视为 (eix)k 的多项式。
定理(Weierstrass 定理)
设 f∈C(R) 为 2π 周期函数,则存在三角多项式 Pn, degree(Pn)⩽n, n=1,2,⋯,使得 Pn⇒f(一致收敛)。
思路: 证明 Pn 为 σn 时成立(σn 为上一个 note 中所定义的,是 f 的 Fourier 级数的 Cesaˋro 和),再对两者差值进行估计,方法和 Fejeˊr 定理 证明思路类似。
证明: 由于 f 为连续的周期函数,则 ∣f∣⩽M 且 f 一致连续,即 δ→0lim∣x1−x2∣⩽δsup∣f(x1)−f(x2)∣=0,取
Pn=σn=n1(f1+⋯+fn)
下证 σn⇒f,
σn−f=⩽=∫0π2f(x+t)−f(x)+f(x−t)−f(x)En(t)dt∫0δ2f(x+t)−f(x)+f(x−t)−f(x)dt+∫δπ4MEn(t)dt I1+I2取0<δ<π
分别对 I1,I2 进行估计
∣I1∣⩽2∣x1−x2∣⩽δsup∣f(x1)−f(x2)∣∣I2∣⩽4Mnδ2C
对 ∀ε>0,∃0<δ<π,使得 ∣I1∣⩽2ε,则要使得 4Mnδ2C⩽2ε,则 n⩾δ2ε8MC,于是令 N=[δ2ε8MC]+1,所以当 n⩾N 时,有
⇒⇒ ∣σn(x)−f(x)∣⩽ε σn⇒f(x) Pn⇒f(x)
QED
这就说明了任何一个连续函数可以通过三角多项式逼近。
之前所使用的 f∈L1([a,b]),f:[a,b]→R,等价于 f Riemann 可积 或 f 有有限个奇点且 ∫ab∣f∣ 收敛,记
∣∣f∣∣1=∫ab∣f∣
称为 f 的 1-范数,类比的给出2-范数的定义。
2-范数
定义1(2-范数)
设 f:[a,b]→R,若 f Riemann 可积 或 f 有有限个奇点且 ∫ab∣f∣2 收敛,则称 f 可积或平方可积,记为 f∈L2([a,b]),当 ∫abf2<+∞ 时,f 平方可积,记
∣∣f∣∣2=(∫abf2)21
称为 f 的 2-范数。
2-范数很特别,因为在 L2([−π,π]) 有一组基,所以它是一个线性空间,并且可以类比向量空间(欧式空间) Rn,类似的定义有内积,正交的概念。
命题2(L2包含于L1)
设 f∈L2([a,b]),则 f∈L1([a,b])。
证明: 当 f Riemann 可积 时,显然 f∈L1([a,b]),下讨论有奇点的情况:
∫ab∣f∣=⩽=∫ab∣f∣⋅1 21∫ab(∣f∣2+1) 21∫ab∣f∣2+21(b−a)<+∞
则 ∫ab∣f∣ 收敛,故 f∈L1([a,b])。
QED
命题3(L2中的函数可以用光滑函数逼近)
设 f∈L2([a,b]), ∀ε>0, ∃g∈C∞([a,b]) 使得
∣∣f−g∣∣2⩽ε
证明: 由命题2可知,f∈L2([a,b])⇒f∈L1([a,b]),又由于 L1 中的函数都可以由光滑函数逼近 (详见 note11 - 命题2(光滑函数逼近)),则存在光滑函数 g 使得
∣f−g∣⩽ε
则
∣∣f−g∣∣2=(∫ab(f−g)2)21⩽(∫abε2)21=b−a⋅ε
QED
命题4(线性性)
设 f,g∈L2([a,b]), α,β∈R,则 αf+βg∈L2([a,b])。
证明: 只讨论有奇点的情况
∫ab(αf+βg)2=⩽=∫ab{α2f2+β2g2+2αβ⋅f⋅g}∫ab{α2f2+β2g2+α2f2+β2g2} 2α2∫abf2+2β2∫abg2<+∞
QED
命题5(Cauchy - Schwarz)
设 f,g∈L2([a,b]),则 fg∈L1([a,b]),且
∣∣∣∣∣∣∫abfg∣∣∣∣∣∣⩽∣∣f∣∣2⋅∣∣g∣∣2
证明: 由 Cauchy−Scharz 不等式,知
(∫abfg)2⩽∫abf2⋅∫abg2∣∣∣∣∣∣∫abfg∣∣∣∣∣∣⩽(∫abf2)21⋅(∫abg2)21=∣∣f∣∣2⋅∣∣g∣∣2<+∞
QED
定义6(内积)
设 f,g∈L2([a,b]),定义
⟨f,g⟩=∫abfg
称 ⟨f,g⟩ 为 f,g 的内积。
命题7(内积的性质)
设 f,g,h∈L2([a,b]), α,β∈R,则
-
⟨f,g⟩=⟨g,f⟩(交换律)
-
⟨αf+βg,h⟩=α⟨f,h⟩+β⟨g,h⟩(分配律,积分的线性性)
-
∣⟨f,g⟩∣⩽∣∣f∣∣2⋅∣∣g∣∣2(命题5,内积小于边长乘积)
-
∣∣f∣∣2=⟨f,f⟩(函数的长度)
命题8(长度的性质)
设 f,g∈L2([a,b]), k∈R,则
-
∣∣f∣∣2⩾0
-
∣∣kf∣∣2=∣k∣⋅∣∣f∣∣2
-
(三角不等式)
∣∣∣∣∣∣∣f∣∣2−∣∣g∣∣2∣∣∣∣∣⩽∣∣f±g∣∣2⩽∣∣f∣∣2+∣∣g∣∣2
证明: 只证明第三条,由于
∣∣f±g∣∣22=⟨f±g,f±g⟩=∣∣f∣∣22+∣∣g∣∣22±2⟨f,g⟩
利用命题7第三条,得
∣∣f∣∣22−2∣∣f∣∣2⋅∣∣g∣∣2+∣∣g∣∣22⩽⇒ (∣∣f∣∣2−∣∣g∣∣2)2⩽⇒ ∣∣∣∣∣∣∣f∣∣2−∣∣g∣∣2∣∣∣∣∣⩽ ∣∣f±g∣∣2⩽∣∣f∣∣22+2∣∣f∣∣2⋅∣∣g∣∣2+∣∣g∣∣22 ∣∣f±g∣∣2⩽(∣∣f∣∣2+∣∣g∣∣2)2 ∣∣f±g∣∣2⩽∣∣f∣∣2+∣∣g∣∣2
QED
定义9(正交)
设 f,g∈L2([a,b]),若 ⟨f,g⟩=0,则称 f,g 正交,记为 f⊥g。
第二部分的目标是证明 L2([−π,π]) 是线性空间,且它的一组正交基为
{21,sinkx,coskx:k=1,2,⋯}
命题10(勾股定理)
设 f,g∈L2([a,b]),若 f⊥g,则
∣∣f+g∣∣22=∣∣f∣∣22+∣∣g∣∣22
利用 ∣∣f+g∣∣22=⟨f+g,f+g⟩,展开即可证明。
定义11(2-范数收敛)
设 fn,f∈L2([a,b]),n=1,2,⋯,若 ∣∣fn−f∣∣2→0 (n→+∞),则称 fn 依2-范数收敛到 f,记为
fn⟶L2f
不难发现函数项级数收敛性有如下关系:
fn⇒f (一致收敛)可推出 fn→f (逐点收敛)和 ⟶L2,由于
(∫ab(fn−f)2)21⩽b−a⋅[a,b]sup∣fn−f∣⩽b−a⋅ε
而逐点收敛和依 L2 收敛无法互推。
命题12(向量收敛则长度收敛)
设 f,fn∈L2([a,b]), n=1,2,⋯,若 fn⟶L2f(n→+∞),则
∣∣fn∣∣2→∣∣f∣∣2(n→+∞)
证明: 由命题8 三角不等式得
∣∣∣∣∣∣∣fn∣∣2−∣∣f∣∣2∣∣∣∣∣⩽∣∣fn−f∣∣2→0
QED
命题13(向量收敛则内积收敛)
设 fn,gn,f,g∈L2([a,b]), n=1,2,⋯,若 fn⟶L2f,gn⟶L2g,则
⟨fn,gn⟩⟶L2⟨f,g⟩
证明:
∣⟨f,g⟩−⟨fn,gn⟩∣==⩽ ∣⟨f,g⟩−⟨fn,g⟩+⟨fn,g⟩−⟨fn,gn⟩∣ ∣⟨f−fn,g⟩+⟨fn,g−gn⟩∣ ∣∣f−fn∣∣2⋅∣∣g∣∣2+∣∣fn∣∣2⋅∣∣g−gn∣∣2→0
QED
Fourier级数依L2收敛
若 f:R→R, f∣∣∣∣∣[−π,π]∈L1([−π,π]) 周期为 2π,且 Lipschitz 连续,则 fn→f 逐点收敛,即
f(x)=2a0+k=1∑∞{akcoskx+bksinkx}
类似是否有 f∣∣∣∣∣[−π,π]∈L2([−π,π]),是否有 fn⟶L2f,即 f 的 Fourier 级数依 L2 收敛于 f,
f(x)L22a0+k=1∑∞{akcoskx+bksinkx}
答案是肯定的,下面以定理的形式写出。
定理1(Fourier级数依L2收敛)
设 f∈L2([−π,π]),记
ak=π1∫−ππf(x)coskxdx(k=0,1,2,⋯)bk=π1∫−ππf(x)sinkxdx(k=1,2,⋯)fn=2a0+k=1∑n{akcoskx+bksinkx}
则 ∣∣fn−f∣∣2→0(n→+∞)。
由此看出
{21,coskx,sinkx:k∈Z⩾1}
为 L2([−π,π]) 上的一组正交基。
该命题证明较之前证明 fn 逐点收敛更为几何化,而不需要大量的运算,主要是利用函数的向量的性质
下面定义一些记号,设 f,g∈L2([−π,π]),fn 为 f 的 Fourier 级数的前 n+1 项和,则通过定义可得
(f−g)n=fn−gn
记
An=span{21,cosmx,sinkx:m,k=1,2,⋯,n}
其中 span 为基的扩张,则 fn∈An。
引理1(fn 为 f 在 An 空间上的投影)
-
(正交性)⟨f−fn,p⟩=0∀p∈An
-
(Bessel 不等式)∣∣fn∣∣2⩽∣∣f∣∣2
-
(最佳 L2 逼近)∣∣f−fn∣∣2⩽∣∣f−p∣∣2∀p∈An
思考:
由于 An 是由一组正交基扩张而成的,仔细观察 fn 的定义式,可以发现
ak=π1∫−ππf(x)coskxdx=π1⟨f(x),coskx⟩bk=π1∫−ππf(x)sinkxdx=π1⟨f(x),sinkx⟩
所以
fn== 2a0+k=1∑n{akcoskx+bksinkx} π2⟨f(x),21⟩⋅21+k=1∑n{π1⟨f(x),coskx⟩coskx+π1⟨f(x),sinkx⟩sinkx}
考虑在向量空间中,一个向量如何做一个面上的投影。
设 x∈Rn+1,则对于 Rn+1 中的一个平面的正交基
{e1,e2,⋯,en}
x 在这个面上的投影可以表示成如下形式
x=⟨e1,e1⟩⟨x,e1⟩e1+⟨e2,e2⟩⟨x,e2⟩e2+⋯+⟨en,en⟩⟨x,en⟩en=k=1∑n⟨ek,ek⟩⟨x,ek⟩ek
而 fn 的表达式,正好满足了该式,所以 fn 可以理解为 f 在 An 上的投影,下面给出严格证明。
证明:
⟨fn,21⟩=∫−ππ2a0⋅21=2π4a0=2π⋅π1∫−ππf=∫−ππf⋅21=⟨f,21⟩ ⟨fn,coskx⟩=∫−ππakcos2kx=πak=π⋅π1∫−ππf(x)⋅kxdx=∫−ππf(x)coskxdx=⟨f,coskx⟩ ⟨fn,sinkx⟩=∫−ππaksin2kx=πak=π⋅π1∫−ππf(x)⋅kxdx=∫−ππf(x)sinkxdx=⟨f,sinkx⟩
则对于 An 中的任意一个基 ek,都有 ⟨f−fn,ek⟩=0,由于 ∀p∈An,p=∑k=0nakek (ak∈R),则
⟨f−fn,p⟩=k=0∑nak⟨f−fn,ek⟩=0
- 由于 fn∈An,通过1.结论,⟨f−fn,fn⟩=0,由勾股定理,得
⇒⇒ ∣∣f∣∣22=∣∣f−fn∣∣22+∣∣fn∣∣2 ∣∣f∣∣22⩾∣∣fn∣∣22 ∣∣f∣∣2⩾∣∣fn∣∣2
⇒⇒∣∣f−p∣∣22=∣∣f−fn+fn−p∣∣22=∣∣f−fn∣∣22+∣∣fn−p∣∣22∣∣f−p∣∣22⩾∣∣f−fn∣∣22∣∣f−p∣∣2⩾∣∣f−fn∣∣2
引理2(连续函数的Fourier级数依二范数收敛)
设 f∈C([−π,π]), f(−π)=f(π),则 fn⟶L2f。
证明: 设 f~:R→R 为 2π 周期函数,且 f~∣∣∣∣∣[π,π]=f,则 f~∈C(R),由 Weierstrass 定理 知,存在 Pn∈An 使得 Pn⇒f~,则 Pn⟶L2f~,所以
⇒⇒ ⇒ ∫−ππ∣Pn−f~∣2→0∫−ππ∣Pn−f∣2→0∣∣Pn−f∣∣22→0∣∣Pn−f∣∣2→0
又由最佳 L2 逼近,得
⇒ ∣∣Pn−f∣∣2⩾∣∣fn−f∣∣2 ∣∣fn−f∣∣2→0
QED
引理3(L2中的函数可以由连续函数依L2逼近)
设 f∈L2([−π,π]),∀ε>0,则 ∃h∈C([−π,π]),且 h(−π)=h(π) 使得 ∣∣f−h∣∣2⩽ε。
证明: 由 命题3 - L2中的函数可以用光滑函数逼近 知,f 可由光滑函数逼近,则 ∃g∈C([−π,π]),使得 ∣∣g−f∣∣2⩽2ε,令 ∣g∣⩽M,
h(x)=⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧δg(−π+δ)(x+π),g(x),δg(π−δ)(x−π),[−π,−π+δ];(−π+δ,π−δ);[π−δ,π].
则
∣∣h−g∣∣22=∫−ππ(g−h)2⩽2∫−π−π+δ(2M)2=8δM2
为使得 8δM⩽2ε,则 δ⩽32M2ε2 时,∣∣h−g∣∣2⩽2ε。
综上,
∣∣f−h∣∣2⩽∣∣f−g∣∣2+∣∣g−h∣∣2⩽ε
QED
h(x) 函数的构造方法可以参考下图:
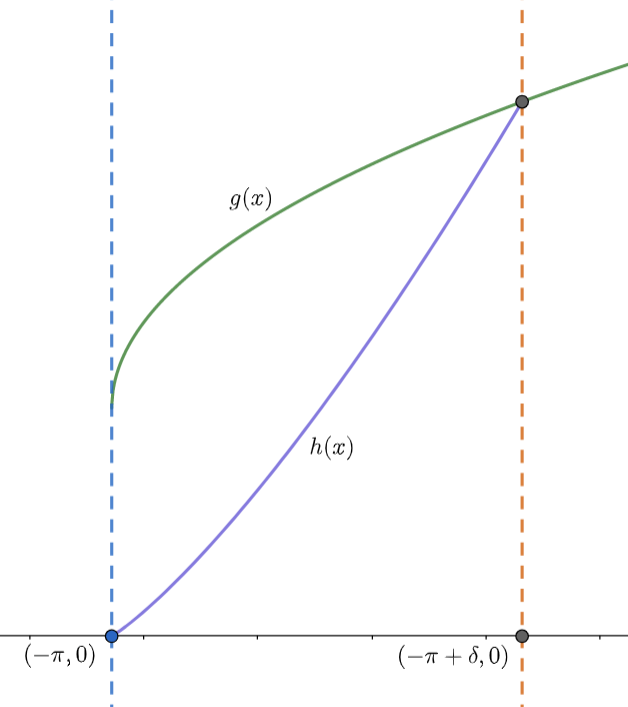 构造端点值相等的函数逼近方法
构造端点值相等的函数逼近方法
定理的证明
思路: 由引理2知,一个连续的周期函数 g(要求端点值相等),满足 gn⟶L2g,由引理3知,f∈L2,f 可由连续周期函数 g 逼近,通过估计即可证明定理。
证明: ∀ε>0,由引理3知,∃h∈C([−π,π]), h(−π)=h(π),使得 ∣∣f−h∣∣2⩽4ε,则
∣∣fn−f∣∣2⩽∣∣hn−h∣∣2+∣∣hn−fn∣∣2+∣∣f−h∣∣2
其中 ∣∣hn−fn∣∣2=∣∣(h−f)n∣∣2⩽∣∣h−f∣∣2(Bessel 不等式)。
所以
∣∣fn−f∣∣2⩽∣∣hn−h∣∣2+2ε
由引理2知,hn⟶L2h,则 ∃N∈Z>0,使得 ∀n⩾N,有 ∣∣hn−h∣∣2⩽2ε。
综上,
∣∣fn−f∣∣2⩽∣∣hn−h∣∣2+2ε⩽ε
QED
定理2(两个函数L2内积的表达式)
设 f,g∈L2([−π,π]),
f∼2a0+k=1∑∞{akcoskx+bksinkx}g∼2c0+k=1∑∞{ckcoskx+dksinkx}
则
π1∫−ππfg=π1∫−ππf2= 2a0c0+k=1∑∞{akck+bkdk} 2a02+k=1∑∞{ak2+bk2}Parseval 恒等式
证明: 由定理1知,fn⟶L2f, gn⟶L2g,由命题13和 An 是一组正交基,知
⟨f,g⟩=n→∞lim⟨fn,gn⟩=== n→∞lim{⟨2a0,2c0⟩+k=1∑n{⟨akcoskx,ckcoskx⟩+⟨bksinkx,dksinkx⟩}} n→∞lim{π2a0c0+k=1∑n{πakck+πbkdk}} π{2a0c0+k=1∑∞{akck+bkdk}}
令 g=f,第二个式子成立。
QED
定理3(对三角多项式积分)
设 f∈L2([−π,π]),且
f∼2a0+k=1∑∞{akcoskx+bksinkx}
令 [a,b]⊂[−π,π],则
∫abf=∫ab2a0dx+k=1∑∞{∫abakcoskx+∫abbksinkx}
证明: 由于
∫abfn=∫ab2a0dx+k=1∑n{∫abakcoskx+∫abbksinkx}
又由于
∣∣∣∣∣∣∫abfn−∫abf∣∣∣∣∣∣=⩽⩽⩽ ∣∣∣∣∣∣∫ab(fn−f)∣∣∣∣∣∣ ∫ab∣fn−f∣⋅1 (∫ab∣fn−f∣2)21(∫ab1)21 b−a⋅ε
则
⇒⇒∫abfn→∫abf(n→∞)∫abf=∫ab2a0dx+n→∞limk=1∑n{∫abakcoskx+∫abbksinkx}∫abf=∫ab2a0dx+k=1∑∞{∫abakcoskx+∫abbksinkx}
QED
定理4
设 f,g∈C([−π,π]),
f∼2a0+k=1∑∞{akcoskx+bksinkx}g∼2c0+k=1∑∞{ckcoskx+dksinkx}
(1). 如果 ak=0, k=0,1,2,⋯, bk=0, k=1,2,⋯,则 f≡0
(2). 如果 ak=ck, k=0,1,2,⋯, bk=dk, k=1,2,⋯,则 f≡g
证明:
(1). 由定理2知,
∫−ππf2=π{2a02+k=1∑∞{ak2+bk2}}=0
由 f 连续可知 f≡0。
(2). 由于 (f−g)n=fn−gn,即三角多项式系数相减,则 fn−gn 的系数均为 0,由(1)知,
f−g≡0⇒f≡g
QED
