字符串相关算法
字符串
Trie树
UVA - 1401 - Remember the Word - Trie+DP组合,UVA - 11732 - “strcmp()” Anyone? - Trie
#define reset(A) memset(A, 0, sizeof(A))
const int maxnode = ...;
const int maxc = ...;
struct Trie {
// 如果字符集较大可以考虑用map<char, int> ch[maxnode]代替
int ch[maxnode][maxc], val[maxn], sz; // 注意:这里数组全部为int
void init() { sz = 1; val[0] = 0; reset(ch[0]); } // 根节点默认为0,根据情况初始化val[0]
int id(char c) { return c - 'a'; } // 将字符转为索引
void insert(char *s, int v) {
int p = 0;
for (int i = 0; s[i]; i++) {
int c = id(s[i]);
if (!ch[i][c]) {
val[sz] = 0; reset(ch[sz]);
ch[i][c] = sz;
}
p = ch[i][c];
}
val[p] = v;
}
int query(char *s, ...) {...} // 思路与insert类似,都是顺序查找
}trie;KMP
KMP主要思路是计算模式串每个位置的失配位置fail[i],换句话说fail[i]表示字符串s[0,...,i-1]的最长前缀与后缀相同的长度(长度小于i),fail[i] = max{k:s[0,...,k-1] = s[i-k,...,i-1], k < i},生成方法运用DP+贪心的方法,通过第fail[i]求出fail[i+1]。
练习题:UVA - 1328 - Period - KMP求解字符串的最小周期长度,这道题给出了KMP的重要性质:
当
(i-fail[i])|i时(a|b表示a整除b),i-fail[i]为它的最小周期长度。
const int maxn = 1e6 + 10;
struct KMP {
int fail[maxn];
void getfail(char *P) {
fail[0] = fail[1] = 0;
for (int i = 1; P[i]; i++) {
int j = fail[i];
while (j && P[i] != P[j]) j = fail[j];
fail[i+1] = (P[i] == P[j]) ? j+1 : 0; // 第i位的计算得到的是i+1位的失配位置
}
}
void find(char *T, char *P) {
getfail(P);
for (int i = 0, j = 0; T[i]; i++) {
while (j && T[i] != P[j]) j = fail[j];
if (T[i] == P[j]) j++;
if (!P[j]) printf("%d\n", i-j+2);
}
}
}kmp;Aho-Corasick Automaton
AC自动机就是Trie树和KMP算法的结合,将KMP算法中的失配跳转,转化为失配边跳转。
// 在主程序中记得执行ac.init()进行初始化,否则程序输出全是0
struct AhoCorasickAutomaton {
int ch[maxnode][26], sz, val[maxnode]; // Trie part
void init() { sz = 1, val[0] = 0, reset(ch[0]); }
int id(char c) { return c - 'a'; }
void insert(char *s, int v) {
int p = 0;
for (int i = 0; s[i]; i++) {
int c = id(s[i]);
if (!ch[p][c]) {
val[sz] = 0, reset(ch[sz]);
ch[p][c] = sz++;
}
p = ch[p][c];
}
// 对于同一个串,如果有多个重复指标,选择第一个作为代表元representation
if (val[p]) repr[v] = val[p];
else val[p] = v, repr[v] = v;
}
int q[maxnode], tail, last[maxnode], fail[maxnode], cnt[maxnode]; // AC part
void getfail() {
tail = -1; fail[0] = 0;
for (int c = 0; c < 26; c++) {
int v = ch[0][c];
if (v) q[++tail] = v, last[v] = fail[v] = cnt[v] = 0;
}
for (int head = 0; head <= tail; head++) { // 用广度优先搜索完成fail数组创建,可以理解为拓朴排序
int u = q[head]; // i
for (int c = 0; c < 26; c++) {
int v = ch[u][c]; // i+1
if (!v) { ch[u][c] = ch[fail[u]][c]; continue; }
q[++tail] = v;
int p = fail[u]; // j
while (p && !ch[p][c]) p = fail[p];
fail[v] = ch[p][c]; // fail[i+1] = (P[i] == P[j]) ? j+1 : 0;
last[v] = val[fail[v]] ? fail[v] : last[fail[v]]; // 以u节点作为后缀能匹配的最长的模式串(不包含u自身)
cnt[v] = 0;
}
}
}
void find(char *T) {
getfail();
for (int i = 0, j = 0; T[i]; i++) {
int c = id(T[i]);
j = ch[j][c];
if (val[j]) cnt[j]++;
else if (last[j]) cnt[last[j]]++;
}
getcnt();
}
// 这部分可用dfs实现,但是速度为N*M(N为文本串长度,M为模式串最大长度),以下利用拓扑序可以maxnode时间下完成
void getcnt() {
for (int i = tail; i >= 0; i--) { // 通过反向遍历拓扑序,完成cnt信息向last元的信息转移
int u = q[i];
cnt[last[u]] += cnt[u];
}
for (int i = 0; i < sz; i++) if (val[i]) ans[val[i]] = cnt[i];
}
}ac;
后缀数组
UVA - 11107 - Life Forms - 多文本串查找最大公共(>n/2)模式串,HDU - 6704 - K-th occurrence - 后缀数组RMQ+二分+可持久化线段树
后缀数组sa[i]:表示排名为i的后缀编号,排名数组rk[i]:表示编号为i的后缀的排名,二者互为反函数,sa[rk[i]]=rk[sa[i]]=i。通过倍增的思路,每次求解每个后缀的前缀前缀长度为的排名数组,当时,。
利用字符串的序关系可以拆分的性质(可以基数排序):如果要比较字符串的大小关系,取前缀长度,则只需比较二元组,所以可以通过倍增将字符串的比较转化为对和(表示将数组中的每个元素想做平移位)对应位组成的二元组进行排序。
又由于字符的值域大小有限,所以可以通过基数排序对二元组进行排序,于是可以得到时间复杂度为求解后缀数组的算法,空间大小为,分别由两个辅助数组t[],t2、一个桶c[]、后缀数组sa[]构成。
高度数组height[i]:表示排名为i和i-1的最长公共前缀(Longest Common Prefix, LCP),也就是sa[i-1],s[i]的LCP长度,用途是求出两个任意两个后缀j,k的LCP,不妨令rk[j]<rk[k],利用height[]可以转化为区间最小值问题:求height[rk[j]+1],height[rk[j]+2],...,height[rk[k]]的最小值。
求解height[]可以利用一个优美的性质:height[rk[i]] >= height[rk[i-1]]-1,注意分辨我们的height[rk[i]]是rk[i],rk[i]-1的LCP。解释也非常容易:主要利用到了后缀i-1和i只相差了开头的一位,首先考虑height[rk[i-1]],由height性质告诉我们i-1与k:=sa[rk[i-1]-1]的LCP为height[rk[i-1]],而i就是i-1去掉第一个字符后的结果,所以我们也将k去掉第一个字符得到k+1,我们发现i与k+1的LCPheight[rk[i-1]]-1一定是小于等于i与sa[rk[i]-1]的LCP的(这可以由k+1=sa[rk[i-1]-1]+1的排名一定小于等于rk[i]得到,由于k的排名小于i-1的排名,所以k+1的排名小于i的排名),所以height[rk[i]] >= height[rk[i-1]]-1。
const int maxn = 1e6 + 10;
#define resetn(A, n) memset(A, 0, sizeof(A[0]) * n) // 使用memset重置桶,速度优于for
struct SA {
char *s;
int n, sa[maxn], t[maxn*2], t2[maxn*2], c[maxn];
void init(char *T) { s = T; n = strlen(s); }
void build_sa(int m = 256) {
int i, *x = t, *y = t2;
resetn(c, m); // 重置桶
for (i = 0; i < n; i++) c[x[i] = s[i]]++; // 将rk1赋值到x并加入桶
for (i = 1; i < m; i++) c[i] += c[i-1]; // 桶排序
for (i = n-1; i >= 0; i--) sa[--c[x[i]]] = i; // 桶排序一定要反向枚举下标i,可以保证对于相同x[i],下标小的i排在前面
for (int k = 1; k < n; k <<= 1) { // 倍增排序长度k,现在x[]就是rkk
int p = 0; // 当前第二关键字的排名p,接下来构造y[i]为第二关键字的第i大的编号(第二关键字的sa数组)
for (i = n-1; i >= n-k; i--) y[p++] = i; // 将rkk向左平移k个后,右端空位的排名从大到小,处理第二关键字在rkk[n,...,n+k)的排名编号(因为前缀完全相同的字符,如果长度更短,则排名应该更靠前,而更短的前缀对应第二关键则的位置更靠右,所以排名是从大到小进行,以aaaa为例解释)
for (i = 0; i < n; i++) if (sa[i] >= k) y[p++] = sa[i] - k; // 将sa[i]向左平移k后即可得到第二关键字在rkk[k...n)的排名编号
resetn(c, m); // 重置桶
for (i = 0; i < n; i++) c[x[i]]++; // 将第一关键字加入桶
for (i = 1; i < m; i++) c[i] += c[i-1]; // 桶排序
for (i = n-1; i >= 0; i--) sa[--c[x[y[i]]]] = y[i]; // 首先按照第一关键字x[]排序,如果x相同,则第二关键字小的排在前面,获得rk_2k的sa数组
swap(x, y); // 交换指针,用y表示rkk,接下来构造x[]为rk_2k,难点就在于要去重
p = 1; x[sa[0]] = 0; // p为当前去重后的排名,第一个元素的排名一定是0
for (i = 1; i < n; i++) // 后续元素的值与前一个元素值判断是否相同,若相同则沿用之前的排名
x[sa[i]] = (y[sa[i]] == y[sa[i-1]] && y[sa[i]+k] == y[sa[i-1]+k]) ? p-1 : p++; // 利用rk[sa[i]]=i',只不过后面的排名中的i'是经过去重后的,
if (p == n) break; // 如果排名两两不重,则说明第一关键字已经完全区分所有后缀了,也就是所有后缀的2k长度的前缀就可以将他们完全区分开了
m = p; // 新的x[]的值域就是当前去重后的排名总数
}
}
int rank[maxn], height[maxn];
void get_height() {
for (int i = 0; i < n; i++) rank[sa[i]] = i; // 利用rk与sa互逆
for (int i = 0, k = 0; i < n; i++) { // 根据逐一构建height[rk[i]]:排名为rk[i]的高度(rk[i]和rk[i]-1的LCP)
if (k) k--; // 根据height[rk[i]]>=height[rk[i]-1]-1的性质
if (rank[i]) { // 如果rank[i]不是0
int j = sa[rank[i]-1]; // 利用sa[]找到排名为rk[i]-1的后缀编号
while (s[i+k] == s[j+k]) k++; // 若前缀相同继续增加高度
}
height[rank[i]] = k;
}
}
}sa;ababa aabaaaab aaaa // 三个例子
sa: 5 3 1 4 2 sa: 4 5 6 1 7 2 8 3 sa: 4 3 2 1
height sorted height sorted height sorted
0 a 0 aaaab 0 a
1 aba 3 aaab 1 aa
3 ababa 2 aab 2 aaa
0 ba 3 aabaaaab 3 aaaa
2 baba 1 ab
2 abaaaab
0 b
1 baaaab Hash
将字符串后缀以 进制的形式表示出来的值称为Hash值,例如12345在 进制下每一位的Hash值就是(下标从 开始):
也就是说 ,取出以 开头长度为 的 ,我们可以通过以下方法判断子串是否相同:
其实并非必须要用后缀来表示Hash值,也可以类似地用前缀表示Hash值。
typedef unsigned long long ULL; // 使用自然溢出
struct StrHash {
ULL n, H[maxn], xp[maxn], x = 2027; // xp表示x^power,x为进制数
StrHash() { xp[0] = 1; for (int i = 1; i < maxn; i++) xp[i] = xp[i-1] * x; }
void init(char *s) { // 初始化字符串s的hash数组: H
n = strlen(s); H[n] = 0;
for (int i = n-1; i >= 0; i--) H[i] = H[i+1] * x + s[i];
}
ULL hash(int l, int r) { return H[l] - H[r+1] * xp[r-l+1]; } // 获取s[l,...,r]的hash值
}shash;
char s[maxn];
int rank[maxn], hash[maxn]; // 这两个变量名都和std重名了,需要删掉using namespace std;
int check(int L) { // 判断字符串s中长度为L的子串的最大出现次数
int mx = 0, tot = 0;
for (int i = 0; i < n-L+1; i++) {
rank[i] = i;
hash[i] = shash.hash(i, i + L - 1);
}
std::sort(rank, rank+n-L+1, [](int &a, int &b){ return hash[a] == hash[b] ? a < b : hash[a] < hash[b]; }); // lambda函数,获得排序后的hash值下标: rank数组
for (int i = 0; i < n-L+1; i++) {
if (i == 0 || hash[rank[i]] != hash[rank[i-1]]) tot = 0; // 判断相邻的hash是否一样就可以得到有多少个长度为L的相同的子串个数
mx = std::max(mx, ++tot);
}
return mx;
}
Manacher
Manacher算法用于求解最大回文串长度,方法也是DP,思路与KMP相似,避免使用已访问过的字符,从而达到线性复杂度,首先由于回文串有奇偶问题,如果原串长度为,则进行以下填补,使得最后得到的串长度为:
\text{原串}:12212321\\ \text{填补后}:$\#1\#2\#2\#1\#2\#3\#2\#1\# \text{}
| T | $ | # | 1 | # | 2 | # | 2 | # | 1 | # | 2 | # | 3 | # | 2 | # | 1 | # |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| f | 1 | 1 | 2 | 1 | 2 | 5 | 2 | 1 | 4 | 1 | 2 | 1 | 6 | 1 | 2 | 1 | 2 | 1 |
设 表示填补后的串 ,以 为回文中心的最大回文串半径(半径包括回文中心),不难发现,原串的对应位置 处的原最大回文串长度就是 ,可以理解为将所有左侧的字符向右移一位,填补#的位置,并删去左侧最左端的#,即可得到原最大回文串长度。
假设当前的最大回文串右端点为 ,对应的回文中心为 ,考虑当前要求解的 ,设 关于 的对称点为 ,于是可分以下几个情况(思路就是最大化利用 的回文串长度):
-
当 时,
-
,则 。
-
,则 。
-
-
当 时,。
所以可以通过 的值对 进行下界估计,然后再向右尝试对 进行延拓:
const int maxn = 1e5 + 10;
struct Manacher {
char s[maxn<<1];
int n, f[maxn<<1];
void init(char *T) {
n = 0;
s[n++] = '$'; s[n++] = '#';
for (int i = 0; T[i]; i++) s[n++] = T[i], s[n++] = '#';
}
void build() {
int c = 0, r = 0; // 当前最大右端点回文串为r-1,该最大回文串中心为c,满足c+f[c] = r
for (int i = 0; i < n; i++) {
int &p = f[i];
p = r > i ? std::min(f[2*c-i], r-i) : 1; // 如果i在当前最大回文串内,则先利用对称点的长度
while (s[i-p] == s[i+p]) p++;
if (i + p > r) r = i + p, c = i; // 如果当前右端点大于r,则当前串成为最大右端点回文串
}
}
}mc;后缀自动机
定义:设 为SAM中的节点,用 表示节点 对应的字符串集合, 为所有字符串集合中最长的字符串长度,用 表示节点 对应的 集合, 表示节点 向字符 在DAG图上的边, 为节点 的后缀链接。
引理1:定义一下等价关系 ,则 有 。
引理2:记 ,则 ,且在后缀链接树中 的子节点两两不交,即(集合的不交并 记为 )
引理3:从SAM中的起点沿DAG边达到 的左右路径对应的字符串,构成 ,即 ,则 ( 表示将 中的每个字符串后缀都加上字符 ),且 。
template<const int maxn> // SAM数组大小,开成加入的最大字符串长度两倍
struct SuffixAutomaton {
std::map<char, int> next[maxn]; // DAG图,如果字典序较少建议用数组
int link[maxn], len[maxn], sz, last; // link为后缀链接边,len为节点对应的而字符串集合中最大长度,sz为SAM中节点数,last为最后加入的一个节点
void init() { sz = 0; last = new_node(); } // 初始化SAM,将0号节点作为空串集合
int new_node() { // 创建新节点,重置上面所有的参数
link[sz] = -1; len[sz] = 0;
next[sz].clear();
return sz++;
}
void insert(char c) { // 增量构建,加入新字符c
int p = last, cur = new_node(); // 在当前节点last后创建新节点
len[last = cur] = len[p] + 1; // 最大长度为当前串长度
while (p != -1 && !next[p].count(c)) next[p][c] = cur, p = link[p]; // 将与p相同后缀的节点全部加上当前字符c
if (p == -1) { link[cur] = 0; return; } // 若到达根节点,说明当前加入的所有后缀均为第一次出现
int q = next[p][c]; // 转到之前出现过的后缀对应的节点
if (len[p] + 1 == len[q]) { link[cur] = q; return; } // 如果该节点中所有字符串均为串的后缀,则直接加入其中即可
int nq = new_node(); // 否则需要将q中是当前后缀的一部分(长度<=len[p]+1的字符串)取出来放到新节点nq中
next[nq] = next[q]; // nq作为q后缀的子集,原本DAG途中的边仍然继承
link[nq] = link[q], len[nq] = len[p] + 1, link[q] = link[cur] = nq; // 在后缀链接树上看,nq就是q和link[q]之间加入的新节点,并且其包含的字符串个数正好就是len[p]+1 - link[q]
while (p != -1 && next[p][c] == q) next[p][c] = nq, p = link[p]; // 将原本DAG以p中字符串为后缀链接到q的边都转移到nq中,也就是删去q中长度<=len[p]+1的全部字符串
}
void build(char *s) { while (*s) insert(*s++); } // 用增量法构建SAM
};桶排序
对len数组进行从小到大排序,得到的即是DAG图的拓扑序,也是后缀链接树的深度从小到大的DFS序(用于求解endpos大小和在DAG图上进行DP都非常好用):
int c[maxn], la[maxn]; // 与SA基数排序相同,c[]为桶,la为len array,从rk值对应到id
void toposort() {
resetn(c, 0, sz);
for (int i = 0; i < sz; i++) c[len[i]]++;
for (int i = 1; i < sz; i++) c[i] += c[i-1]; // 由于len[i]的值域范围一定小于sz,所以可以将sz作为桶大小
for (int i = sz-1; i >= 0; i--) la[--c[len[i]]] = i; // sz为桶大小
for (int i = 1; i < sz; i++) endpos[la[i]] += endpos[link[la[i]]]; // 计算endpos集合大小,endpos在insert函数插入新节点时初始化为1广义SAM
HDU - 4436 - str2int - E3 - 广义SAM模板题(只用到DAG图)
广义SAM,就是一个SAM中同时插入多个字符串,其实方法很简单,只需在每次插入新串前重置last = 0,插入串的字符c时,判断是否当前插入的节点已经在SAM中有对应节点,如果已有则将last直接转移过去,否则类似创建nq节点,从q节点中分裂出后缀长度小于等于len[p]+1部分的子串,除了不用将link[cur]设置为nq其他与之前完全一致,这里引入split函数,只需要对insert(char c)函数进行修改:
int split(int c, int p, int q, int cur = -1) {
int nq = new_node();
copy(next[nq], next[q]);
link[nq] = link[q]; len[nq] = len[p] + 1; link[q] = nq;
if (cur != -1) link[cur] = nq;
while (p != -1 && next[p][c] == q) next[p][c] = nq, p = link[p];
return nq;
}
void insert(char c) {
c = id(c); int p = last, np = next[p][c];
if (np) {
if (len[p]+1 == len[np]) last = np;
else last = split(c, p, np);
return;
}
int cur = new_node();
len[last = cur] = len[p] + 1;
while (p != -1 && !next[p][c]) next[p][c] = cur, p = link[p];
if (p == -1) { link[cur] = 0; return; }
int q = next[p][c];
if (len[p] + 1 == len[q]) { link[cur] = q; return; }
split(c, p, q, cur);
}倍增求子串对应的节点
为了求文本串T的某个子串T[l,...,r]在后缀链接树的节点位置,即T[l,...,r]所处的endpos节点。
方法:记录下每个字符串结束位置,例如T[0,...,r]对应的SAM节点记为pos[r],然后在后缀链接树上从pos[r]出发,在树上倍增找祖先节点u中满足len[u]>=r-l+1最浅的节点,这就可以用树上倍增解决了(类似倍增求LCA):
int jump[maxn][18]; // 倍增数组
void build_jump() {
for (int i = 0; i < sz; i++) jump[i][0] = link[i];
for (int j = 1; (1<<j) < sz; j++)
for (int i = 0; i < sz; i++)
if (jump[i][j-1] == -1) jump[i][j] = -1; // jump数组没有初始化,所以每个值都要赋值
else jump[i][j] = jump[jump[i][j-1]][j-1];
}
// 倍增求T[l,...r]的对应节点
int p = pos[r];
for (int i = 17; i >= 0; i--) { // 从大到小枚举,优先贪心长的高度
int q = jump[p][i]; if (q == -1) continue;
if (len[q] >= r-l+1) p = q;
}
// 倍增从大到小枚举是因为,假设满足条件的最浅的节点要跳的高度为0101(二进制),如果从小到大枚举那只能跳0011高度,而从大到小枚举就可以跳到0101这个高度了(贪心思想,反证证明)维护endpos集合
K-th occurrence - SAM倍增 + 线段树合并
有些题目需要实际维护endpos集合,比如求出某个节点的endpos集合中第k大的元素(就是该节点对应的字符串集合在原串中第k次出现的位置),我们考虑每个节点u对应一颗权值线段树(之所以称为权值线段树,是因为他直接统计每个值域的值在该节点内出现的次数),然后根据len数组从大到小的顺序(后缀链接树从深到浅),将u的线段树合并到link[u]的线段树中即可。
TNode* merge(TNode *p1, TNode *p2) { // 线段树合并,也必须用指针,因为也可能走到nullptr
if (!p1 || !p2) return p1 ? p1 : p2;
TNode &p = *new_node(p1->l, p1->r);
p.ls = merge(p1->ls, p2->ls);
p.rs = merge(p1->rs, p2->rs);
pushup(p); return &p;
}时间复杂度计算
向lnc同学请教了下总算明白了时间复杂度就是稳定的,根据上述代码,我们发现线段树合并算法满足以下性质:合并两颗线段树的时间复杂度为两颗线段树并的节点数,首先给出以下两个结论:
假设初始有颗线段树,每颗线段树的叶结点数目均为,第颗线段树的初始节点数为。
- 对于任意的一种合并方法,将颗线段树两两合并最后得到一颗线段树,其时空复杂度均为。
- 假设初始时每颗线段树都是两两不交的单点,即,则合并所有线段树的时空复杂度为。
我们证明第一个结论:只需发现,每个线段树的结构都是相同的(叶结点有个),考虑线段树上每个节点的创建次数,由于线段树合并的性质,该节点的创建次数一定不超过该节点在所有的初始线段树中的出现次数(反证法很容易证明),所以合并的时间复杂度就是,由于每一次合并都会开一个新的节点,所以时空复杂度相同。
第二个结论是第一个结论的特例,也就是基于第一问求出每个非叶子节点合并时会被创建多少次,如下图所示
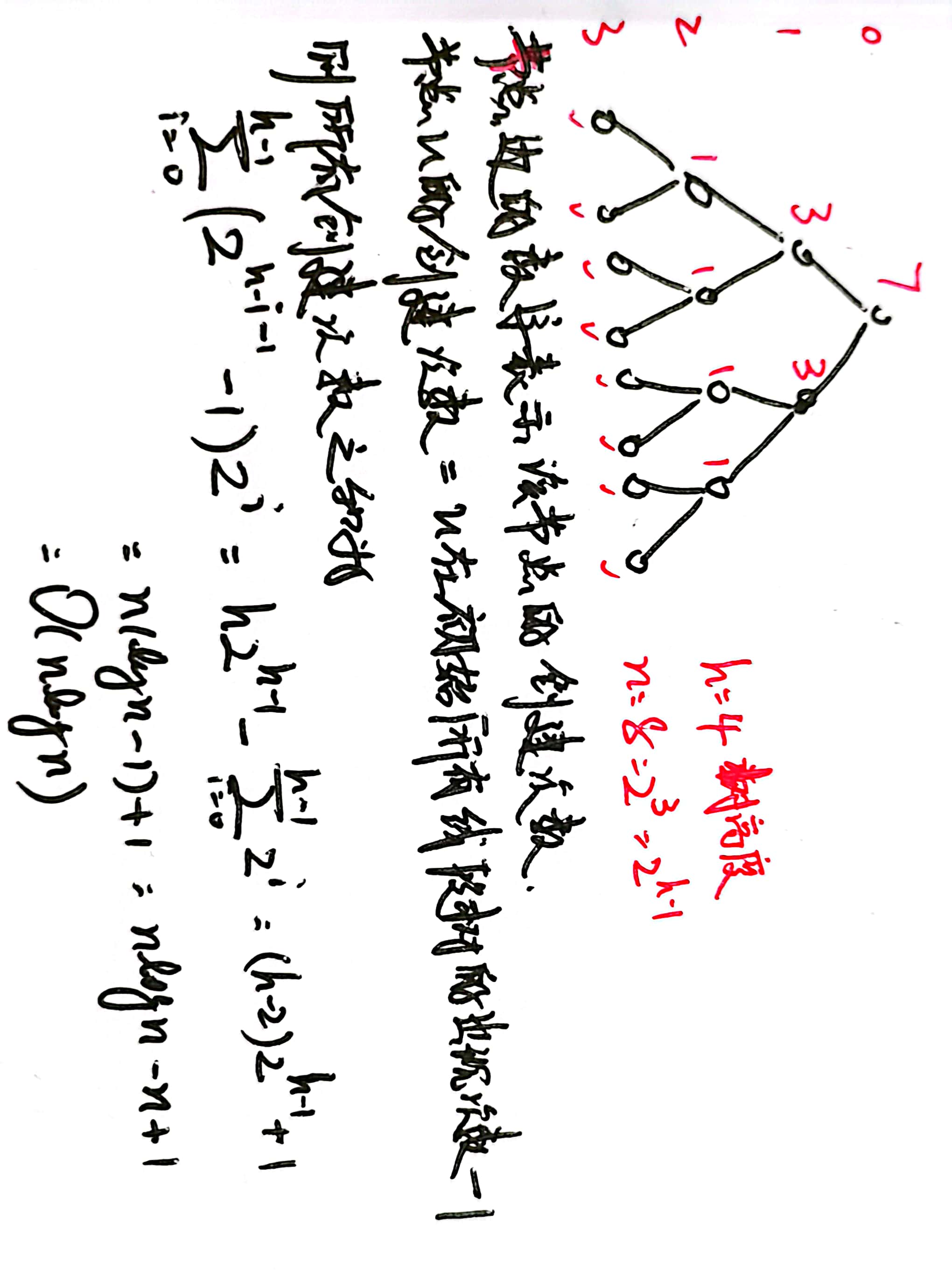
根据上述结果,我们还可以给出线段树合并的开的节点数具体应该是,为节点数目,再加上初始时的所有线段树的节点数目,于是总的节点数目应该开到,也就是,线段树大概要开到。
因为可能重复在同一个位置创建节点,将之前节点覆盖时会产生内存泄漏,所以从数组中取新的节点可以避免该问题。
struct TNode {
TNode *ls, *rs; int l, r, sum;
TNode() {}
void init(int l, int r) { this->l = l, this-> r = r; ls = rs = nullptr; sum = 0; }
void update(int k) { sum += k; }
};
template<const int maxn, const int LOGN=18>
struct SegmentTree {
TNode t[2 * maxn * LOGN];
int sz;
void init() { sz = 0; }
TNode* new_node(int l, int r) { t[sz].init(l, r); return &t[sz++]; }
void pushup(TNode &p) {
if (!p.ls || !p.rs) p.sum = p.ls ? p.ls->sum : p.rs->sum;
else p.sum = p.ls->sum + p.rs->sum;
}
void update(TNode *&p, int l, int r, int k) { // 此处p只能用指针,因为有可能是空值
if (!p) p = new_node(l, r); // 只在点不存在时进行加点
if (l == r) { p->update(1); return; }
int mid = (l+r) >> 1;
if (k <= mid) update(p->ls, l, mid, k);
else update(p->rs, mid+1, r, k);
pushup(*p);
}
TNode* merge(TNode *p1, TNode *p2) { // 线段树合并,也必须用指针,因为也可能走到nullptr
if (!p1 || !p2) return p1 ? p1 : p2;
TNode &p = *new_node(p1->l, p1->r);
p.ls = merge(p1->ls, p2->ls);
p.rs = merge(p1->rs, p2->rs);
pushup(p); return &p;
}
int query(TNode &p, int k) { // 单点查询第k小
if (p.l == p.r) return p.l;
int mid = (p.l+p.r) >> 1;
if (p.sum < k) return -1;
if (p.ls) if (p.ls->sum >= k) return query(*p.ls, k);
else k -= p.ls->sum;
return query(*p.rs, k);
}
};
// 在拓朴排序中进行线段树合并
void toposort() {
... // 对len进行桶排序
for (int i = sz-1; i >= 1; i--) {
int v = la[i], u = link[v];
rt[u] = seg.merge(rt[u], rt[v]);
}
}