《机器学习实战》第四章 训练线性模型

机器学习中的线性模型

以下内容是在《机器学习实战：基于Scikit-Learn，Keras和TensorFlow》中第四章内容基础上进行的总结.

模型原理

基本定义

我们默认向量均为列向量，用小写字符表示向量，大写字符表示矩阵.

假设训练集中总共有 $m$ 个样本，第 $i$ 个样本对应的特征和标签记为 $(\boldsymbol{x}^{(i)}, y^{(i)})$，不指定具体样本，可简记为 $(\boldsymbol{x}, y)$，对于每个样本的特征和标签有以下相关定义：

• 在不同公式中 $\boldsymbol{x}$ 的维数稍有不同，假设每个特征具有 $n$ 个属性值，每个属性值分别为 $x_1,x_2,\cdots,x_n$：
  1. $\boldsymbol{x}\in \R^{n}$，标准的特征向量，$\boldsymbol{x} = (x_1,x_2,\cdots,x_n)^T$.
  2. $\boldsymbol{x}\in \R^{n+1}$，增加偏置项的特征向量，$\boldsymbol{x} = (1,x_1,\cdots, x_n)^T$，为了简化公式所用.
     上述中两种记法会在公式下方进行说明，若不加说明，则默认使用第一种记法.
• 在不同问题中标签的性质有所不同：
  1. 回归问题中 $y\in \R$；
  2. 二分类问题中 $y\in \{0, 1\}$；
  3. 多分类问题中 $\boldsymbol{y}\in \{0, 1\}^K$，其中 $K$ 表示分类类别的总数目，$\boldsymbol{y}$ 是对应类别的one-hot向量.

one-hot向量：以$K=5$为例，类别为 $3$，则该类别对应的one-hot向量为 $[0\ 0\ 0\ 1\ 0]^T$（类别从 $0$ 开始编号）.

以下符号名称具有特别的含义：

• $\hat{y}$ 表示模型预测的结果.
• $\theta$ 表示模型中包含的参数.
• $\mathcal{L}(y;\boldsymbol{x},\theta)$ 表示损失函数，简写为 $\mathcal{L}(\theta)$，书上记为 $c(\theta)$.
• $\mathcal{J}(y;\boldsymbol{x}, \theta)$ 表示成本函数，也称风险函数，简记为 $\mathcal{J}(\theta)$.
• 下文中函数对向量或者矩阵求偏导，使用的均为分母布局，即求导结果的维数和求导对象的维数相同.
  例如，$\boldsymbol{\theta} = (\theta_1,\theta_2,\cdots,\theta_n)^T\in\R^n$，函数$\mathcal{J}(\boldsymbol{\theta}):\R^n\to \R$，则

  $$\frac{\partial \mathcal{J}(\boldsymbol{\theta})}{\partial \boldsymbol{\theta}} = \left(\frac{\partial \mathcal{J}}{\partial \theta_1}, \frac{\partial \mathcal{J}}{\partial \theta_2}, \cdots, \frac{\partial \mathcal{J}}{\partial \theta_n} \right)^T$$

• 上式还可记为 $\nabla_{\boldsymbol{\theta}}\mathcal{J}(\boldsymbol{\theta})$，表示 $\mathcal{J}(\boldsymbol{\theta})$ 对向量 $\boldsymbol{\theta}$ 求梯度.

关于更多向量或矩阵导数内容，可以参考The matrix cookbook中Derivatives篇章.

1.线性回归

标签 $\boldsymbol{y}\in \R$ 为数值常量，令参数向量 $\boldsymbol{\theta} = (\theta_0,\theta_1,\cdots,\theta_n)^T$，则线性模型预测值为

$$\hat{y} = \theta_0+\theta_1x_1+\theta_2x_2+\cdots+\theta_nx_n = \boldsymbol{\theta}^T\boldsymbol{x}$$

此处的 $\boldsymbol{x}$ 为增加偏置项的特征向量.

MSE损失函数

线性回归中常用均方误差(Mean square error, MSE)作为损失函数，MSE与其对应的成本函数定义如下：

$$\mathcal{L}(\boldsymbol{\theta}) = (\boldsymbol{\theta}^T\boldsymbol{x} - y)^2,\qquad \mathcal{J}(\boldsymbol{\theta}) = MSE(\boldsymbol{\theta})= \frac{1}{m}\sum_{i=1}^m(\boldsymbol{\theta}^T\boldsymbol{x} - y)^2$$

通过标准方程求闭解

我们将全部的特征和标签分别表示为特征矩阵和标签向量的形式：

$$\boldsymbol{X} = \left[\begin{matrix} 1&x^{(1)}_1&x^{(1)}_2&\cdots&x^{(1)}_n\\ 1&x^{(2)}_1&x^{(2)}_2&\cdots&x^{(2)}_n\\ \vdots&\ddots&\vdots&\vdots\\ 1&x^{(m)}_1&x^{(m)}_2&\cdots&x^{(m)}_n\\ \end{matrix}\right],\qquad \boldsymbol{y} = \left[\begin{matrix} y^{(1)}\\ y^{(2)}\\ \vdots\\ y^{(m)} \end{matrix}\right]$$

于是MSE成本函数又可以表示为以下形式：

$$MSE(\theta) = \frac{1}{m}(\boldsymbol{X}\boldsymbol{\theta}-\boldsymbol{y})^{T}(\boldsymbol{X}\boldsymbol{\theta}-\boldsymbol{y})$$

对 $\boldsymbol{\theta}$ 求导可以得到：

$$\frac{\partial MSE(\boldsymbol{\theta})}{\partial \boldsymbol{\theta}} = \frac{2}{m}\boldsymbol{X}^T(\boldsymbol{X}\boldsymbol{\theta}-\boldsymbol{y})$$

令导数等于 $\boldsymbol{0}$ 可得

$$\hat{\boldsymbol{\theta}} = (\boldsymbol{X}^T\boldsymbol{X})^{-1}\boldsymbol{X}^T\boldsymbol{y}\tag{1.1}$$

由于 $\frac{\partial MSE(\boldsymbol{\theta})}{\partial \boldsymbol{\theta}\partial \boldsymbol{\theta}^T} = \boldsymbol{X}\boldsymbol{X}^T$ 矩阵范数恒 $\geqslant 0$（这里的矩阵范数可以是任意一种），于是 $MSE(\boldsymbol{\theta})$ 是关于 $\boldsymbol{\theta}$ 的凸函数，所以 $(1.1)$ 式得到的 $\hat{\boldsymbol{\theta}}$ 就是使成本函数最小的 $\boldsymbol{\theta}$ 值.

注意：$\boldsymbol{X}^T\boldsymbol{X}$ 不一定满秩，所以可以不存在逆矩阵，但是可以通过SVD分解得到伪逆 $X^+$（Moore-Penrose逆矩阵）代替 $(\boldsymbol{X}^T\boldsymbol{X})^{-1}\boldsymbol{X}^T$.

求解逆矩阵的时间复杂度一般为 $\mathcal{O}(n^{2.4})$ 到 $\mathcal{O}(n^3)$，而Scikit-Learn中的SVD分解复杂度约为 $\mathcal{O}(n^2)$. 不适合用于处理特征数目较大的情形.

梯度下降

成本函数对 $\boldsymbol{\theta}$ 的每一维的偏导数为：

$$\frac{\partial MSE(\boldsymbol{\theta})}{\partial \theta_j} = \frac{2}{m}\sum_{i=1}^m(\hat{y}^{(i)}-y^{(i)})x_{j}^{(i)}\tag{1.2}$$

其中 $\hat{y}^{(i)} = \boldsymbol{\theta}^T\boldsymbol{x}^{(i)}$. 记为梯度向量的形式可以如下表示：

$$\nabla_{\boldsymbol{\theta}}MSE(\boldsymbol{\theta}) = \frac{2}{m}\boldsymbol{X}^T(\boldsymbol{X}\boldsymbol{\theta}-\boldsymbol{y})$$

如果我们以 $\nabla_{\boldsymbol{\theta}}MSE(\boldsymbol{\theta})$ 作为每次的下降方向，设学习率为 $\eta$，则参数 $\boldsymbol{\theta}$ 的更新方法为如下形式：

$$\boldsymbol{\theta}^{(\text{下一步})} = \boldsymbol{\theta} - \eta\nabla_{\boldsymbol{\theta}}MSE(\boldsymbol{\theta})$$

梯度下降法分为三种，批量梯度下降，随机梯度下降，小批量梯度下降，三者的区别仅在每次计算梯度使用的训练集大小上：

• 批量梯度下降(BGD)：每次以整个训练集计算一次梯度，对参数进行更新.
• 随机梯度下降(SGD)：每次从训练集中随机选取一个样本计算梯度，对参数进行更新.
• 小批量梯度下降(Mini-BGD)：设定一个 batch_size 大小，以 batch_size 大小对以打乱的训练集划分为多个 batch，每次取一个 batch 中的样本计算一次梯度，对参数进行更新.（好处：可以利用GPU并行运算加快更新速度）

注意：使用梯度下降法必须对样本特征的属性值大小比例近似，为了避免数值较大的属性值产生“狭长的山谷”，从而减缓训练速度. 所以需要进行归一化或者标准化处理（特征缩放）.

总结

算法	$m$ 很大	$n$ 很大	并行计算	超参数	要求缩放	Scikit-Learn API
标准方程	快	慢	否	0	否	N/A
SVD	快	慢	否	0	否	LinearRegression
BGD	慢	快	否	2	是	SGDRegressor
SGD	快	快	是	$\geqslant 2$	是	SGDRegressor
Mini-BGD	快	快	是	$\geqslant 2$	是	SGDRegressor

2.多项式回归

注意：这不是多项式插值.

首先考虑特征的属性值只有一个的情况，在线性插值中，我们的模型预测值为 $\hat{y} = \theta_0 + \theta_1x$，而在 $d$ 次的多项式回归中，预测模型转化为

$$\hat{y}= \theta_0+\theta_1x+\theta_2x^2+\cdots\theta_dx^d$$

相当于在原有属性 $x$ 的基础上扩充进新的属性值 $x^2,\, x^3,\, \cdots,\, x^d$.

当属性值个数为 $n=2$ 的时候，$d=3$ 次多项式回归，需要考虑不同属性之间的组合，所以全部属性值为 $x_1^3,\, x_1^2x_2,\, x_1x_2^2,\, x_2^3,\ x_1^2,\, x_1x_2,\, x_2^2,\, x_1,\, x_2,\, 1$，总共 $10 = \binom{2+3}{2}$ 个.

类似地，当 $n=3,\ d=2$ 时，全部属性值为 $x_1^2, x_1x_2, x_1x_3, x_2^2, x_2x_3, x_3^2, x_1, x_2, x_3, 1$，总共 $10 = \binom{3+2}{3}$ 个.

可以证明，当特征属性个数为 $n$，最高幂次为 $d$ 的多项式回归中，最终扩充得到的属性值有 $\binom{n+d}{n}=\frac{(n+d)!}{n!d!}$ 个.

求解多项式扩充得到的属性值个数

首先考虑 $n$ 个属性值时，齐次为 $m$ 次的组合总共有多少，我们可以将问题转化为小球染色问题：总共有 $m$ 个球，染上 $n$ 中颜色，可以有颜色一次都不用.

该问题，就是可以有空位的隔板法，总共有 $n-1$ 个隔板，隔出来 $n$ 个空间，每个空间中的小球个数表示顺次表示每个属性值的幂次，由于可以有空位，所以先补上 $n$ 个小球，然后转化为没有空位的隔板法，所以总共有 $\binom{m+n-1}{n-1}$ 中组合.

然后对于 $d$ 次多项式回归，包含从 $0\sim d$ 次的全部齐次项，所以总共有

$$\sum_{m=0}^d\binom{m+n-1}{n-1} = \binom{d+n}{n} = \frac{(n+d)!}{n!d!}$$

上述第一个等号使用了 曲棍球恒等式(Hockey Stick Identity)，证明思路：每次固定选取一个元素，然后在选取集合中选取剩余的元素，并依次递增选取集合.

正则化线性模型

在原有线性模型基础上加入不同的正则化项即可得到不同的正则化模型，记 $\boldsymbol{w} = (\theta_1,\theta_2,\cdots,\theta_n)^T$（不包含偏置项）， 以下三种正则化模型分别对应 $\boldsymbol{w}$ 的 $l_2$范数，$l_1$ 范数和他们的线性组合.

正则化算法	正则化项
岭回归(Ridge)	$l_2$ 范数，$\frac{1}{2}\sum_{i=1}^n\theta_i^2=\frac{1}{2}|\boldsymbol{w}|_2^2$
Lasso回归	$l_1$ 范数，$\sum_{i=1}^n|\theta_i| = |\boldsymbol{w}|_1$
弹性网络	$l_1,l_2$ 范数的线性组合，$r|\boldsymbol{w}|_1+\frac{1-r}{2}|\boldsymbol{w}|_2^2$

在正则化项前的系数 $\alpha$ 称为正则化系数，用来控制模型正则化程度.

由于正则化线性模型对特征的缩放敏感，规模较大的特征值可能导致对应的参数值较大，所以正则化项同样较大，对特征缩放敏感. 故正则化模型大多都需要特征缩放.

岭回归

岭回归的成本函数为

$$\mathcal{J}(\boldsymbol{\theta}) = MSE(\boldsymbol{\theta}) + \alpha\frac{1}{2}\sum_{i=1}^n\theta_i^2 = MSE(\boldsymbol{\theta}) + \frac{\alpha}{2}||\boldsymbol{w}||_2^2$$

求解岭回归的梯度值，从而可以使用梯度下降法进行求解：

$$\nabla_{\boldsymbol{\theta}}\mathcal{J}(\boldsymbol{\theta}) = \nabla_{\boldsymbol{\theta}}MSE(\boldsymbol{\theta}) + \alpha \boldsymbol{w}$$

同样可以求解岭回归的闭解：

$$\hat{\boldsymbol{\theta}} = (\boldsymbol{X}^T\boldsymbol{X}+\alpha\boldsymbol{A})^{-1}\boldsymbol{X}^T\boldsymbol{y}\tag{2.1}$$

其中 $\boldsymbol{A} = \left[\begin{matrix} 0&0&\cdots&0\\ 0&1&\cdots&0\\ \vdots&\vdots&\ddots&\vdots\\ 0&0&\cdots&1 \end{matrix}\right]$ 为左上角为 $0$ 的 $(n+1)\times (n+1)$ 单位阵.

Lasso回归

Lasso回归的成本函数为

$$\mathcal{J}(\boldsymbol{\theta}) = MSE(\boldsymbol{\theta}) + \alpha\sum_{i=1}^n|\theta_i| = MSE(\boldsymbol{\theta}) + \alpha ||\boldsymbol{w}||_1$$

Lasso回归与岭回归的区别：由于 $l_1$ 范数对较小的的抑制比 $l_2$ 范数更强，所以Lasso回归更倾向于完全消除掉最不重要的特征的权重（也就是将它们置为0）.

由于绝对值函数 $|w|$ 的导数在 $0$ 处并不存在，但是可以用广义导数的来定义，在广义函数意义下有 $|x|' = \text{sign}(x)$，其中 $\text{sign}(x) = \begin{cases} -1,&\quad x < 0,\\ 0,&\quad x = 0,\\ 1,&\quad x > 0.\end{cases}$

|x| 的广义微分求解

设 $f(x) = |x| = \begin{cases}-x,&\quad x < 0,\\ x,&\quad x > 0.\end{cases}$，对任意的试验函数 $\varphi\in \mathcal{D}(\R)$，有

$$\begin{aligned} \langle f',\varphi\rangle =&\ -\langle f,\varphi'\rangle = -\int_{\R}f\varphi'\,\textrm{d} x = -\int_0^\infty x\varphi'\,\textrm{d}x+\int_{-\infty}^0 x\varphi'\,\textrm{d}x\\ =&\ \int_0^\infty\varphi\,\textrm{d}x - \int_{-\infty}^0\varphi\,\textrm{d}x = \langle H(x)-H(-x),\varphi\rangle = \langle \text{sign}(x),\varphi\rangle \end{aligned}$$

所以在广义函数意义下，有 $|x|' = \text{sign}(x)$.

所以Lasso回归的梯度为：

$$\nabla_{\boldsymbol{\theta}}\mathcal{J}(\boldsymbol{\theta}) = \nabla_{\boldsymbol{\theta}}MSE(\boldsymbol{\theta}) + \alpha\left[\begin{matrix}0\\\text{sign}(\theta_1)\\\text{sign}(\theta_2)\\\vdots\\\text{sign}(\theta_n)\\\end{matrix}\right]$$

由于 $\text{sign}$ 的逆函数无法求得，所以Lasso没有的闭解式.

注意：由于Lasso回归的梯度中存在 \sign 函数，导致梯度的范数大小总是较大，所以可能导致在最优解附近反弹，因此需要逐渐降低学习率 $\eta$，使得算法收敛.

弹性网络

弹性网络的成本函数为

$$\mathcal{J}(\boldsymbol{\theta}) = MSE(\boldsymbol{\theta}) + r\alpha||\boldsymbol{\theta}||_1 + \frac{1-r}{2}\alpha||\boldsymbol{\theta}||_2^2$$

其中 $r$ 称为混合比.

• 当 $r=0$ 时，弹性网络等价于岭回归.
• 当 $r=1$ 时，弹性网络等价于Lasso回归.

总结

正则化有总比没有强，避免使用纯线性回归. 岭回归作为默认选择，当实际用到的特征数目较少，可以倾向于Lasso回归或者弹性网络，因为它们会将无用的特征权重降为 $0$.

一般来说，弹性网络优于Lasso回归，因为当特征数量超过训练集大小，或者几个特征强相关时（梯度范数一直较大），Lasso回归可能非常不稳定（发散）.

3.Logistic回归

Logistic回归是在线性回归模型的基础上，加入了Logistic函数，从而将模型的输出值转化为概率分布，从而用于解决二分类问题的一种模型. 我们将标签为 $1$ 的样本称为正例，标签为 $0$ 的样本称为负例.

下文中的 $\boldsymbol{x}$ 都是增加偏置项后的特征向量.

记logistic函数为 $\sigma(\cdot)$，也称为sigmoid（S型函数），定义式如下

$$logistic(t) = \sigma(t) = \frac{1}{1+e^{-t}}$$

记线性模型的输出为得分 $t$，则对正例的估计概率 $P(y=1|\boldsymbol{x},\boldsymbol{\theta})$ 为

$$\hat{p} = \sigma(t) = \sigma(\boldsymbol{\theta}^T\boldsymbol{x})$$

模型预测值为

$$\hat{y} = \begin{cases}0,&\quad \hat{p} < 0.5\text{ 或 }t < 0,\\ 1,&\quad \hat{p} \geqslant 0.5\text{ 或 } t \geqslant 0.\end{cases}$$

一般将模型输出的分数 $t$ 记为logit原因：由于 $\sigma(t) = \hat{p}$，而 $\sigma$ 的反函数正好是对数几率(log odds)，即（可以通过代入验证下式成立）

$$\sigma^{-1}(p) = logistic^{-1}(p) = logit(p) = \log\left(\frac{p}{1-p}\right) = t$$

对数几率logit：正类别的估计概率与负类别的估计概率之比的对数.

单个训练样本的logistic回归成本函数定义如下（负估计概率的对数似然）

$$\mathcal{J}(\boldsymbol{\theta}) = \begin{cases}-\log(\hat{p}),&\quad y=1,\\ -\log(1-\hat{p}),&\quad y=0.\end{cases}$$

logistic回归的成本函数为

$$\mathcal{J}(\boldsymbol{\theta}) = -\frac{1}{m}\sum_{i=1}^m\left[y^{(i)}\log(\hat{p}^{(i)})+(1-y^{(i)})\log(1-\hat{p}^{(i)})\right]$$

上述成本函数是通过将后验概率 $\hat{y}$ 作为 $y=1$ 的估计，使用对数极大似然法求解得到的，证明可见下文.

---

由于我们用 $\hat{p}$ 作为后验概率估计，即 $P(y=1|\boldsymbol{x},\boldsymbol{\theta}) = \hat{p}$，则 $P(y=1|\boldsymbol{x},\boldsymbol{\theta}) = 1-\hat{p}$，于是大小为 $m$ 的训练集对应的对数似然为

$$l(\boldsymbol{\theta}) = \sum_{i=1}^m\log P(y^{(i)}|\boldsymbol{x^{(i)}},\boldsymbol{\theta})\tag{3.1}$$

下面我们以一个样本为例，分析对数似然函数，由于 $y\in\{0,1\}$，则

$$P(y|\boldsymbol{x},\boldsymbol{\theta}) = yP(y=1|\boldsymbol{x},\boldsymbol{\theta}) + (1-y)P(y=0|\boldsymbol{x},\boldsymbol{\theta}) = y\hat{p} + (1-y)(1-\hat{p})$$

代入表达式 $y = \frac{e^{t}}{1+e^{t}}$ 可得 $P(y|\boldsymbol{x},\boldsymbol{\theta}) = \frac{y\cdot e^t + (1-y)}{1+e^t}$，于是对数似然为

$$\begin{aligned}\tag{3.2} \log P(y|\boldsymbol{x},\boldsymbol{\theta}) =&\ \log(y\cdot e^t + (1-y)) - \log(1+e^t)\\ \xlongequal{y\in\{0,1\}}&\ \textcolor{red}{yt - \log(1+e^t)}\\ =&\ y\log \hat{p} - y\log (1-\hat{p}) + \log(1-\hat{p})\\ =&\ \textcolor{green}{y\log\hat{p} + (1-y)\log (1-\hat{p})} \end{aligned}$$

代回到 $(3.1)$ 式，由于需要转化为极小化问题，在前面加上负号，并对每个样本进行平均后，我们就得到了logistic回归的成本函数.

在 $(3.2)$ 式中，红色标记出来的式子便于进一步求解对 $\boldsymbol{\theta}$ 的导数，绿色式子则更容易记忆.

---

我们将使用梯度下降法对logistic成本函数进行优化，并说明该问题为凸优化问题，将 $t = \boldsymbol{\theta}^T\boldsymbol{x}$ 代入到 $(3.2)$ 式中红色式子中，可得

$$\begin{aligned} \frac{\partial}{\partial \boldsymbol{\theta}}P(y|\boldsymbol{x},\boldsymbol{\theta}) =&\ \frac{\partial}{\partial \theta}\left[y\boldsymbol{\theta}^T\boldsymbol{x}-\log(1+e^{\boldsymbol{\theta}^T\boldsymbol{x}})\right]\\ =&\ y\boldsymbol{x} - \frac{e^{\boldsymbol{\theta}^T\boldsymbol{x}}}{1+e^{\boldsymbol{\theta}^T\boldsymbol{x}}}\boldsymbol{x}\\ =&\ (y-\hat{p})\boldsymbol{x} \end{aligned}$$

所以logistic成本函数对 $\boldsymbol{\theta}$ 的梯度为

$$\frac{\partial \mathcal{J}(\boldsymbol{\theta})}{\partial \boldsymbol{\theta}} = \frac{1}{m}\sum_{i=1}^m(\hat{p}^{(i)}-y^{(i)})\boldsymbol{x^{(i)}}\tag{3.3}$$

可以发现，logistic成本函数对 $\boldsymbol{\theta}$ 的梯度与线性回归中MSE对 $\boldsymbol{\theta}$ 的梯度 $(1.2)$ 式基本相同.

---

下面我们通过证明 $\mathcal{J}(\boldsymbol{\theta})$ 的二阶偏导数非负，以证明logistic回归问题是凸优化问题，即成本函数对参数 $\boldsymbol{\theta}$ 是凸函数：

$$\begin{aligned} -\frac{\partial^2}{\partial\boldsymbol{\theta}\partial\boldsymbol{\theta}^T}\log P(y|\boldsymbol{x},\boldsymbol{\theta}) =&\ -\frac{\partial}{\partial \theta^T}\left[y\boldsymbol{x}-\frac{\boldsymbol{x}}{1+e^{-\boldsymbol{\theta}^T\boldsymbol{x}}}\right]\\ =&\ \frac{e^{-\boldsymbol{\theta}^T\boldsymbol{x}}}{(1+e^{-\boldsymbol{\theta}^T\boldsymbol{x}})^2}\boldsymbol{x}\boldsymbol{x}^T\\ =&\ \hat{p}(1-\hat{p})\boldsymbol{x}\boldsymbol{x}^T\geqslant 0 \end{aligned}$$

4.Softmax回归

我们对logistic回归进行推广到多维分类问题上，设总共有 $K$ 个类别.

在多维分类问题中，如果使用数字对样本标签进行编号，例如 $0,1,2,...,K-1$，则模型会认为标签数值靠近的样本具有类似的性质，而这往往并不正确（需要考虑到特征之间的关系），所以我们往往使用one-hot向量的方法对多类别标签进行编号.

one-hot编码，具体来说，若类别属于 $k$（从 $0$ 开始编号），则对应的one-hot向量为

$$\boldsymbol{y} = (\underbrace{0,\cdots,0}_{k\text{个}},1,\underbrace{0,\cdots, 0}_{K-k-1\text{个}})^T$$

下文中的 $\boldsymbol{x}$ 仍然是加上偏置项后的特征向量.

还是利用线性模型作为分数预测，只不过这需要预测 $k$ 个分数，所以参数向量总共会有 $k$ 个，可以表示为参数矩阵的形式 $\Theta = (\boldsymbol{\theta}^{(1)},\boldsymbol{\theta}^{(2)},\cdots,\boldsymbol{\theta}^{(K)})^T\in \R^{K\times (n+1)}$，则第 $k$ 类预测的分数为

$$t_k(\boldsymbol{x}) = (\boldsymbol{\theta}^{(k)})^T\boldsymbol{x} = [\Theta\boldsymbol{x}]_k$$

$[\Theta\boldsymbol{x}]_k$ 表示先计算出 $\Theta\boldsymbol{x}$ 的结果后，取第 $k$ 维分量.

求出每一类的得分之后，就可以通过softmax函数计算属于第 $k$ 类的概率 $\hat{p}_k$（softmax是 $\R^{K}$ 空间中的函数）

$$\hat{p}_k = \sigma(t(\boldsymbol{x}))_k = \frac{\exp(t_k(\boldsymbol{x}))}{\sum_{j=1}^K\exp(t_j(\boldsymbol{x}))}$$

logistic函数正好与softmax函数等价（将softmax预测分数向量记为 $(t, 0)^T$，其中 $t$ 是logistic回归中的分数，则softmax函数等于logistic函数），所以称softmax回归是logistic回归在多维分类下的推广. 进一步，softmax的成本函数与对参数的梯度，均与logistic类似.
所以softmax和logistic函数均用 $\sigma$ 表示，如果作用在标量上则是logistic函数，如果作用在向量上则是softmax函数.

我们将预测概率中概率最高的类别作为分类结果：

$$\hat{y} = \argmax_{k}\sigma(t(\boldsymbol{x}))_k = \argmax_{k}t_k(\boldsymbol{x}) = \argmax_{k}((\boldsymbol{\theta}^{(k)})^T\boldsymbol{x})$$

softmax的成本函数为交叉熵：

$$\mathcal{J}(\Theta) = -\frac{1}{m}\sum_{i=1}^m\sum_{k=1}^Ky_k^{(i)}log(\hat{p}_k^{(i)}) = -\frac{1}{m}\sum_{i=1}^m\log(\hat{p}_{k_i}^{(i)})$$

其中 $k_i$ 表示第 $i$ 个样本所属的类别，也就是说，对应的one-hot标签 $y^{(i)}$ 只有在 $k_i$ 维分量是 $1$ 其他均为 $0$. 上式中第二个等号只需将one-hot具体形式代入即可得到.

---

由于要使用梯度下降法对softmax成本函数进行优化，并说明该问题为凸优化问题，还是先考虑单个样本的情形，记交叉熵损失函数为 $\mathcal{L}(\Theta) = \sum_{i=1}^K\boldsymbol{y}_i\log \hat{p}_k$，为了使推导美观，不妨先令特征维数 $n=1$，并用 $\theta_k$ 表示 $\boldsymbol{\theta}^{(k)}$，则

$$\begin{aligned} \frac{\partial \mathcal{L}(\Theta)}{\partial\theta_k} =&\ \frac{\partial}{\partial \theta_k}\sum_{i=1}^Ky_i\log\frac{e^{\theta_kx}}{\sum_{j=1}^Ke^{\theta_jx}}\\ =&\ y_k\frac{\textcolor{red}{\sum_{j=1}^Ke^{\theta_jx}}}{\textcolor{green}{e^{\theta_kx}}}\frac{\textcolor{green}{e^{\theta_kx}}\sum_{j=1}^Ke^{\theta_jx}-e^{\textcolor{green}{2}\theta_kx}}{\left(\sum_{j=1}^Ke^{\theta_jx}\right)^\textcolor{red}{2}}x + \sum_{i\neq k}y_i\frac{\textcolor{red}{\sum_{j=1}^Ke^{\theta_jx}}}{\textcolor{green}{e^{\theta_ix}}}\frac{-\textcolor{green}{e^{\theta_ix}}e^{\theta_kx}}{\left(\sum_{j=1}^Ke^{\theta_jx}\right)^\textcolor{red}{2}}x\\ =&\ y_kx - y_k\frac{e^{\theta_kx}}{\sum_{j=1}^Ke^{\theta_jx}}x - \sum_{i\neq k}y_i\frac{e^{\theta_kx}}{\sum_{j=1}^Ke^{\theta_jx}} x\\ \xlongequal{\sum_{i=1}^Ky_i=1}&\ y_kx - \frac{e^{\theta_kx}}{\sum_{j=1}^Ke^{\theta_jx}} x = (y_k - \hat{p}_k)x \end{aligned}$$

对于一般的维数 $n$，类似可得参数向量的梯度为（仅需将 $x$ 从标量改为向量形式）

$$\nabla_{\boldsymbol{\theta}^{(k)}}\mathcal{L}(\Theta) = (y_k-\hat{p}_k)\boldsymbol{x}$$

建议先推导 $n=1, K=2,3$ 时的简单形式，然后类比推导一般情况下的表达式.

于是可以得到softmax成本函数对参数向量的梯度

$$\nabla_{\boldsymbol{\theta}^{(k)}}\mathcal{J}(\Theta) = \frac{1}{m}\sum_{i=1}^m(\hat{p}_k^{(i)} - y_k^{(i)})\boldsymbol{x}^{(i)}$$

可以发现，softmax成本函数对 $\boldsymbol{\theta}$ 的梯度与logistic回归梯度完全相同，与线性回归梯度基本相同，分别为 $(1.2),(3.3)$ 式.

---

通过求 $\mathcal{L}(\Theta)$ 对 $\boldsymbol{\theta}$ 的二阶导数，可以证明该softmax回归是凸优化问题：

$$\begin{aligned} -\frac{\partial \mathcal{L}(\Theta)}{\partial\boldsymbol{\theta}^{(k)}\partial\boldsymbol{\theta}^{(k)^T}} =&\ \frac{e^{\boldsymbol{\theta}^{(k)^T}\boldsymbol{x}}\left(\sum_{j=1}^ke^{\boldsymbol{\theta}^{(j)^T}\boldsymbol{x}}\right)-e^{2\boldsymbol{\theta}^{(k)^T}\boldsymbol{x}}}{\left(\sum_{j=1}^ke^{\boldsymbol{\theta}^{(j)^T}\boldsymbol{x}}\right)^2}\boldsymbol{x}\boldsymbol{x}^T\\ =&\ (\hat{p}-\hat{p}^2)\boldsymbol{x}\boldsymbol{x}^T\\ =&\ \hat{p}(1-\hat{p})\boldsymbol{x}\boldsymbol{x}^T \geqslant 0 \end{aligned}$$

代码实现

英文代码参考github - handson-ml2/04_training_linear_models.ipynb，下面内容为自己重新实现的Jupyter Notebook代码，源代码：github - 4.linear_models.ipynb. 由于重新配置过Jupyter，生成的图片主题为暗色调，配置Jupyter方法请见blog.

# Python version: 3.9.12
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
from pathlib import Path

IMAGES_PATH = Path("./figure/linear_models")  # 设置图像保存路径
IMAGES_PATH.mkdir(parents=True, exist_ok=True)  # 创建文件夹

def save_fig(fname, tight_layout=True, fig_extension='png', resolution=300):
    path = IMAGES_PATH.joinpath(fname + '.' + fig_extension)
    print(f"Save figure in '{path}'")
    if tight_layout:
        plt.tight_layout()
    plt.savefig(path, format=fig_extension, dpi=resolution)

1.线性回归

标准方程求闭解

构造出带有偏置项的特征矩阵 $X$ 后，通过闭解式得到最优的参数向量：$\hat{\boldsymbol{\theta}} = (\boldsymbol{X}^T\boldsymbol{X})^{-1}\boldsymbol{X}^T\boldsymbol{y}$.

• np.ones((n, m)) 可以创建形状为 (n, m) 全为1的矩阵.
• np.c_[a, b] 可以将矩阵 a,b 按照列进行并排放置.
• np.linalg.inv() 可以求解逆矩阵.

np.random.seed(42)
X = 2 * np.random.rand(100, 1)  # 在[0,2)之间均匀生成100个样本
np.random.seed(42)
y = 2 + 4 * X + np.random.randn(100, 1)  # 在线性函数2+4x的基础上加入高斯噪声

plt.plot(X, y, 'b.')
plt.xlabel("$x_1$")
plt.ylabel("$y$", rotation=0)
plt.axis([0, 2, 0, 12])
save_fig("generated_linear_data")
plt.show()

X_b = np.c_[np.ones((100, 1)), X]  # 对每个样本加入偏置项, x0=1
theta_best = np.linalg.inv(X_b.T @ X_b) @ X_b.T @ y
print(theta_best)  # [[2.21509616] [3.77011339]] 与创建数据所用的 2+4x 比较接近

X_line = np.array([[0], [2]])
X_line_b = np.c_[np.ones((2, 1)), X_line]
y_predict = X_line_b @ theta_best

plt.plot(X_line, y_predict, 'r-', lw=2, label='预测值')
plt.plot(X, y, 'b.')
plt.axis([0, 2, 0, 12])
plt.xlabel("$x_1$")
plt.ylabel("$y$", rotation=0)
plt.legend()
save_fig("linear_model_predictions")
plt.show()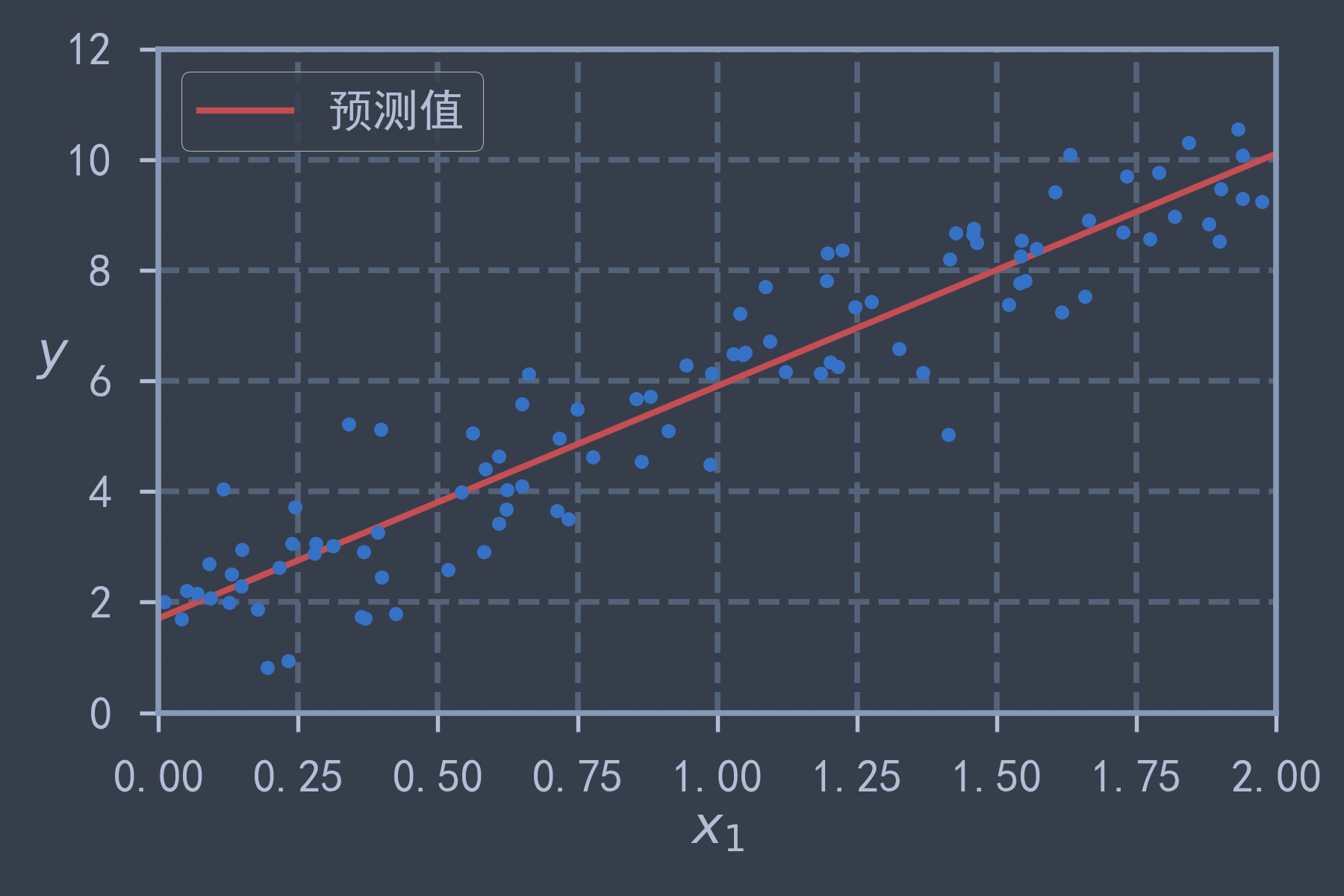

或者使用 sklearn 中的 sklearn.linear_model.LinearRegression 使用SVD分解方法求解 $\boldsymbol{X}^T\boldsymbol{X}$ 的伪逆.

通过调用 intercept_ 获得截距（偏置项），coef_ 获得系数.

而 sklearn.linear_model.LinearRegression 是基于 np.linalg.lstsq() 最小二乘函数得到的，也可通过 np.linalg.pinv() 直接计算伪逆.

from sklearn.linear_model import LinearRegression

line_reg = LinearRegression()
line_reg.fit(X, y)
print(line_reg.intercept_, line_reg.coef_)  # [2.21509616] [[3.77011339]]
theta_best_svd, residuals, rank, s = np.linalg.lstsq(X_b, y)
print(theta_best_svd)  # [[2.21509616] [3.77011339]]
print(np.linalg.pinv(X_b) @ y)  # [[2.21509616] [3.77011339]]

梯度下降

$$\nabla_{\theta_j}MSE(\boldsymbol{\theta}) = \frac{2}{m}\sum_{i=1}^m(\hat{y}^{(i)}-y^{(i)})x_{j}^{(i)} = \frac{2}{m}\boldsymbol{X}^T(\hat{\boldsymbol{y}}-\boldsymbol{y})$$

批量梯度下降(Batch Gradient Descent, BGD)

eta = 0.1  # 学习率
n_iterations = 1000  # 迭代次数
m = 100  # 训练集大小

np.random.seed(42)
theta = np.random.rand(2, 1)  # 随机初始化

for iteration in range(n_iterations):
    gradients = 2/m * X_b.T @ (X_b @ theta - y)
    theta = theta - eta * gradients
print(theta)  # [[2.21509616] [3.77011339]] 与闭解相同

theta_path_bgd = []  # 存储BGD的theta变化
def plot_gradient_descent(theta, eta, theta_path=None):
    plt.plot(X, y, 'b.')
    for iteration in range(n_iterations):
        if theta_path is not None:
            theta_path.append(theta)
        if iteration < 10:
            y_line_predict = X_line_b @ theta
            linestyle = 'r--' if iteration == 0 else 'b-'
            label = '初始状态' if iteration == 0 else None
            plt.plot(X_line, y_line_predict, linestyle, label=label)
        gradients = 2/m * X_b.T @ (X_b @ theta - y)
        theta = theta - eta * gradients
    plt.xlabel("$x_1$")
    plt.axis([0, 2, 0, 12])
    plt.title(f"$\eta={eta}$")

np.random.seed(42)
theta = np.random.rand(2, 1)
plt.figure(figsize=(12, 4))
plt.subplot(131); plot_gradient_descent(theta, eta=0.01); plt.legend()
plt.ylabel("y", rotation=0)
plt.subplot(132); plot_gradient_descent(theta, eta=0.1, theta_path=theta_path_bgd)
plt.subplot(133); plot_gradient_descent(theta, eta=0.5)
save_fig("bgd")
plt.show()  # 可以看出不同的学习率的曲线收敛速度不同，当学习率太大会导致算法发散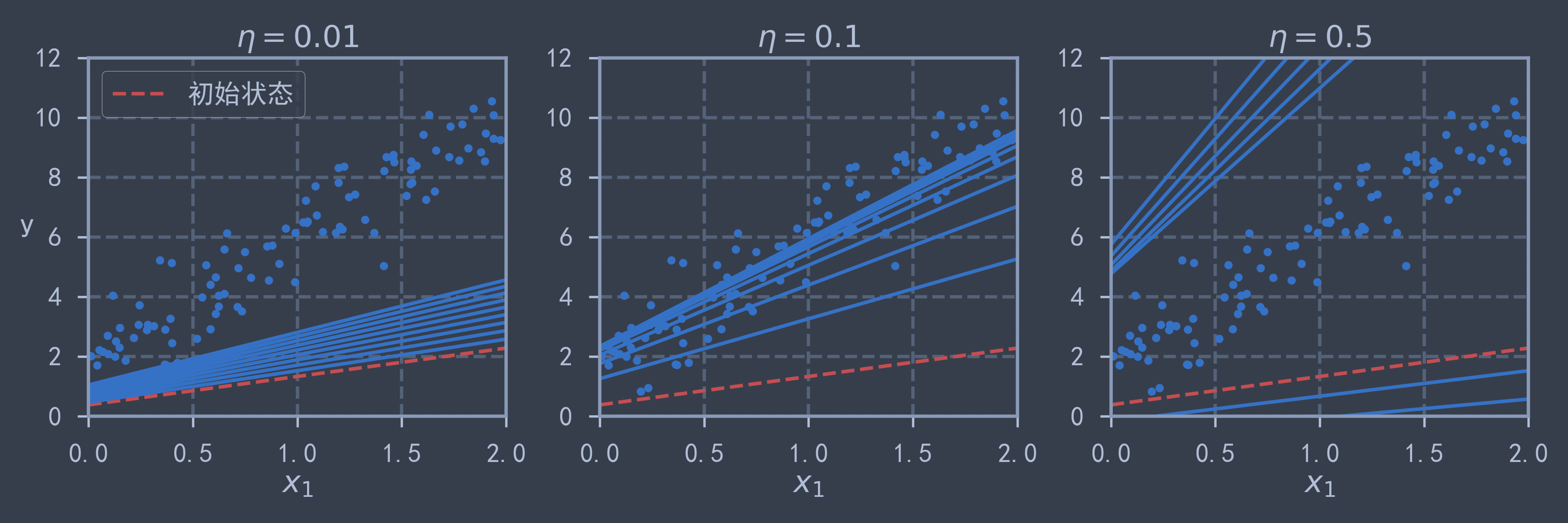

随机梯度下降(Stochastic Gradient Descent, SGD)

以一个样本计算梯度并进行更新，需要随迭代次数 $t$ 的增加逐渐降低学习率，使用以下方法计算学习率

$$\eta(t) = \frac{t_0}{t_1+t}$$

使用 sklearn.linear_model.SGDRegressor 可以便捷地达到相同的效果，其中也有学习率递降策略由 learning_rate 控制，由于未使用正则化项，所以令 penalty=None.

theta_path_sgd = []
n_epoch = 10
np.random.seed(42)
theta = np.random.rand(2, 1)
t0, t1 = 5, 50
def learning_schedule(t):
    return t0 / (t1 + t)

for epoch in range(n_epoch):
    for i in range(m):
        theta_path_sgd.append(theta)
        if epoch == 0 and i < 10:
            y_line_predict = X_line_b @ theta
            linestyle = 'r--' if i == 0 else 'b-'
            label = '初始状态' if i == 0 else None
            plt.plot(X_line, y_line_predict, linestyle, label=label)
        random_index = np.random.randint(m)
        xi = X_b[random_index:random_index+1]
        yi = y[random_index:random_index+1]
        gradients = 2 * xi.T @ (xi @ theta - yi)
        eta = learning_schedule(epoch * m + i)
        theta = theta - eta * gradients
print("参数:", theta.reshape(-1))  # [2.19377016 3.87214289]

plt.plot(X, y, "b.")
plt.xlabel("$x_1$")
plt.ylabel("$y$", rotation=0)
plt.axis([0, 2, 0, 12])
plt.legend()
save_fig("sgd")
plt.show()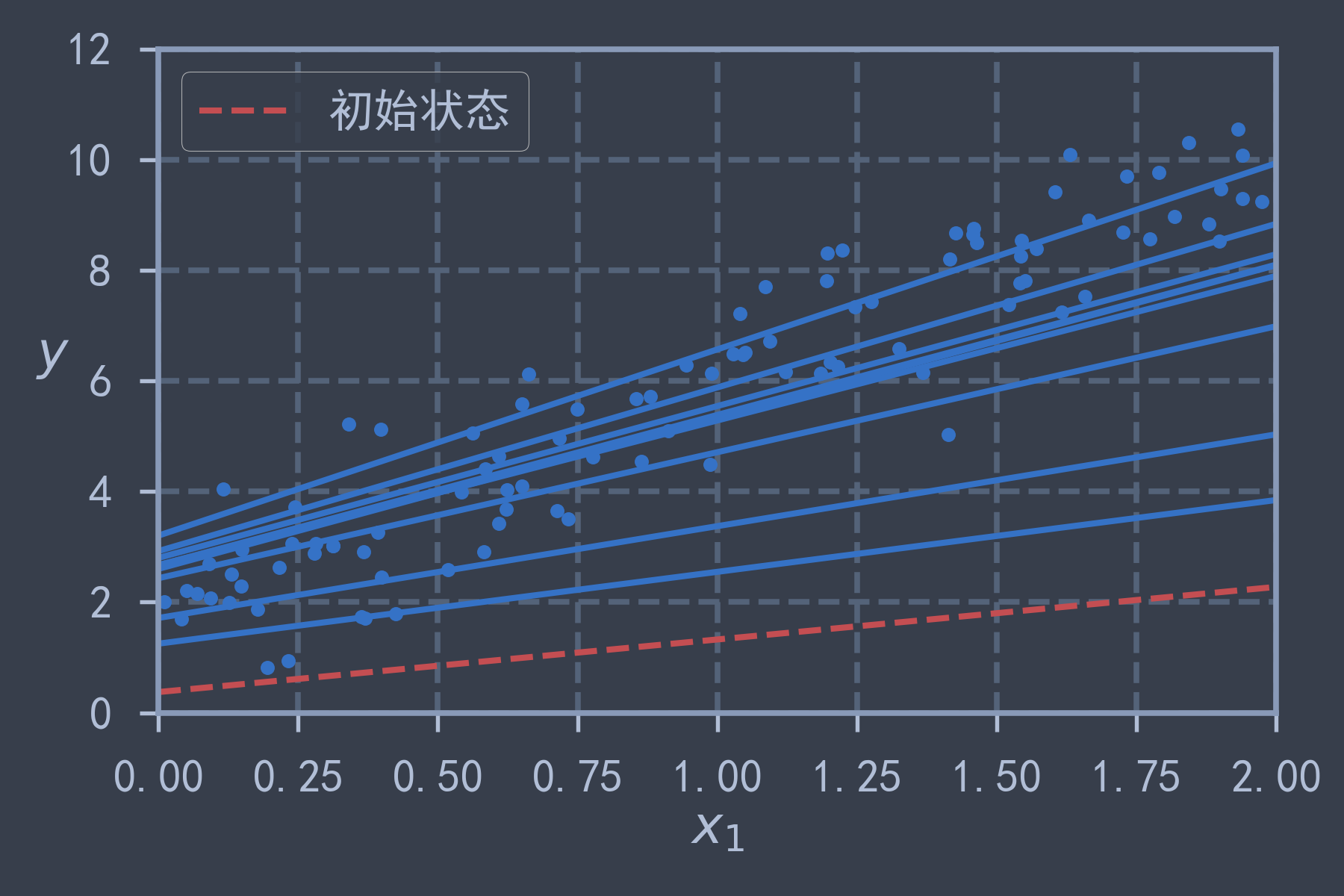

from sklearn.linear_model import SGDRegressor

sgd_reg = SGDRegressor(max_iter=1000, penalty=None, eta0=0.1, random_state=42)
sgd_reg.fit(X, y)
print(sgd_reg.intercept_, sgd_reg.coef_)  # [2.26548882] [3.80567955]

小批量梯度下降(Mini-batch gradient descent, Mini-BGD)

theta_path_mbgd = []
n_epoch = 200
batch_size = 20
np.random.seed(42)
theta = np.random.rand(2, 1)
t0, t1 = 200, 1000
def learning_schedule(t):
    return t0 / (t1 + t)

for epoch in range(n_epoch):
    shuffled_indices = np.random.permutation(m)
    X_b_shuffled = X_b[shuffled_indices]
    y_shuffled = y[shuffled_indices]
    for i in range(0, m, batch_size):
        theta_path_mbgd.append(theta)
        xi = X_b[i:i+batch_size+1]
        yi = y[i:i+batch_size+1]
        gradients = 2/batch_size * xi.T @ (xi @ theta - yi)
        eta = learning_schedule(epoch * (m // batch_size) + i)
        theta = theta - eta * gradients
print("参数:", theta.reshape(-1))  # [2.21497588 3.89786208]

theta_path_bgd = np.array(theta_path_bgd)
theta_path_sgd = np.array(theta_path_sgd)
theta_path_mbgd = np.array(theta_path_mbgd)

plt.figure(figsize=(8, 5))
plt.plot(theta_path_sgd[:, 0], theta_path_bgd[:, 1], 'r-s', markersize='6', lw=1, label="SGD")
plt.plot(theta_path_mbgd[:, 0], theta_path_bgd[:, 1], 'g-*', lw=2, label="Mini-BGD")
plt.plot(theta_path_bgd[:, 0], theta_path_bgd[:, 1], 'b-o', markersize='8',lw=3, label="BGD")
# plt.axis([1.5, 3.2, 2.4, 3.9])
plt.legend()
plt.xlabel(r"$\theta_0$")
plt.ylabel(r"$\theta_1$", rotation=0)
save_fig("gradient_descent_paths")
plt.show()  # 从下图可以看出BGD的方差是最小的最稳定，而SGD最不稳定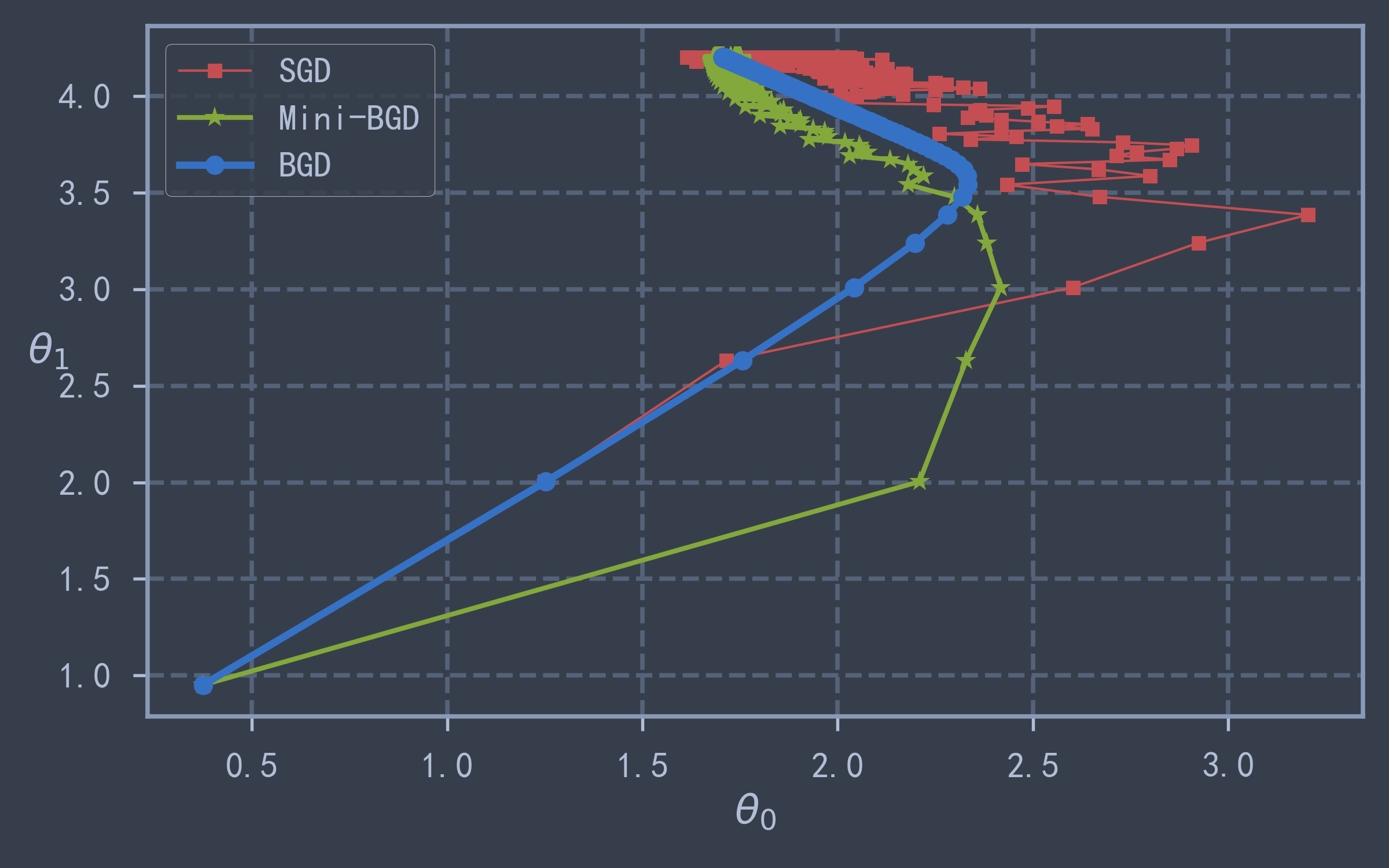

2.多项式回归

m = 100
np.random.seed(42)
X = 4 * np.random.rand(m, 1) - 2
np.random.seed(42)
y = 8 + 2* X - X**2 + np.random.randn(m, 1)

plt.plot(X, y, 'b.')
plt.xlabel("$x_1$")
plt.ylabel("$y$", rotation=0)
plt.axis([-2, 2, 0, 11])
save_fig("generated_quadratic_data")
plt.show()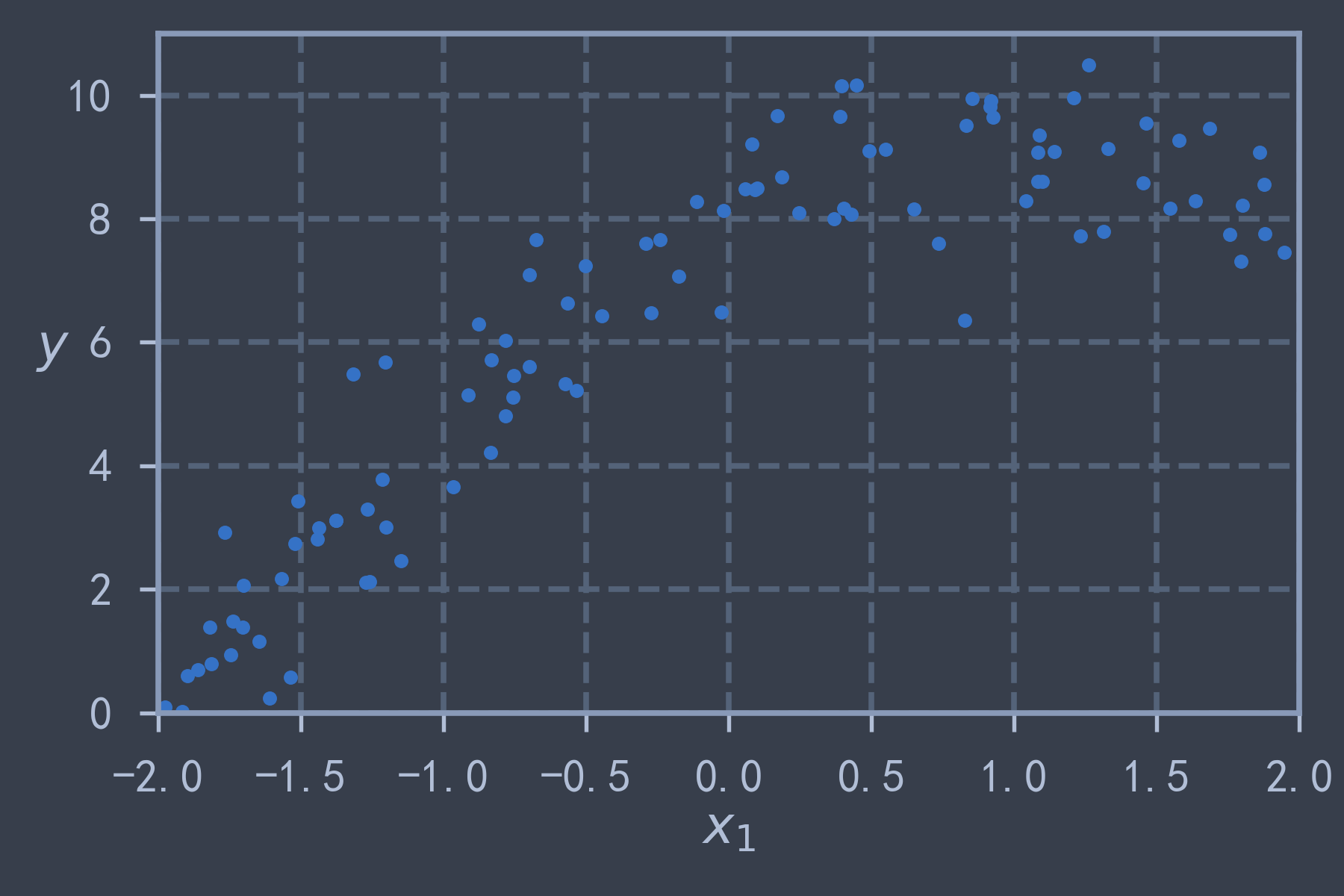

使用 sklearn.preprocessing.PolynomialFeatures(degree, include_bias=False) 可以生成最大幂次为 degree 的全部特征组合，include_bias=False 表示不包含偏置项，在线性回归的时候默认带了偏置，此处就无须该项.

from sklearn.preprocessing import PolynomialFeatures
poly_features = PolynomialFeatures(degree=2, include_bias=False)
X_poly = poly_features.fit_transform(X)
print(f"{X[0]} -> {X_poly[0]}")  # [-0.50183952] -> [-0.50183952  0.25184291]
lin_reg = LinearRegression()
lin_reg.fit(X_poly, y)
print(lin_reg.intercept_, lin_reg.coef_)  # [7.96332948] [[ 2.09663123 -1.03929909]] 与真实值 8 2 -1 相差很小

X_new = np.linspace(-2, 2, 100).reshape(100, 1)  # 在[-2,2]上等距取100个点
X_new_poly = poly_features.transform(X_new)
y_new = lin_reg.predict(X_new_poly)
plt.plot(X, y, 'b.')
plt.plot(X_new, y_new, 'r-', lw=2, label="预测值")
plt.xlabel("$x_1$")
plt.ylabel("$y$", rotation=0)
plt.axis([-2, 2, 0, 11])
plt.legend()
save_fig("quadratic_predictions")
plt.show()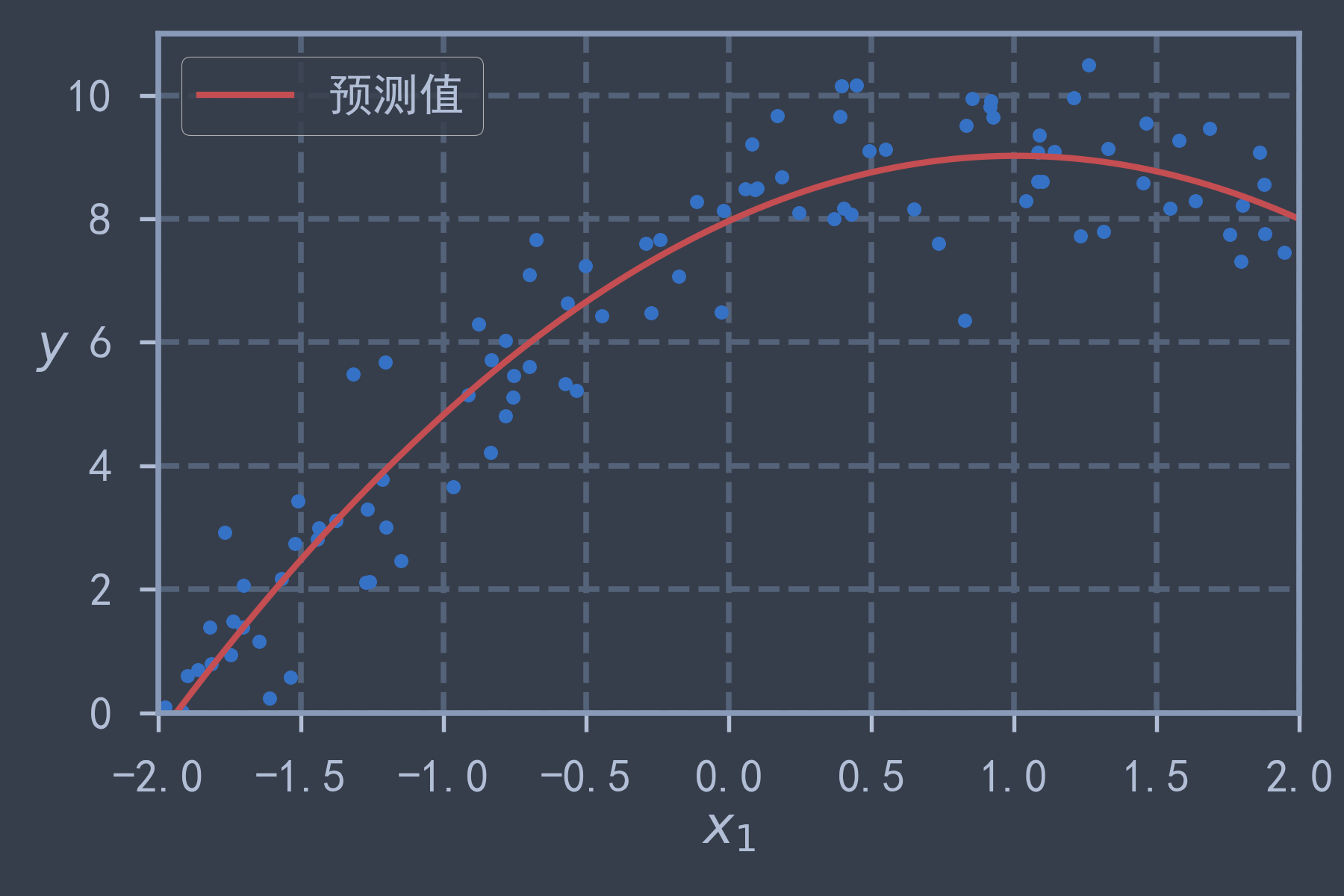

使用 sklearn.preprocessing.StandardScaler 进行标准化处理，sklearn.pipeline.Pipeline 生成数据预处理和模型训练的流水线.

from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline

for style, linewidth, degree in (('g-', 1, 300), ('b--', 2, 2), ('r-', 2, 1)):
    polynomial_pipeline = Pipeline([
        ("poly_features", PolynomialFeatures(degree=degree, include_bias=False)),
        ("std_scaler", StandardScaler()),
        ("lin_reg", LinearRegression())
    ])
    polynomial_pipeline.fit(X, y)
    y_new = polynomial_pipeline.predict(X_new)
    plt.plot(X_new, y_new, style, lw=linewidth, label=str(degree))
    
plt.plot(X, y, 'b.')
plt.legend(loc="upper left")
plt.xlabel("$x_1$")
plt.ylabel("$y$", rotation=0)
plt.axis([-2, 2, 0, 11])
save_fig("high_degree_polynoimals")
plt.show()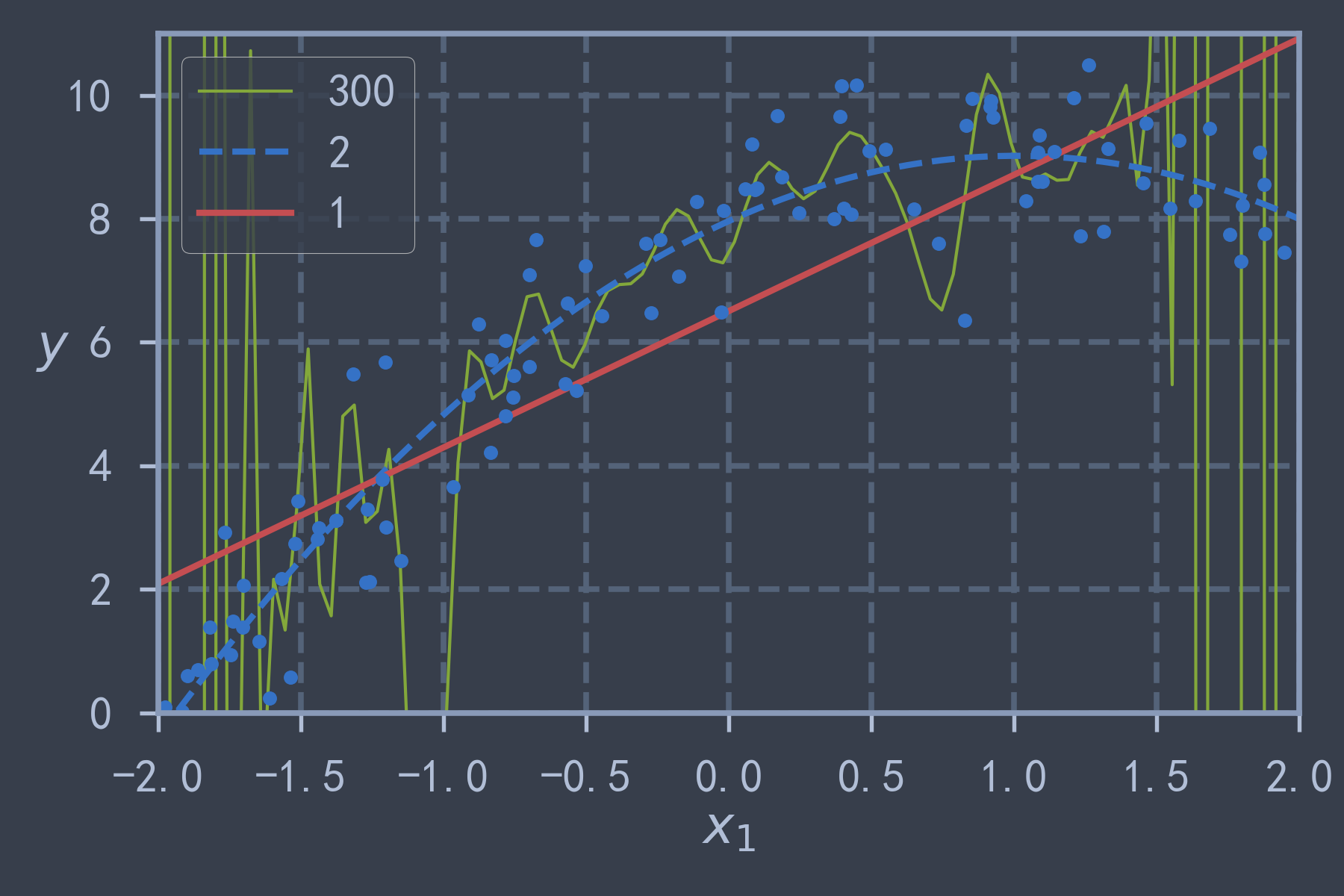

正则化线性模型

岭回归

使用 sklearn.linear_model.Ridge(alpha) 可以实现岭回归，使用 $l_2$ 正则项，其中 alpha 是正则化系数.

m = 20
np.random.seed(42)
X = 3 * np.random.rand(m, 1)
np.random.seed(42)
y = 1 + 0.5 * X + np.random.randn(m, 1) / 1.5
X_new = np.linspace(0, 3, 100).reshape(100, 1)

from sklearn.linear_model import Ridge

def plot_model_curve(model_class, polynomial, alphas, **model_kargs):
    for alpha, style in zip(alphas, ('b-', 'g--', 'r:')):
        model = model_class(alpha, **model_kargs) if alpha > 0 else LinearRegression()
        if polynomial:
            model = Pipeline([
                ("poly_features", PolynomialFeatures(degree=10, include_bias=False)),
                ("std_scaler", StandardScaler()),
                ("regular_reg", model)
            ])
        model.fit(X, y)
        y_new = model.predict(X_new)
        linewidth = 2 if alpha == 0 else 3
        plt.plot(X_new, y_new, style, lw=linewidth, label=f"$\\alpha={alpha}$")
    plt.plot(X, y, 'b.')
    plt.legend(loc="lower right")
    plt.xlabel("$x_1$")
    plt.axis([0, 3, 0, 3])
plt.figure(figsize=(10, 4))
plt.subplot(121)
plot_model_curve(Ridge, polynomial=False, alphas=(0, 10, 100), random_state=42)
plt.ylabel("$y$", rotation=0)
plt.subplot(122)
plot_model_curve(Ridge, polynomial=True, alphas=(0, 1e-5, 1), random_state=42)
save_fig("ridge_regression")
plt.show()  # 从下图中可以看出，正则项越大，曲线斜率越小，更加平缓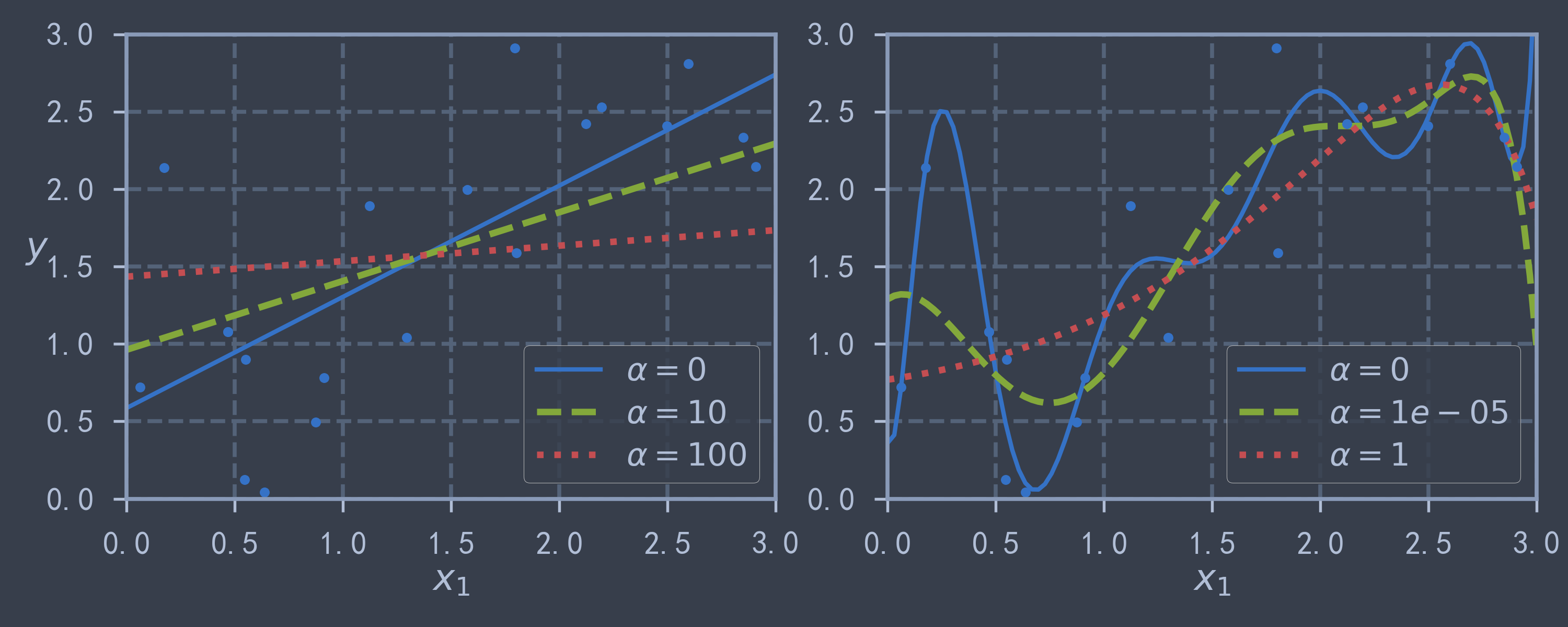

Lasso回归

使用 sklearn.linear_model.Lasso 实现Lasso回归，使用 $l_1$ 正则项，用法与 Ridge 类似.

from sklearn.linear_model import Lasso

plt.figure(figsize=(10, 4))
plt.subplot(121)
plot_model_curve(Lasso, polynomial=False, alphas=(0, 0.3, 1), random_state=42)
plt.ylabel("$y$", rotation=0)
plt.subplot(122)
plot_model_curve(Lasso, polynomial=True, alphas=(0, 1e-5, 1), random_state=42)
save_fig("lasso_regression")
plt.show()  # 与岭回归进行对比，可以发现相同的正则系数下，Lasso回归的曲线更加平缓，对参数抑制更强
# 而且alpha不能太大，否则模型参数全部抑制为0了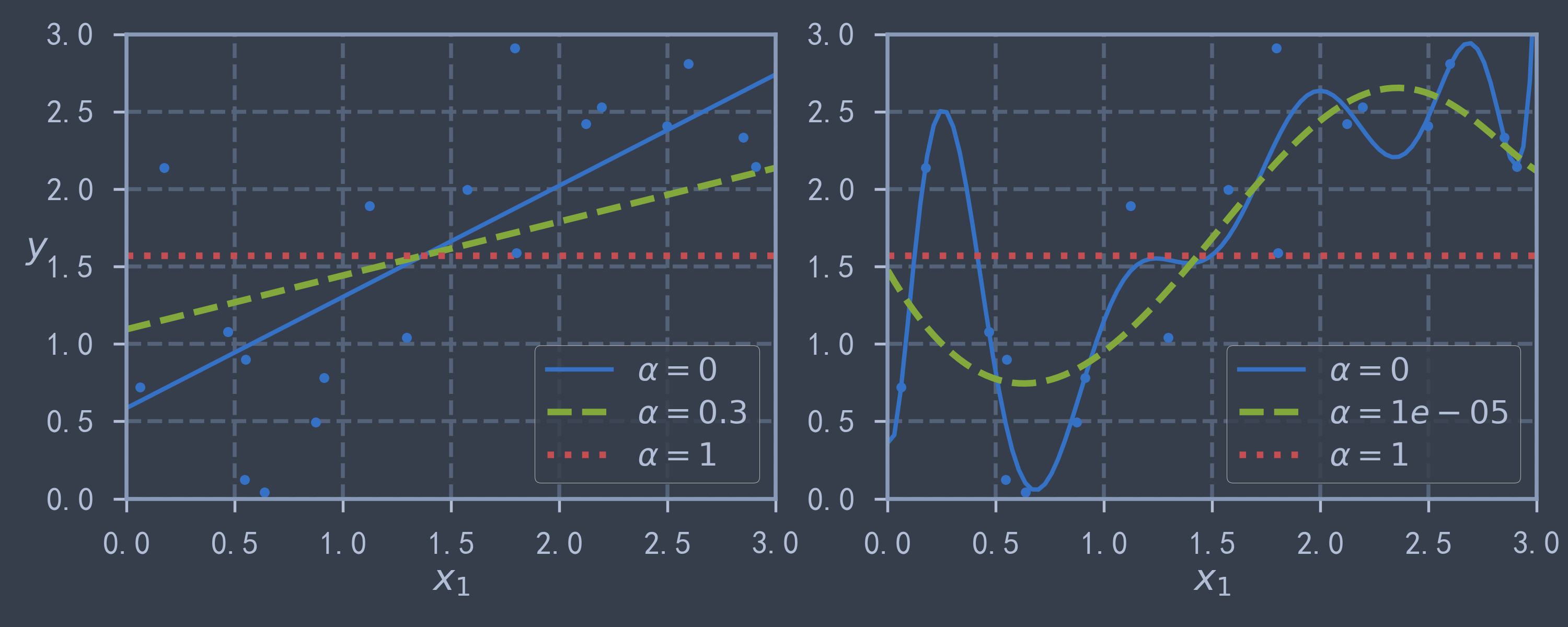

弹性网络

使用 sklearn.linear_model.ElasticNet(l1_ratio) 实现弹性网络，其中 l1_ratio 表示 $l_1$ 范数所占的权重，正则化项的具体表示形式如下：

$$\alpha \left(l_{1_{ratio}} ||w||_1 + \frac{1}{2} (1 - l_{1_{ratio}})||w||^2_2\right)$$

from sklearn.linear_model import ElasticNet

plt.figure(figsize=(10, 4))
plt.subplot(121)
plot_model_curve(ElasticNet, polynomial=False, alphas=(0, 0.3, 1), l1_ratio=0.2, random_state=42)
plt.ylabel("$y$", rotation=0)
plt.subplot(122)
plot_model_curve(ElasticNet, polynomial=True, alphas=(0, 1e-5, 1), l1_ratio=0.2, random_state=42)
save_fig("elasticnet_regression")
plt.show()  # 而弹性网络则是对上述两者的综合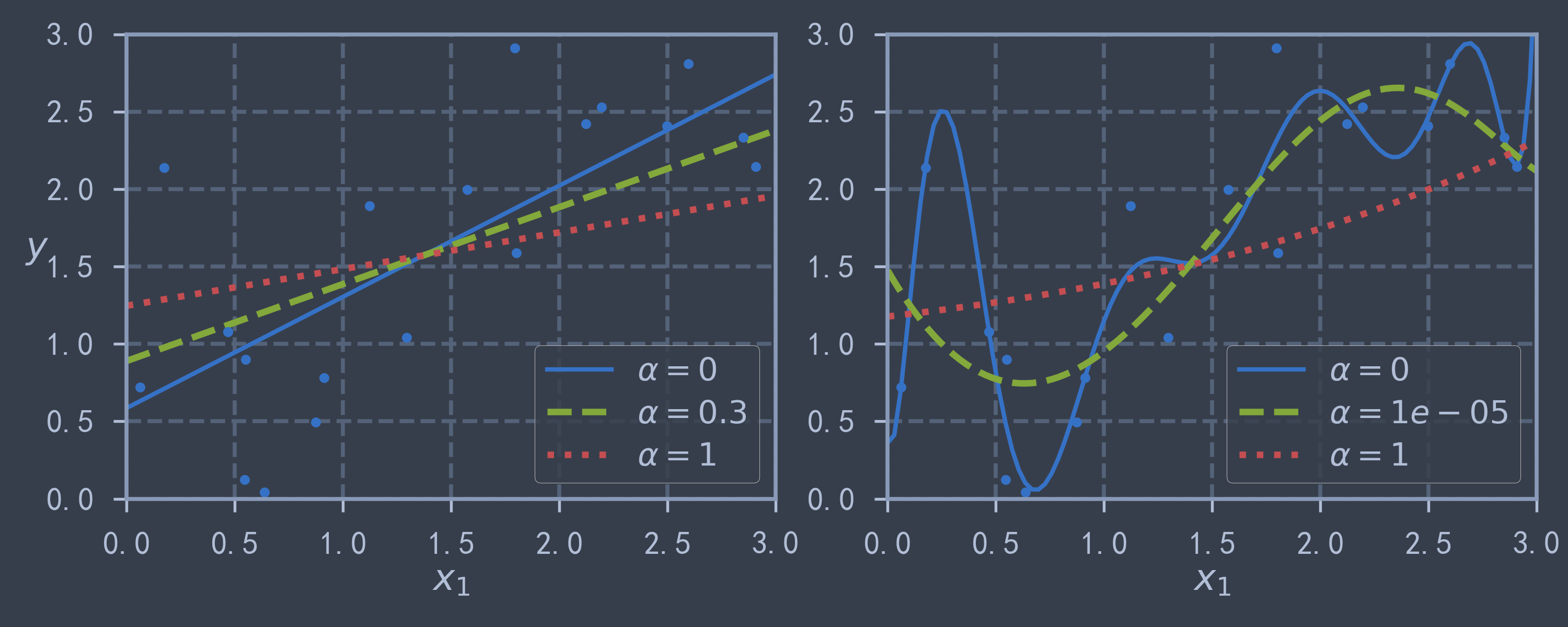

theta1_a, theta1_b, theta2_a, theta2_b = -1, 3, -1.5, 1.5  # 设定参数的取值范围
theta1_linspace = np.linspace(theta1_a, theta1_b, 500)  # 获取theta1的均匀插值点
theta2_linspace = np.linspace(theta2_a, theta2_b, 500)  # 获取theta2的均匀插值点
theta1, theta2 = np.meshgrid(theta1_linspace, theta2_linspace)  # 网格化对应(theta1, theta2)，得到参数向量
Theta = np.c_[theta1.ravel(), theta2.ravel()]  # 构造参数矩阵Theta

X = np.array([[1, -1], [1, 0.5], [1, 1]])  # 构造训练样本特征
y = 2 * X[:, :1] + 1 * X[:, 1:]  # 以函数y=2+x生成对应标签
m = len(X)  # 训练集大小

# 求解每个(theta1,theta2)对应的不带正则项的成本函数值
J = (1/m * np.sum((X @ Theta.T - y) ** 2, axis=0)).reshape(theta1.shape)

N1 = np.linalg.norm(Theta, ord=1, axis=1).reshape(theta1.shape)  # 求解每个(theta1,theta2)对应的l1范数
N2 = np.linalg.norm(Theta, ord=2, axis=1).reshape(theta1.shape)  # 求解每个(theta1,theta2)对应的l2范数

theta_min_index = np.unravel_index(np.argmin(J), J.shape)  # 求最小值对应的下标
theta1_min, theta2_min = theta1[theta_min_index], theta2[theta_min_index]  # 最优参数[1.998, 0.502]
theta_init = np.array([[0], [-1]])  # 初始参数向量

# 使用批量梯度下降BGD，并用list返回参数变化，l1，l2分别表示l1和l2正则化系数，core=0表示最小化参数范数(原点处最小)
def bgd_path(theta, X, y, l1, l2, core=1, eta=0.05, n_iterations=200):
    theta_path = [theta]  # 先存储theta初始值
    for i in range(n_iterations):
        gradients = core * 2/m * X.T @ (X @ theta - y) + l1 * np.sign(theta) + l2 * theta
        theta = theta - eta * gradients
        theta_path.append(theta)
    return np.array(theta_path)

fig, axes = plt.subplots(2, 2, sharex=True, sharey=True, figsize=(10, 8))  # 构造2x2的画板，共享x,y轴
for i, N, l1, l2, title in ((0, N1, 2, 0, "Lasso"), (1, N2, 0, 2, "Ridge")):  # 按行绘制图像，分别绘制l1范数和l2范数对应轨迹
    JR = J + l1 * N1 + l2 * 0.5 * N2**2  # 计算带有正则项的成本函数
    
    theta_regular_index = np.unravel_index(np.argmin(JR), JR.shape)  # 求出在正则化之后最小值对应下标
    theta1_regular_min, theta2_regular_min = theta1[theta_regular_index], theta2[theta_regular_index]
    
    levelsJ = (np.exp(np.linspace(0, 1, 20)) - 1) * (np.max(J) - np.min(J)) + np.min(J) # 构造J的等高线，使用指数分布采样
    levelsJR = (np.exp(np.linspace(0, 1, 20)) - 1) * (np.max(JR) - np.min(JR)) + np.min(JR) # 构造JR的等高线，使用指数分布采样
    levelsN = np.linspace(0, np.max(N), 10)  # 构造参数范数的等高线，均匀采样

    path_J = bgd_path(theta_init, X, y, l1=0, l2=0)  # 不使用正则化项
    path_JR = bgd_path(theta_init, X, y, l1, l2)  # 使用对应正则化项
    path_N = bgd_path(np.array([[2], [1]]), X, y, l1/6, l2, core=0)  # 从(2,0.5)开始，最小化范数
    
    ax = axes[i, 0]
    ax.axhline(y=0, color='k')  # 绘制y轴
    ax.axvline(x=0, color='k')  # 绘制x轴
    ax.contourf(theta1, theta2, N/2., levels=levelsN)
    ax.plot(path_N[:, 0], path_N[:, 1], 'y--')
    ax.plot(0, 0, 'rs', label='最优点')
    ax.plot([2], [1], "gs", label='起始点')
    ax.set_title(f"$\\ell_{i+1}$")
    ax.axis([theta1_a, theta1_b, theta2_a, theta2_b])
    if i == 1:
        ax.set_xlabel(r"$\theta_1$")
    ax.set_ylabel(r"$\theta_2$", rotation=0)
    ax.legend()
    
    ax = axes[i, 1]
    ax.axhline(y=0, color='k')  # 绘制y轴
    ax.axvline(x=0, color='k')  # 绘制x轴
    ax.contourf(theta1, theta2, JR, levels=levelsJR, alpha=0.8)
    ax.plot(path_JR[:, 0], path_JR[:, 1], 'y-o')
    ax.plot(theta1_regular_min, theta2_regular_min, 'ro', label=f'$\\ell_{i+1}$最优点')
    ax.plot(theta_init[0], theta_init[1], "go", label='起始点')
    ax.set_title(title)
    ax.axis([theta1_a, theta1_b, theta2_a, theta2_b])
    if i == 1:
        ax.set_xlabel(r"$\theta_1$")
    ax.plot(theta1_min, theta2_min, 'bo', label='原问题最优点')
    ax.legend()
save_fig("lasso_vs_ridge")
plt.show()  # 从下图中可以看出Lasso回归中theta2几乎为0
# 由于原始最优解theta2<theta1，所以x1相对x0权重较低，Lasso回归中直接将其置为0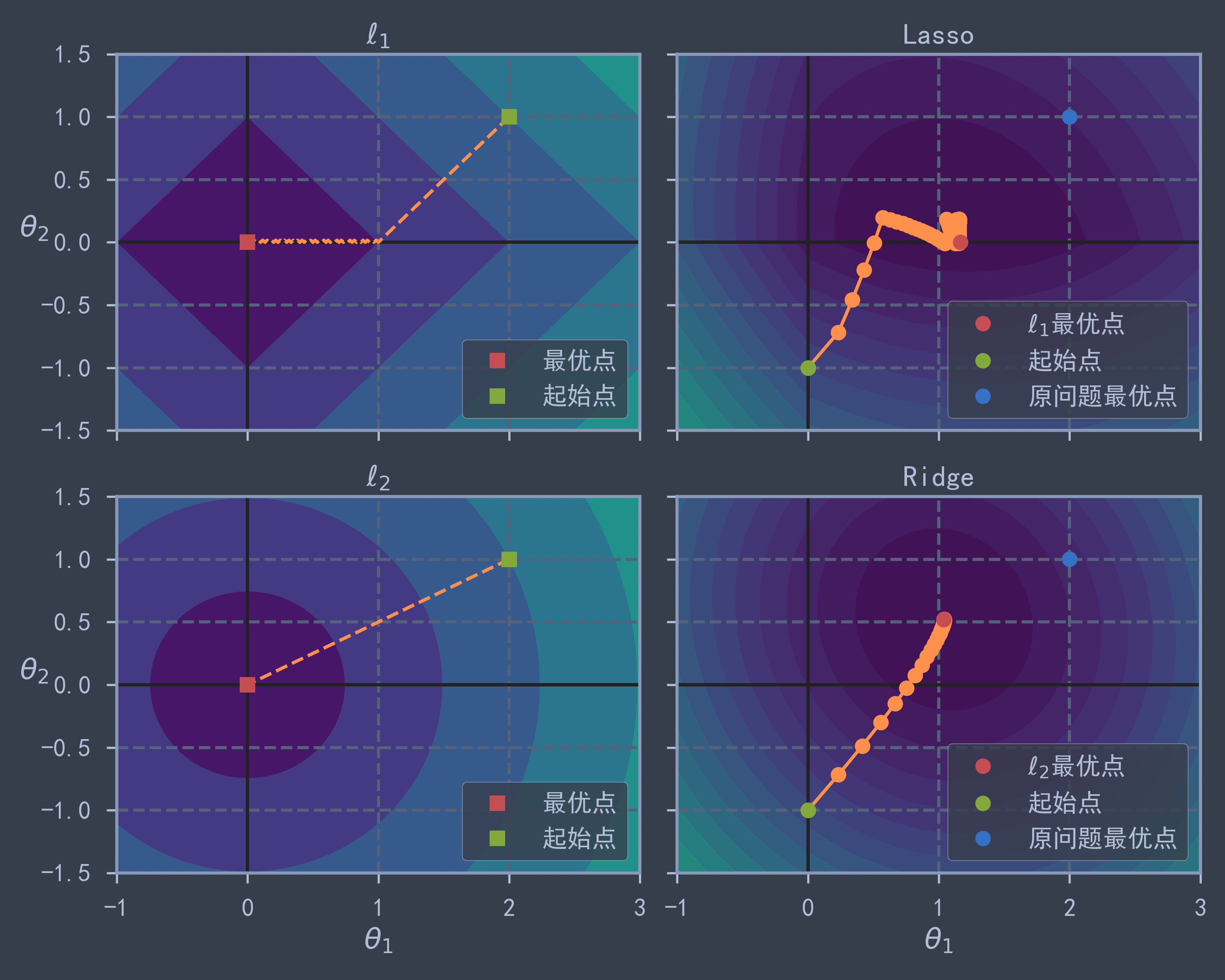

plt.axhline(y=0, color='k')  # 绘制y轴
plt.axvline(x=0, color='k')  # 绘制x轴
plt.contourf(theta1, theta2, J, levels=levelsJ, alpha=0.8)
plt.plot(path_J[:, 0], path_J[:, 1], 'y-o')
plt.plot(theta1_min, theta2_min, 'bo', label='原问题最优点')
plt.plot(theta_init[0], theta_init[1], "go", label='起始点')
plt.title("BGD无正则化")
plt.axis([theta1_a, theta1_b, theta2_a, theta2_b])
plt.xlabel(r"$\theta_1$")
plt.ylabel(r"$\theta_2$", rotation=0)
plt.legend()
save_fig("BGD_without_regular")
plt.show()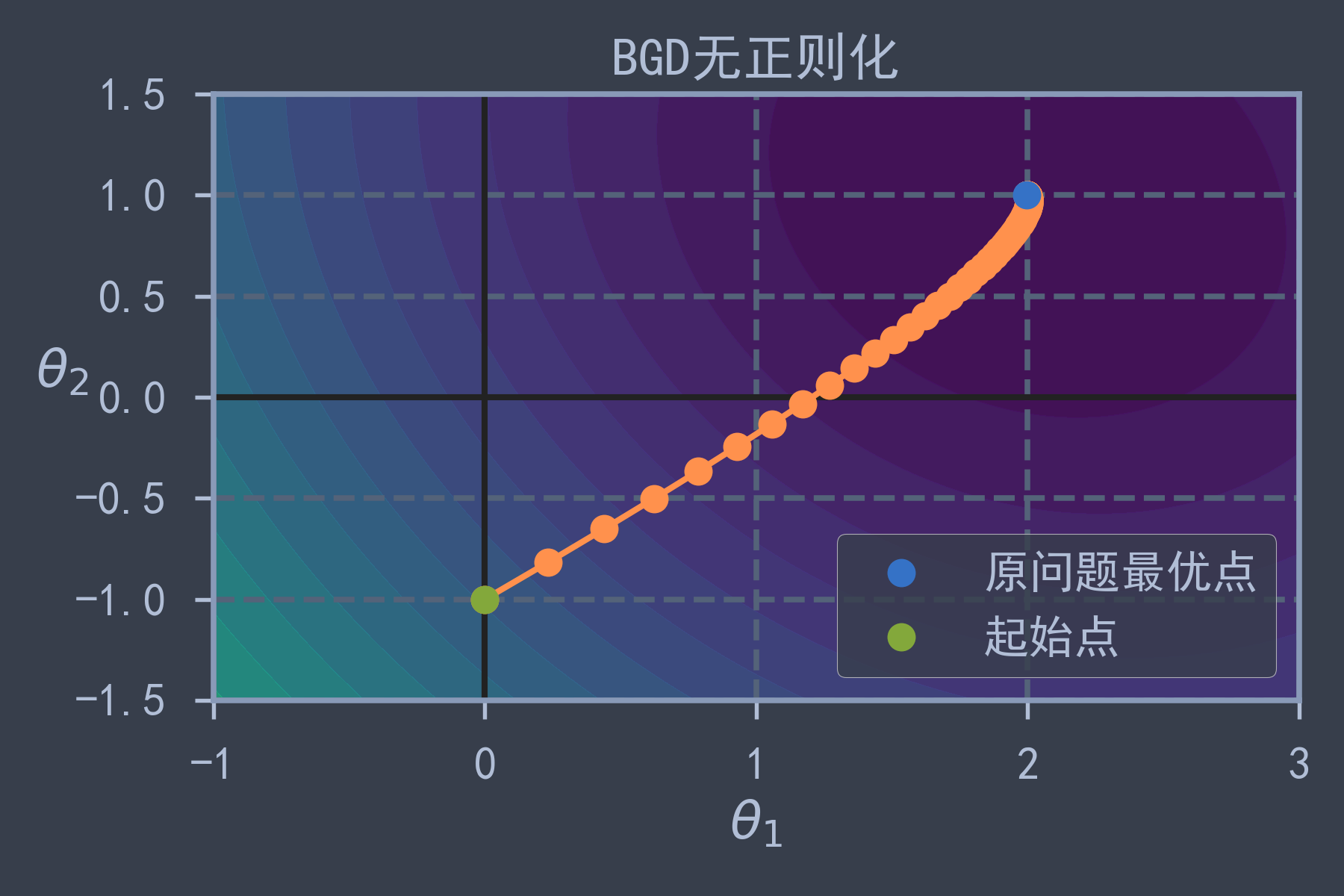

3.Logistic回归

使用经典Iris数据集，包含150个鸢尾花，来自三个不同品种（山鸢尾，变色鸢尾，弗吉尼亚鸢尾），数据特征属性总共4个，分别为包含萼片的长度与宽度，花瓣的长度和宽度.

先使用花边宽度单个属性值对品种是否是弗吉尼亚鸢尾花进行预测，再使用花瓣宽度和长度两个属性值进行预测，分别绘制出决策边界和样本点图像.

使用 sklearn.linear_model.LogisticRegression(C) 实现Logistic回归，默认使用 $l_2$ 正则化项，正则化系数为 $1/C$，如果不想使用正则化，可将 $C$ 设置为较大值.

from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression

iris = load_iris()
print(iris.DESCR)  # 查看该数据集的相关信息
print(iris.keys())  # 通过关键词索引可以获取数据集中的信息
X = iris['data'][:, 3:]  # 花瓣宽度
y = (iris['target']==2).astype(np.int)  # 弗吉尼亚鸢尾
log_reg = LogisticRegression(random_state=42)
log_reg.fit(X, y)

X_new = np.linspace(0, 3, 1000).reshape(-1, 1)
y_new_proba = log_reg.predict_proba(X_new)
decision_boundary = X_new[y_new_proba[:, 1] >= 0.5][0]  # 决策边界

plt.figure(figsize=(9, 4))
plt.plot(X[y==1], y[y==1], 'g^', label='弗吉尼亚鸢尾')
plt.plot([decision_boundary, decision_boundary], [-1, 2], 'w:', lw=2)
plt.plot(X_new, y_new_proba[:, 1], 'g-', label='弗吉尼亚鸢尾')
plt.plot(X[y==0], y[y==0], 'bs', label='非弗吉尼亚鸢尾')
plt.plot(X_new, y_new_proba[:, 0], 'b--', label='非弗吉尼亚鸢尾')
plt.text(decision_boundary, 0.15, '决策边界', fontsize=16, ha='center')
plt.arrow(decision_boundary, 0.1, -0.3, 0, head_width=0.05, head_length=0.08, width=0.01, fc='b', ec='b')
plt.arrow(decision_boundary, 0.9, 0.3, 0, head_width=0.05, head_length=0.08, width=0.01, fc='g', ec='g')
plt.xlabel("花瓣宽度(cm)")
plt.ylabel("概率")
plt.axis([0, 3, -0.03, 1.03])
plt.legend(loc='center left')
save_fig('logistic_regression')
plt.show()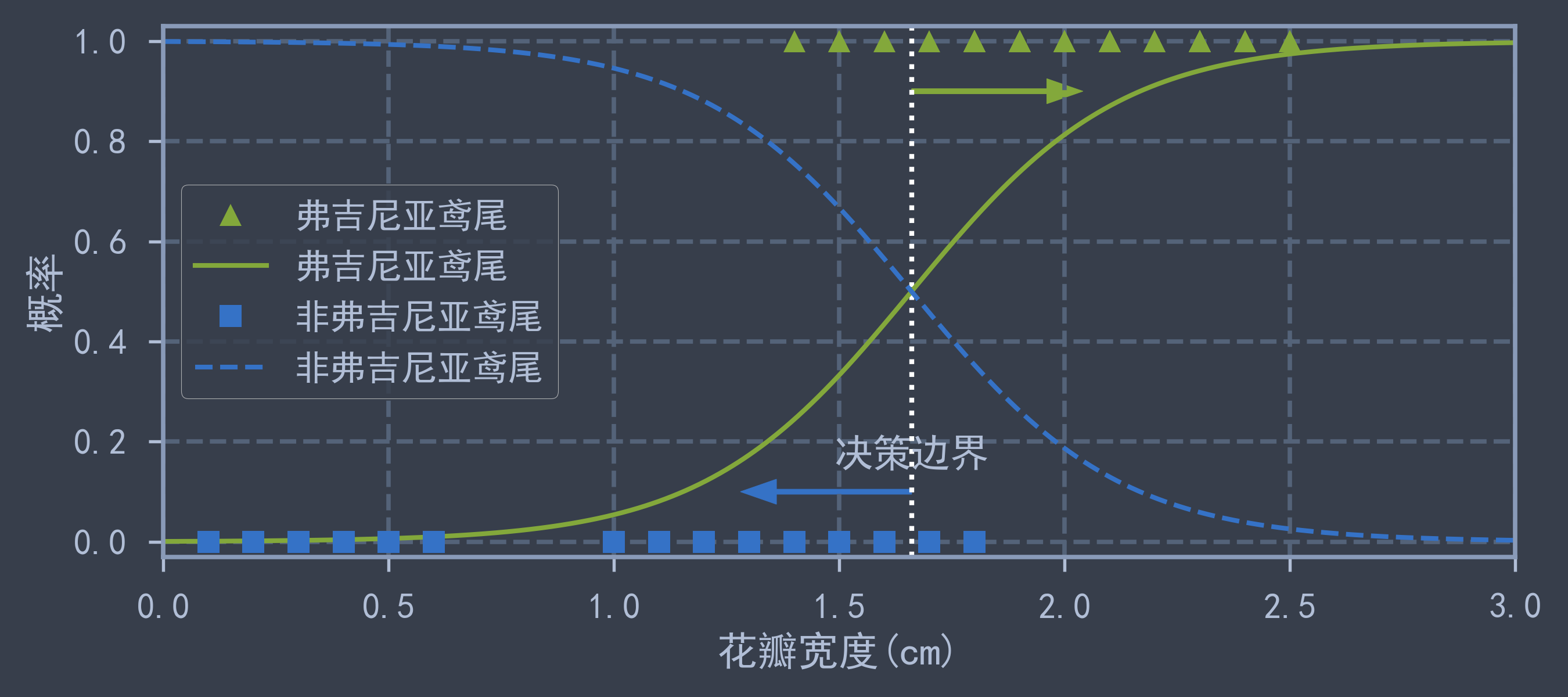

X = iris['data'][:, (2,3)]  # 获取花瓣的长度和宽度
y = (iris['target'] == 2).astype(np.int)  # 判断是否为弗吉尼亚鸢尾

log_reg = LogisticRegression(C=1e10, random_state=42)  # 不使用正则化
log_reg.fit(X, y)

x0, x1 = np.meshgrid(  # 网格化
    np.linspace(2.9, 7, 500),
    np.linspace(0.8, 2.7, 200)
)
X_new = np.c_[x0.ravel(), x1.ravel()]  # 网格化数据集
y_new_proba = log_reg.predict_proba(X_new)  # 计算网格点概率

plt.figure(figsize=(10, 4))
plt.plot(X[y==1, 0], X[y==1, 1], 'g^', label='弗吉尼亚鸢尾')
plt.plot(X[y==0, 0], X[y==0, 1], 'bs', label='非弗吉尼亚鸢尾')
z = y_new_proba[:, 1].reshape(x0.shape)  # 每个网格点预测为真的概率
contour = plt.contour(x0, x1, z, cmap='autumn')  # 绘制等高线(等概率线)
plt.clabel(contour, inline=1)  # 在等高线上写对应概率
plt.axis([2.9, 7, 0.8, 2.7])
plt.xlabel("花瓣长度(cm)")
plt.ylabel("花瓣宽度(cm)")
plt.legend(loc='center left')
save_fig("logistic_regression_contour")
plt.show()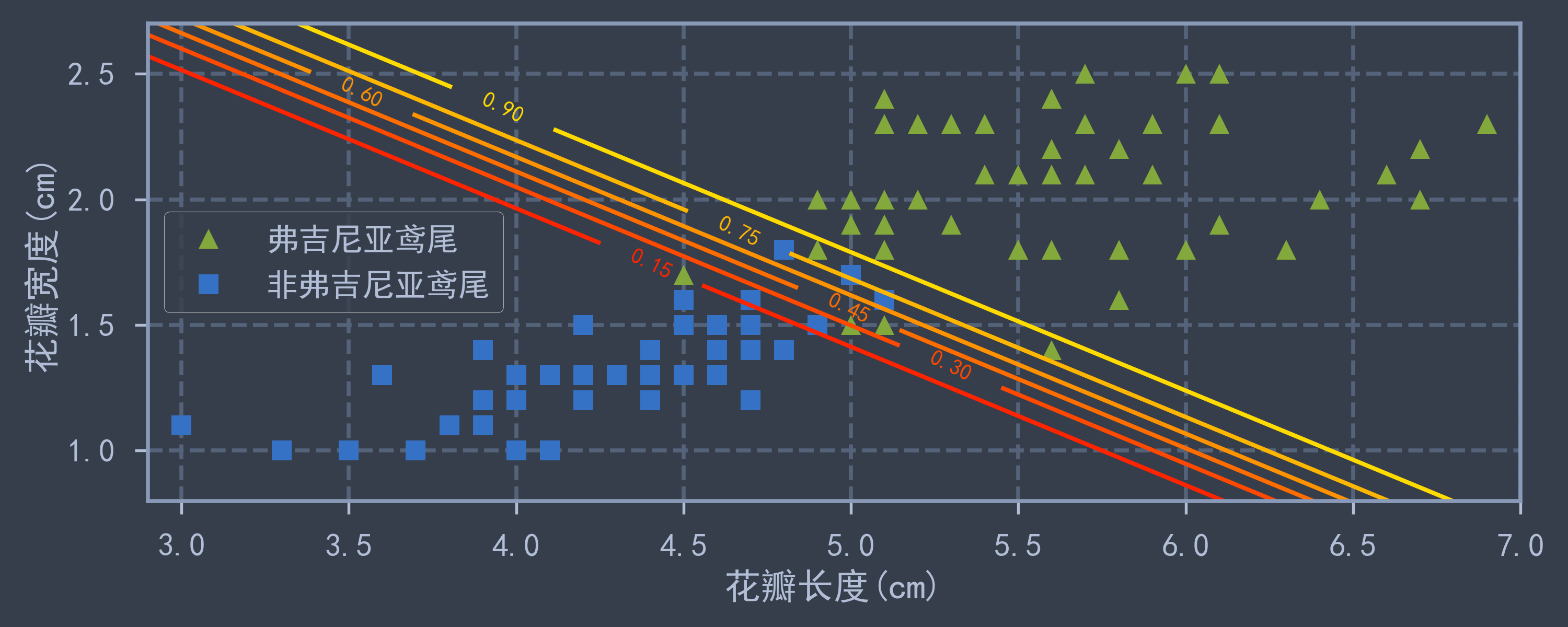

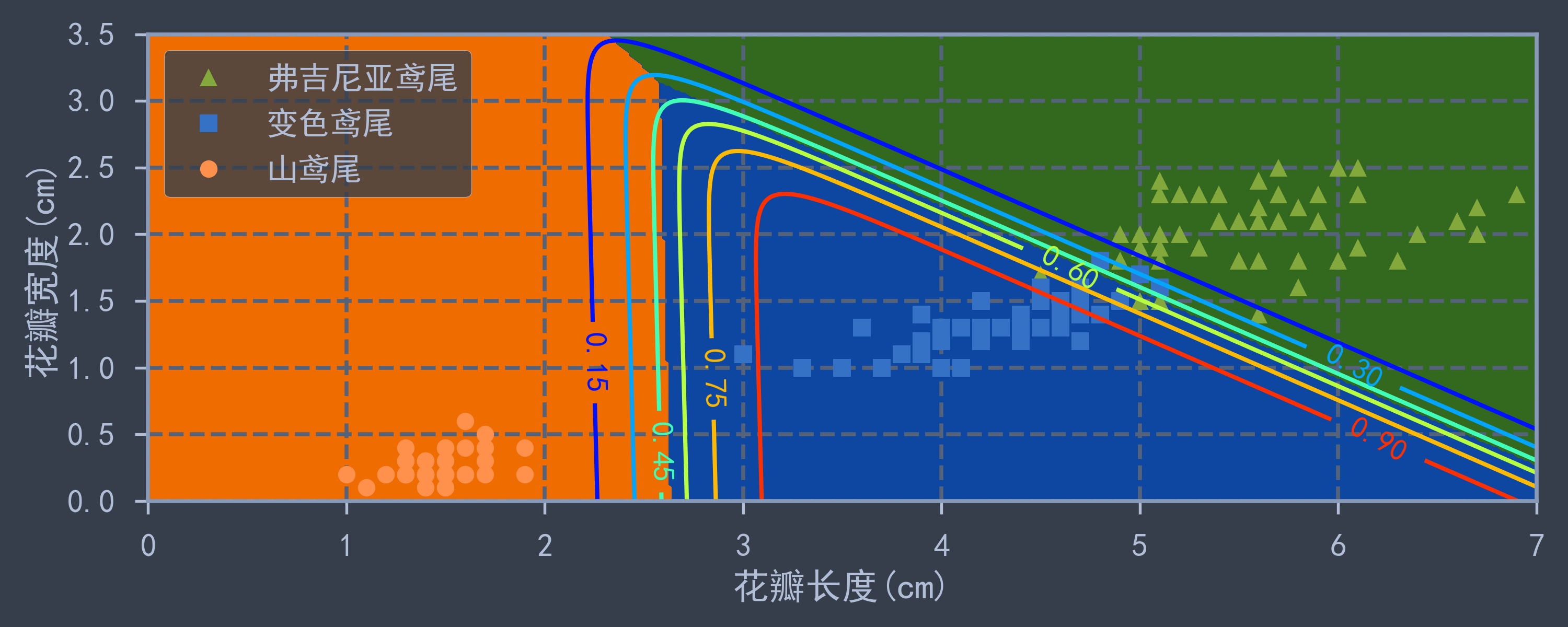
4.Softmax回归

也是使用 sklearn.linear_model.LogisticRegression(multi_class='multinomial')，只需将 multi_class 设置为 multinomial 即可使用Softmax回归求解多分类任务（否则可能使用“一对多(OvR)”分类策略）

特征属性仍然选取两个属性：花瓣长度，花瓣宽度. 分类目标为三种鸢尾花，绘制预测为“变色鸢尾”的等概率边界线.

X = iris['data'][:, (2,3)]  # 获取花瓣的长度和宽度
y = iris['target']

log_reg = LogisticRegression(multi_class='multinomial', C=10, random_state=42)
log_reg.fit(X, y)

x0, x1 = np.meshgrid(  # 网格化
    np.linspace(0, 8, 500),
    np.linspace(0, 3.5, 200)
)
X_new = np.c_[x0.ravel(), x1.ravel()]  # 网格化数据集
y_new_prob = log_reg.predict_proba(X_new)  # 计算网格点概率
y_new_pred = log_reg.predict(X_new)  # 计算网格点预测结果

plt.figure(figsize=(10, 4))
plt.plot(X[y==2, 0], X[y==2, 1], 'g^', markersize=8, label='弗吉尼亚鸢尾')
plt.plot(X[y==1, 0], X[y==1, 1], 'bs', markersize=8, label='变色鸢尾')
plt.plot(X[y==0, 0], X[y==0, 1], 'yo', markersize=8, label='山鸢尾')
z_prob = y_new_prob[:, 1].reshape(x0.shape)  # 获取预测为"变色鸢尾"的概率
z_cate = y_new_pred.reshape(x0.shape)  # 用于绘制区块颜色

custom_cmap = mpl.colors.ListedColormap(['#EF6C00', '#0D47A1', '#33691E'])  # 自定义cmap颜色谱
plt.contourf(x0, x1, z_cate, cmap=custom_cmap)

contour = plt.contour(x0, x1, z_prob, cmap='jet')
plt.clabel(contour, inline=1, fontsize=14)
plt.xlabel('花瓣长度(cm)')
plt.ylabel('花瓣宽度(cm)')
plt.legend()
plt.axis([0, 7, 0, 3.5])
save_fig("softmax_regression_contour")
plt.show()