遗传算法的基本原理及代码

遗传算法是一种模拟自然界物种进化的算法，通过模拟一个种群的基因在自然环境下，遵循“优胜劣汰，适者生存”的达尔文进化理论，基因不断的迭代，从而进化。

理想是这个样的，此算法用于求解最优化问题，效果应该还行，下文讲解了算法的思路和具体实现方法。

变量声明

WLOG将问题转化为：多变量最大化目标函数值。

英文名字都是我自己取得，很可能不严谨~

基因（组）：（Gene & Genome）由一个（或多个）二进制串构成，二进制串的每一位代表基因所携带的信息，基因的个数可以根据题目中自变量的个数确定，记为 $x_i$

P.S. 在实际问题中，可能有多个自变量控制一个因变量，同时可能有多个限制条件，这里将每个自变量与一个基因建立同构关系，假设实际问题中存在 $n$ 个自变量，则以下变量都可视为 $n$ 维向量

基因长度：（Length of Gene）每一个二进制串的位数，记为 $L$

种群：（Population）由基因所组成的可重集合，记为 $P$

种群大小：（Number of Gene）记为 $N = |P|$

基因空间：（Gene Space）由所有基因所组成的空间，记为 $S$ ，不难发现如果基因维数为 $1$ 且 $S$ 由所有位数为 $L$ 的二进制串构成，则 $S = \{0, 1, 2, \cdots, 2^{L}-1\}$

实际问题空间：（Issue Space）对于实际问题中所有自变量向量所组成的空间，记为 $S_I$

实际问题目标函数：（Issue function）目标就是寻找最优解使得该函数值最大，记为 $G:S_I\rightarrow \mathbb R$ ，（右侧其实不一定必须是实数空间，可以是任意的有序集）

基因转换函数：（Transition function for Gene）将基因转化为对应的实际问题中所对应的自变量向量（这是一个双射），记为 $f:S\rightarrow S_I$

适应度量化函数：（Adaptation function）用于评判一个基因在自然环境下的适应程度， $F:S_I\rightarrow \mathbb R_{ > 0}$ ，注意 $F(f(x))$ 一定是非负实数

适应度函数取值

$F(f(x))$ 函数一般有三种取法：

直接法

F(f(x)) = G(f(x))

要求 $G(f(x)) \subset \mathbb R_{ > 0}$

界限构造法

F(f(x)) = \begin{cases} G(f(x)),& f(x) < c;\\ 0,&\text{otherwise}. \end{cases}

对最大值有上限 $c$ 的限制。

倒数法

F(f(x)) = \frac{1}{c - G(f(x))}\quad \text{and}\quad c-G(f(x)) > 0

根据反比例函数图像知，该取法可以使得较大的值收敛的更快。

自然选择 Choose

基因的筛选：每一代下来，基因会发生筛选，依据适应度函数的大小，越大的选取到的概率越大，进入到下一代的概率也就越大，于是可以如下定义筛选概率：

P(x_i) = \frac{F(f(x_i))}{\sum_{i=1}^NF(f(x_i))}

选择算法：使用轮盘赌选择法（区段选择），将每一个概率视为 $[0,1]$ 区间上的一个区段，每次在其中随机一个数字，通过数字所处的区段，判断选择的基因。（可以通过前缀和，二分实现）

一些可能能用的优化：（没试过）

稳态繁殖：用部分优质新的基因更新父基因
没有重串的稳态繁殖：在稳态繁殖的基础上，基因序列两两不同。

基因重组 Recombination

基因重组，对应的就是二进制串数据的交换，设该事件发生的概率为 $R$ ，取值一般为 $0.4\sim 0.9$ ，这里只给出一种交叉方法：

单点交叉：交换两个基因的二进制串的最后 $m$ 位，这里的 $m$ 是在 $[1, L]$ 中随机的整数，其中 $L$ 为二进制的位数

x1 = 100110101
x2 = 110011100
若 m = 4 则单点交叉后为
x1' = 100111100
x2' = 110010101
使用位运算可以非常简单的完成此操作

基因突变 Mutation

基因突变，对应的就是二进制串上某一位从1变为0或者从0变为1，设该事件发生的概率为 $M$ ，取值一般为 $0.001\sim 0.1$ ，突变方法：

将单个基因中第 $m$ 位（从右向左数）对 $1$ 异或，其中 $m$ 为 $[1,L]$ 中的随机整数，其中 $L$ 为二进制的位数

x = 001001
若 m = 3 则基因突变后为
x' = 001101

初始化

所有要初始化的变量全部列出来了（并给出推荐取值）：

const int N = 20 ~ 500; // 种群规模（有时候越大越好）
const int T = 100 ~ 500; // 迭代次数
const int L = 22; // 二进制串的长度（取决于实际问题）
const double R = 0.4 ~ 0.9; // 重组概率
const double M = 0.001 ~ 0.1; // 突变概率

遗传过程

在基因空间 $S$ 上随机分布产生第一代种群。
计算适应值 $F(f(x))$ ，并给出选择概率。
顺次进行选择、交叉、突变三个步骤生成下一代种群，后面两个步骤要满足其发生的概率。
循环步骤2，步骤3，直到达到迭代次数或者达到目标解，退出循环，输出结果。

例子 - 求解函数最大值

求解函数

f(x) = x\sin(10\pi x) + 2

在 $[-1, 2]$ 上的最大值，其图像参考 GeoGebra - GA练习1。

如果精度要达到6位小数，则应该将 $[-1,2]$ 进行 $3\cdot 10^6$ 等分，则至少要 $log_2(3\cdot 10^6) = 21.516531 < 22$ ，则 $L = 22$ ，代码中详细描述了计算的过程：

点击显/隐代码

#include <bits/stdc++.h>
#define db double
#define ll long long
#define int ll
#define vi vector<int>
#define vii vector<vi >
#define pii pair<int, int>
#define vp vector<pii >
#define vip vector<vp >
#define mkp make_pair
#define pb push_back
#define Case(x) cout << "Case #" << x << ": "
using namespace std;
const int INF = 0x3f3f3f3f;
const int N = 300; // Size of Population
const int T = 200; // Number of iterations
const int L = 22; // Length of binary
const double R = 0.75; // Rate of recombination
const double M = 0.05; // Rate of mutation
double F(double x) { // Adaptation value (non-negative)
	if (x > 3e6) return 0;
	x = x / 1e6 - 1;
	return x * sin(10 * M_PI * x) + 2;
}
double getrand() { return 1.0 * rand() / RAND_MAX; }
pair<db, db> GA(int Num) {
	vi p; // Population
	for (double i = 0; i <= 3; i += 3e6 / N) { // initialization
		p.pb(i);
	}
	for (int _i = 0; _i < T; _i++) { // Genetic Algorithm
		db sum = 0; // Sum of Adaptation
		vector<db> a(N); // Adaptation & Probability for individual
		for (int i = 0; i < N; i++) {
			a[i] = F(p[i]);
			sum += a[i];
		}
		for (int i = 0; i < N; i++) {
			a[i] /= sum;
			a[i] += i ? a[i-1] : 0;
		}
		vi nt; // next generation
		for (int i = 0; i < N; i++) { // choose
			double r = getrand();
			nt.pb(p[lower_bound(a.begin(), a.end(), r) - a.begin()]);
		}
		// Recombination
		vi part(N); // partner
		for (int i = 0; i < N; i++) part[i] = i;
		random_shuffle(part.begin(), part.end());
		for (int i = 0; i < N; i += 2) {
			if (getrand() <= R) { // start
				int d = rand() % L + 1;
				int *i1 = &nt[part[i]], *i2 = &nt[part[i+1]];
				int j1 = (*i1)&((1<<d)-1), j2 = (*i2)&((1<<d)-1);
				*i1 += j2 - j1;
				*i2 += j1 - j2;
			}
		}
		// Mutation
		for (int i = 0; i < N; i++) {
			if (getrand() <= M) {
				int pos = rand() % L; // position of mutation
				nt[i] ^= (1 << pos);
			}
		}
		p = nt; // goto next generation
	}
	double mx = 0, best;
	for (int i = 0; i < N; i++) {
		if (F(p[i]) > mx) {
			mx = F(p[i]);
			best = p[i] / 1e6 - 1;
		}
	}
	cout << "Num" << Num << " mx = " << mx << ", best = " << best << '\n';
	return mkp(mx, best);
}
signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	srand(time(NULL));
	int TOT = 30;
	pair<db, db> best = {0, 0};
	for (int _i = 1; _i <= TOT; _i++) { 
		best = max(best, GA(_i));
	}
	cout << "mx = " << best.first << '\n' << "best = " << best.second << '\n';
	return 0;
}

通过这个例题，可以发现，多次重启问题是解决收敛至局部最优解的一个重要方法，而且增大种群总量也能提高达到全局最优解的概率。

例子 - TSP（旅行商问题）

经典NP问题，设地图上 $N$ 个城市（编号从 $1\sim N$ ），规划路线使得每个城市都有且仅经过一次，最后回到出发的城市，求最短路径。

在此题中，一个基因代表一种路径，那么基因就不能用二进制表示了，而是 $N$ 进制，每个基因都是 $N$ 的一个排列，这样就保存了一条路径上的所有信息了。

适应值函数

F(f(x)) = \frac{1}{G(f(x))}

其中 $G(f(x))$ 表示 $f(x)$ 这条路径的长度，为了转化为求最大解问题，故取倒数。

交叉算法（有序交叉）

此处不能再是简单的交换，因为这样就不能保证仍然是排列了。具体方法还是随机出一段序列，两个基因中保持这一段序列保持不动，将其余部分重组（通过一个例子解释下）：

012|3456|789
429|0853|176
两个竖杠之间的保持不变，左右两部分重组
先直接考虑将第二个序列中的值直接转移到第一个序列中，
如果和不变的值相重，则取其对应第二个序列的值，
若仍有重复，则继续重复，直到没有重复为止，
下面举出第一个序列中左右部分重组过程：
0->4->8
1->2
2->9
7->1
8->7
9->6->3->0
所以第一个序列最终为
829|3456|170
第二个同理可得
612|0853|749

突变算法（倒置变异法）

随机一段序列，将其倒置即可，比如：

012|3456|789
突变后为
012|6543|789

操作定义完成，开始打代码~

点击显/隐代码

#include <bits/stdc++.h>
#define db double
#define ll long long
#define int ll
#define vi vector<int>
#define vii vector<vi >
#define vd vector<db>
#define vdd vector<vd >
#define pii pair<int, int>
#define pdd pair<db, db>
#define vpd vector<pdd >
#define vipd vector<vpd >
#define vp vector<pii >
#define vip vector<vp >
#define mkp make_pair
#define pb push_back
#define Case(x) cout << "Case #" << x << ": "
using namespace std;
const int INF = 0x3f3f3f3f;
const int N = 500; // Size of Population
const int T = 500; // Number of iterations
int L; // Length of binary (Number of Cities)
const double R = 0.4; // Rate of recombination
const double M = 0.01; // Rate of mutation
vpd city;
double dis(pdd &x, pdd &y) { // Calculation Distance
	return sqrt((x.first - y.first) * (x.first - y.first) + (x.second - y.second) * (x.second - y.second));
}
double f(vi &x) { // Calculation Route Distance
	double ret = 0;
	for (int i = 0; i < L; i++) {
		ret += dis(city[x[i]], city[x[(i+1)%L]]);
	}
	return ret;
}
double F(vi &x) { // Adaptation value (non-negative)
	return 1/f(x);
}
double getrand() { return 1.0 * rand() / RAND_MAX; } // get a random num in [0,1]
pii randrange() { // get a random range [l,r] subset of [0,L)
	int l = rand() % L, r = rand() % L;
	while (l == r) l = rand() % L, r = rand() % L;
	if (l > r) return mkp(r, l);
	return mkp(l, r);
}
vi Swap(vi &i1, vi &i2, pii seg) { // Swap i2 to i1, return i1'
	int l = seg.first, r = seg.second;
	vi ret = i1, mp(L, -1);
	for (int i = l; i <= r; i++) mp[i1[i]] = i2[i];
	for (int i = 0; i < L; i++) {
		if (i >= l && i <= r) continue;
		int t = i2[i];
		while (mp[t] != -1) t = mp[t];
		ret[i] = t;
	}
	return ret;
}
pair<db, vi> GA(int Num) {
	vi perm(L); // A Permutation uses for random
	for (int i = 0; i < L; i++) perm[i] = i;
	vii p(N); // Population
	for (int i = 0; i < N; i++) { // initialization
		random_shuffle(perm.begin(), perm.end());
		p[i] = perm;
	}
	for (int _i = 0; _i < T; _i++) { // Genetic Algorithm
		double sum = 0; // Sum of Adaptation
		vector<db> a(N); // Adaptation & Probability for individual
		for (int i = 0; i < N; i++) {
			a[i] = F(p[i]);
			sum += a[i];
		}
		for (int i = 0; i < N; i++) {
			a[i] /= sum;
			a[i] += i ? a[i-1] : 0;
		}
		vii nt; // next generation
		for (int i = 0; i < N; i++) { // choose
			double r = getrand();
			nt.pb(p[lower_bound(a.begin(), a.end(), r) - a.begin()]);
		}
		// Recombination
		vi part(N); // partner
		for (int i = 0; i < N; i++) part[i] = i;
		random_shuffle(part.begin(), part.end());
		for (int i = 0; i < N; i += 2) {
			if (getrand() <= R) { // start
				pii seg = randrange(); // fixed segment
				vi i1 = Swap(nt[part[i]], nt[part[i+1]], seg);
				vi i2 = Swap(nt[part[i+1]], nt[part[i]], seg);
				nt[part[i]] = i1, nt[part[i+1]] = i2;
			}
		}
		// Mutation
		for (int i = 0; i < N; i++) {
			if (getrand() <= M) {
				pii seg = randrange(); // reverse segment
				reverse(nt[i].begin() + seg.first, nt[i].begin() + seg.second + 1);
			}
		}
		p = nt; // goto next generation
	}
	double mx = 0;
	vi best;
	for (int i = 0; i < N; i++) {
		if (F(p[i]) > mx) {
			mx = F(p[i]);
			best = p[i];
		}
	}
	return mkp(mx, best);
}
void init() { // Initialization
	freopen("30points.in", "r", stdin);
	cin >> L;
	city = vpd(L);
	for (int i = 0; i < L; i++) {
		int id;
		cin >> id >> city[i].first >> city[i].second;
	}
}
signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	srand(time(NULL));
	init();
	int TOT = 6000;
	pair<db, vi> best = {0, vi(1)};
	for (int _i = 1; _i <= TOT; _i++) { 
		pair<db, vi> t = GA(_i);
		if (t.first > best.first) best = t;
	}
	cout << "dis = " << f(best.second) << '\n';
	for (int i = 0; i <= L; i++) {
		vi id = best.second;
		cout << city[id[i%L]].first << ' ';
	}
	cout << '\n';
	for (int i = 0; i <= L; i++) {
		vi id = best.second;
		cout << city[id[i%L]].second << ' ';
	}
	cout << '\n';
	return 0;
}

30个点的数据

点击显/隐数据

最佳计算效果图：计算结果

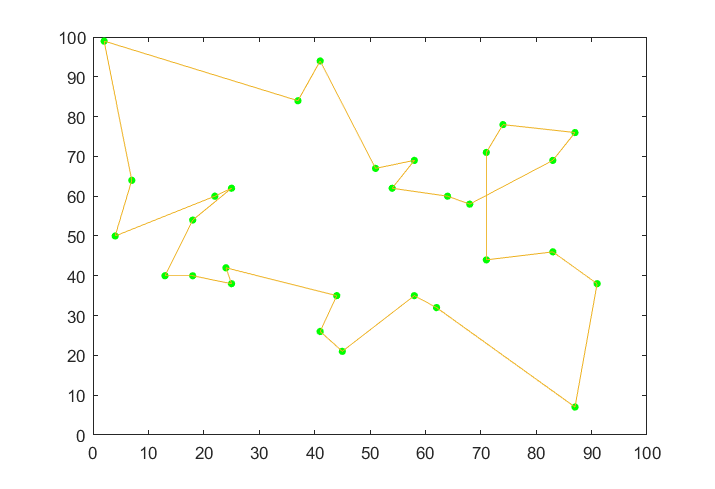
最优结果为424.78，这个GA算法最优结果为449.132，效果还行，但这个是多次计算后的最优值，应该还可以提升，小数据效果不错，但城市增加估计就很难保持精度了，于是考虑能否结合其他算法一起作用提高精度。

点击显/隐结果

13 18 25 24 44 41 45 58 62 87 91 83 71 71 74 87 83 68 64 54 58 51 41 37 2 7 4 22 25 18 13
40 40 38 42 35 26 21 35 32 7 38 46 44 71 78 76 69 58 60 62 69 67 94 84 99 64 50 60 62 54 40

这种路线，距离为449.132

MATLAB 绘图代码为

点击显/隐代码

fid = fopen('30.in', 'r');
n = fscanf(fid, '%d', 1);
A = fscanf(fid, '%f', [3,n]);

for i = 1 : n
    plot(A(2, i),A(3,i),'.','Color','g','MarkerSize',15);
    hold on;
end
x = fscanf(fid, '%d', 1);
for i = 1 : x
    m = fscanf(fid, '%d', 1);
    X = fscanf(fid, '%f', m);
    Y = fscanf(fid, '%f', m);
    plot(X, Y);
end
fclose(fid);

输入数据格式为

点击显/隐数据

30
1 18 54
2 87 76
3 74 78
4 71 71
5 25 38
6 58 35
7 4 50
8 13 40
9 18 40
10 24 42
11 71 44
12 64 60
13 68 58
14 83 69
15 58 69
16 54 62
17 51 67
18 37 84
19 41 94
20 2 99
21 7 64
22 22 60
23 25 62
24 62 32
25 87 7
26 91 38
27 83 46
28 41 26
29 45 21
30 44 35
1
31
13 18 25 24 44 41 45 58 62 87 91 83 71 71 74 87 83 68 64 54 58 51 41 37 2 7 4 22 25 18 13
40 40 38 42 35 26 21 35 32 7 38 46 44 71 78 76 69 58 60 62 69 67 94 84 99 64 50 60 62 54 40

数学建模

#随机算法

遗传算法的基本原理及代码

https://wty-yy.github.io/posts/25104/

作者

wty

发布于

2022年1月26日

许可协议

BP神经网络算法的基本原理及C++实现上一篇

对长江江豚迁地保护种群数量的预测基于Leslie和Logistic模型下一篇