BP神经网络算法的基本原理及C++实现

通过三天的折腾，总算把神经网络的C代码写出来了（用C写纯属因为我对它更熟悉一些，虽然现在基本人工智能算法都是Python写的，但C++快呀😆）（主要还是对Python不熟练，以后有时间应该用Python重写一遍），代码270行左右（对自己也是一次对代码熟练度的训练），使用BP(Back Propagation)神经网络，学习算法为随机梯度下降法

支持多线程学习（保证跑满CPU，GPU算法还没研究），支持学习中断、继承学习（程序运行到一半可以直接关闭，当前网络数据均已保存，可作为下次学习开始的数据）

先在识别手写数字上进行了应用。

对神经网络的介绍和理解，我都是从 3B1B - 深度学习系列视频 中学习的，本文中很多图片也是从该视频中截取出来的（他做的图示效果太好了😍），BP神经网络和深度学习本质没有很大的区别，就换个名字罢了，BP的含义是通过Back Propagation这个方法，优化整个网络参数，使得最终的结果更接近我们的目标值。（Back propagation方法下文会细讲）

本文主要研究数学计算部分，也就是上述视频的 Part3 - P2 部分的内容，推导公式，也就是整个算法最核心的东西“梯度下降法”。

神经网络基本原理

一个神经网络，是由很多层组成，每一层又有很多的结点（神经元），相邻的两层之间的所有结点两两连接（轴突），这样一个神经网络就建成了，如下图：

记一个神经网络的层数为 $L$。

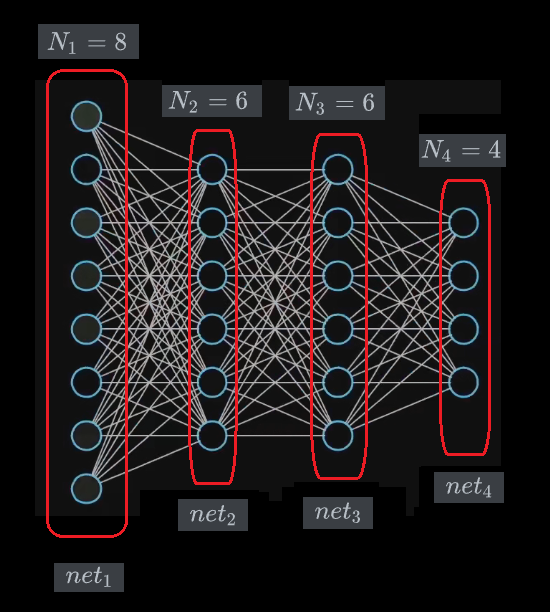
比如这个神经网络，$L = 4$，就由4层构成，分别记为 $net_1,net_2,net_3,net_4$，每一层中的结点数分别为 $N_1,N_2,N_3,N_4$ 个。

将神经网络的第一层 $net_1$ 称为 输入层， 最后一层 $net_L$ 称为 输出层。

网络的设计

输入层：根据输入数据的要求，比如一张手写数字照片，就是由 $28\times 28$ 的像素矩阵构成，矩阵中每个点在 $0~255$ 之间表示灰度值，那么如果将这个矩阵拉成一行，即 $28\cdot 28 = 784$，那么对于识别图像的问题而言，输入层就要有 $784$ 个结点，即 $N_1 = 784$。

输出层：根据输出数据的要求，比如一张手写数字，必定会对应一个 $0\sim 9$ 之间的数字，那么输出层就要在 $0\sim 9$ 之间做出选择，于是输出层就要有 $10$ 个结点，即 $N_L = 10$。

隐含层：除去第一层和最后一层，即 $2\sim L-1$ 这些层的结点个数完全由你来定，没有强制性要求，但至少要有一层，即 $L \geqslant 3$。

下面以手写数字的神经网络结构为例：

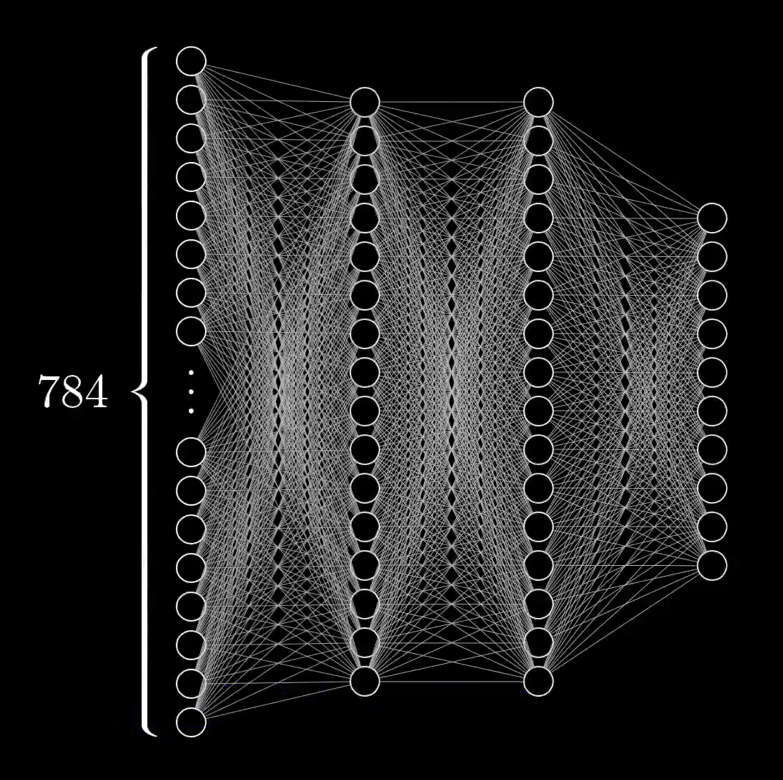
在这个神经网络中，$L = 4,\ N_1=784,\ N_2 = 16,\ N_3 = 16,\ N_4 = 10$。

可变参数

现在我们已经确定下了网络的结构，下一步确定所有的参数。

将第 $l$ 层的第 $i$ 个结点（从上到下）附上点权 $a_i^{(l)}$，并称之为该点的 激活值(activation)。（与神经细胞间电信号强度相对应）

将第 $l$ 层的第 $i$ 个结点（从上到下）附上点权 $b_i^{(l)}$，并称之为该点的 偏置(bias)。（与神经细胞产生电信号的阈值相对应）

将连接第 $l-1$ 层的第 $j$ 个结点和第 $l$ 层的第 $i$ 个结点的边附上边权 $w_{ij}^{(l)}$，并称之为该边的 权重。（与两个神经细胞间连接的强弱相对应，权值越大促进越强，权值越小抑制越强）

这三个参数中只有 偏置 和 权重 这两个是我们需要调参的（也就是神经网络需要调整的参数），激活值 是可以根据输入数据递推出来的（后文会细讲）。

现在简单计算一下，一共要调多少个参数：

$$\sum_{l=2}^{L}N_{l-1}\cdot N_l + N_l = \sum_{l=2}^{L}(N_{l-1}+1)\cdot N_l$$

对于上面设计的识别手写数字的网络为例，需要调整的参数个数为：

$$(784+1)\cdot 16+(16+1)\cdot 16+(16+1)\cdot 10 = 13002$$

这个参数个数确实有点哈人😢，这也就是计算学习时间长的原因；梯度下降法 就是一种调整这 $13002$ 个参数的一个算法（下文会详细解释）。

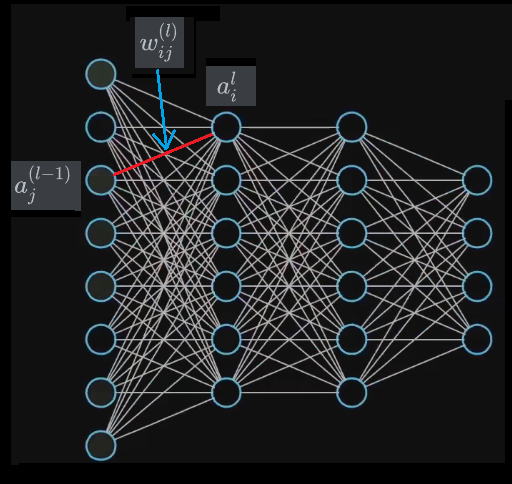
仔细看，可能发现 $w_{ij}^{(l)}$ 的下标 $ij$ 是不是写反了（应该从左到右然，而是从右到左），其实不然，我们把上述变量，以每一层为单位，以矩阵的形式写出来，这样下标就和矩阵对应上了。

$$a^{(l)} = \left[\begin{matrix} \ a_1^{(l)}&\cdots&a_{N_l}^{(l)}\ \end{matrix}\right]^{T}$$

$$b^{(l)} = \left[\begin{matrix} \ b_1^{(l)}&\cdots&b_{N_l}^{(l)}\ \end{matrix}\right]^{T}$$

$$w^{(l)} = \left[\begin{matrix} w_{11}^{(l)}&w_{12}^{(l)}&\cdots&w_{1,N_{l-1}}^{(l)}\\ w_{21}^{(l)}&w_{22}^{(l)}&\cdots&w_{2,N_{l-1}}^{(l)}\\ \vdots&\vdots&\ddots&\vdots\\ w_{N_l,1}^{(l)}&w_{N_l,2}^{(l)}&\cdots&w_{N_l,N_{l-1}}^{(l)}\\ \end{matrix}\right]_{(N_l\times N_{l-1})}$$

写成矩阵的形式当然是为了方便后续转移操作了~

$$$$

激活函数

接下来要引入一个激活函数，用于计算激活值，比较常用的函数是 \test{Sigmoid} 函数，即 \test{S} 型函数。

$$f(x) = \frac{1}{1+e^{-x}}$$

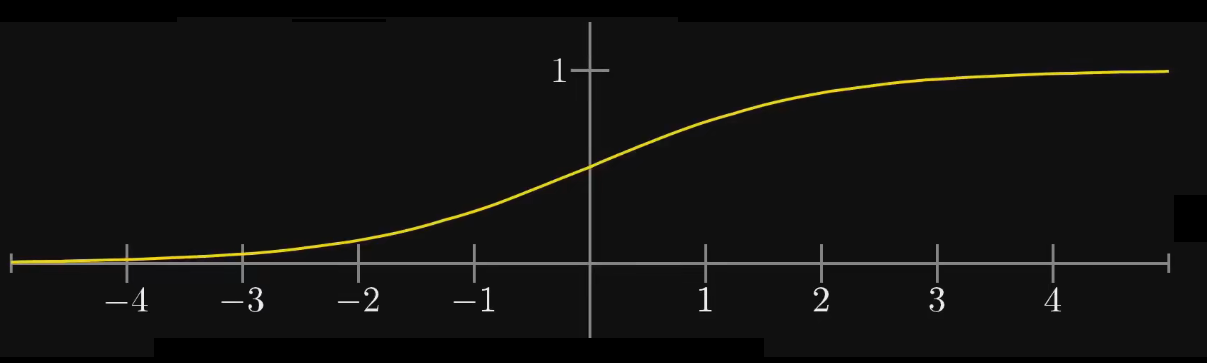
而现在用的更多的应该是 $\text{ReLU}$ 线性整流函数（Rectified Linear Unit）

$$\text{ReLU}(x) = \max(0,a)$$

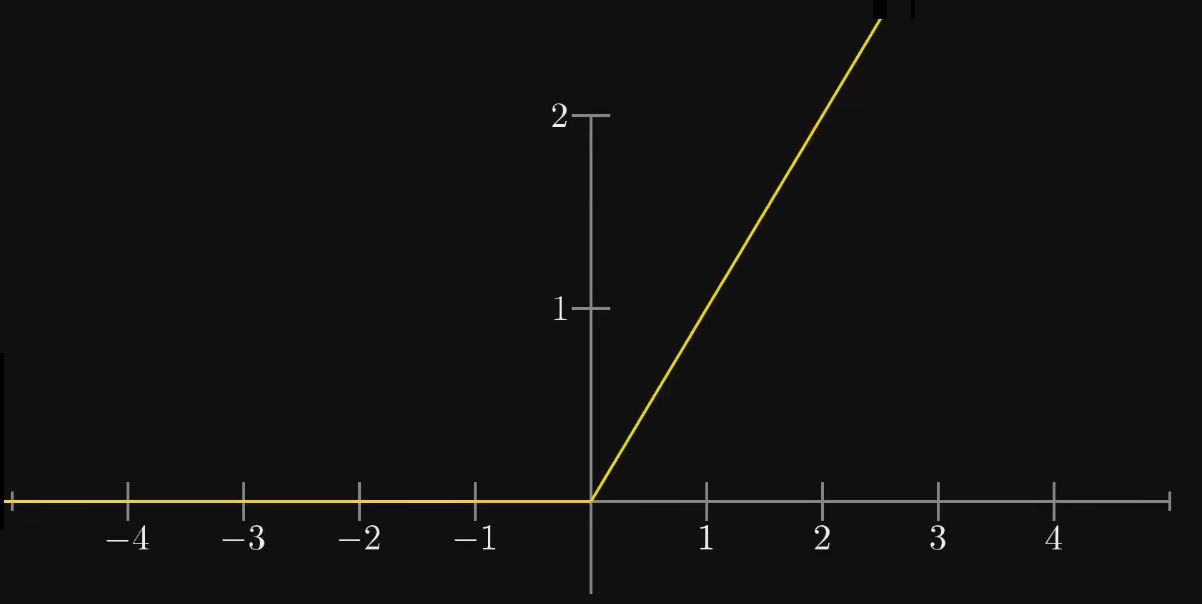
但在下面识别手写数字应用中我还是用的是 $\text{Sigmoid}$ 函数~

定义，函数作用在矩阵上，即作用在矩阵中的每一个元素上：

$$\begin{aligned} &Let\ A = \left[\begin{matrix} a_{11}&\cdots&a_{1m}\\ \vdots&\ddots&\vdots\\ a_{n1}&\cdots&a_{nm} \end{matrix}\right]\\ &Denote\ f(A) := \left[\begin{matrix} f(a_{11})&\cdots&f(a_{1m})\\ \vdots&\ddots&\vdots\\ f(a_{n1})&\cdots&f(a_{nm}) \end{matrix}\right] \end{aligned}$$

递推计算激活值

由于第 $l$ 层的每一个激活值，都与 $l-1$ 层的所有激活值相关，所以计算 $l$ 层的第 $i$ 个激活值，即将第 $l-1$ 的的所有激活值与它连接的边做加权之和，再加上该点的偏置，最后套上激活函数即可，下面这个图形象的阐述了这个过程，并表现出了和矩阵的联系。

与神经元是否激发相对应，当前神经元接收与它连接的神经元的信息，这些信息进行汇总后，先减去当前神经元的阈值后，再通过一个激活函数，最后判断自己是否需要激发。

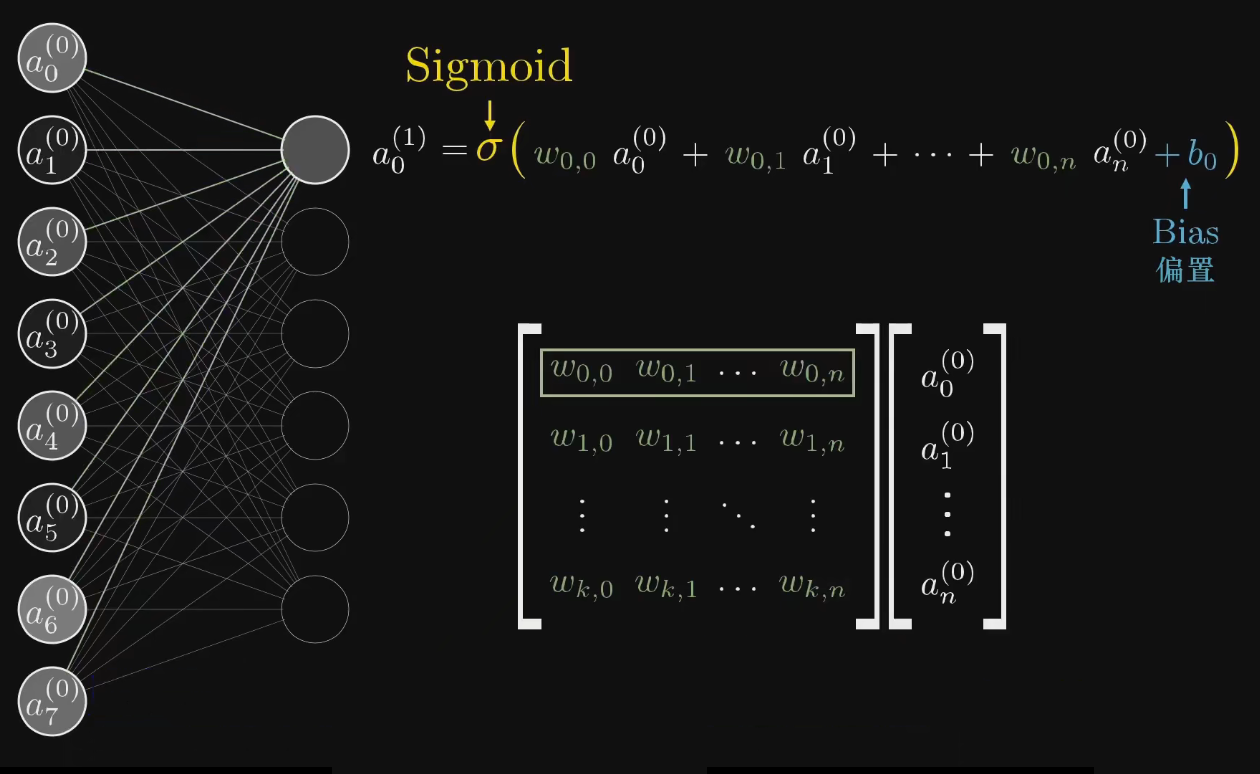
根据上述定义，不难写出每后面 $L-1$ 层的激活值的递推式

$$a^{(l)} = f(w^{(l)}a^{(l-1)}+b^{(l)})\quad (2\leqslant l\leqslant L)$$

计算单个样本的代价（误差）

现在我们已经可以通过第一层的激活值（输入层），计算后面每一层的激活值了，当计算到最后一层（输出层）时，正向递推结束。

对于当前这个网络和给定样本，我们就可以通过输出层激活值最大的点的编号，作为这个网络对该样本的输出。

那么很可能出现输出层数据混乱与目标值完全不相关的情况，那么这就是接下来，也是最重要的部分——参数优化，即通过调整 $w, b$ 参数，从而使得输出层的数据与目标值接近，最终对于一个完全没见过的样本，同样也能给出正确的结果，达到深度学习的要求。

那么，就先要描述输出层和目标值的误差大小，令目标值为

$$y = \left[\begin{matrix} \ y_1&\cdots&y_{N_L}\ \end{matrix}\right]^{T}$$

比如，以识别数字为例，每一张图片对应了一个数字，这个数字就是目标，令该数字为 $m$，因为输出层是以激活值最大的点为输出结果的，那么目标值就可以设置为

$$\begin{aligned} y =&\ \left[\begin{matrix}\ 0&\cdots&0&1&0&\cdots&0\ \end{matrix}\right]^{T}& \text{第}m\text{维为}1,\text{其他为}0\\ =&\ \left[a_{ij}\right]_{(N_L\times 1)},&\text{其中}a_{ij} = \delta_{im} \end{aligned}$$

其中

$$\delta_{ij} = \begin{cases} 1,&i=j\\ 0,&i\neq j \end{cases}$$

接下来定义输出层的激活值和目标值的误差大小，这里将其称为 代价（Cost）（也有叫做Loss的，“损失/误差”），方法就是简单的方差形式（由于不是线性形式，无法表示成矩阵形式）：

$$C = \sum_{i=1}^{N_L}(a_{i}^{(L)}-y_i)^2$$

梯度下降法

这个也就是整个BP神经网络算法最核心的部分

考虑如何将 $C$ 减小。由于每个参数 $w,b$ 对 $C$ 的影响各不相同（有的 $w$ 变化一点，$C$ 变化非常大，而有的则反之，所以每一个参数变化的大小肯定是不同的），而且如果只针对一个样本，参数变化过大，可能对另一个样本计算结果，发现变得更差了。那么如何寻找一个平衡参数使得每个样本的代价都打到最小，就是梯度下降法解决问题。

我们可以将 $C$ 视为一个因变量， $w, b$ 作为自变量：

$$C = C(w_{11}^{(2)},w_{12}^{(2)},\cdots,b_1^{(2)}\cdots,w_{11}^{(L)},w_{12}^{(L)},\cdots,b_1^{(L)},\cdots)$$

那么 $C$ 就可以视为一个 $n$ 维函数，由于中间的关系都是线性的，$\text{Sigmoid}$ 函数也是连续的（$\text{ReLU}$ 函数分段连续），所以 $C$ 是一个连续可微函数，我们考虑如何变化这些自变量，使得因变量 $C$ 减小地最快。

由于函数在导数方向上增大速度最快，$n$ 维函数在梯度的方向上增大速度最快，于是考虑 $C$ 的梯度：

$$\nabla C = \left[\begin{matrix} \ \dfrac{\partial C}{\partial w_{11}^{(2)}}&\dfrac{\partial C}{\partial w_{12}^{(2)}}&\cdots&\dfrac{\partial C}{b_1^{(2)}}\cdots&\dfrac{\partial C}{w_{11}^{(L)}}&\dfrac{\partial C}{w_{12}^{(L)}}&\cdots&\dfrac{\partial C}{\partial b_1^{(L)}}&\cdots\ \end{matrix}\right]^{T}$$

由于我们要使得 $C$ 减小速度最快，所以梯度的反方向就是每一个自变量的变化方向，于是现在问题转化为求解 $\nabla C$，这是一个递推的过程：

为方便书写做出如下的定义

以下的定义和推导均是我自己计算的，不能保证正确性，建议自己尝试先推一遍（但最后编码实现后，发现学习效果不错😉）

令 $z^{(l)} = w^{(l)}a^{(l-1)}+b^{(l)}$，则 $a^{(l)} = f(z^{(l)})$。

令 $f:\mathbb R^n\rightarrow \mathbb R$ 为连续可导函数，$A$ 的元素均为 $f$ 的变量，定义偏导数作用在矩阵上，即作用在矩阵中的每一个元素上，还定义了两个同阶矩阵之间的“点乘” $\odot$ 关系，即对应位上的元素相乘（这些符号下面都会用到，用于简化运算）：

$$\begin{aligned} &Let\ A = \left[\begin{matrix} a_{11}&\cdots&a_{1m}\\ \vdots&\ddots&\vdots\\ a_{n1}&\cdots&a_{nm} \end{matrix}\right], \ B = \left[\begin{matrix} b_{11}&\cdots&b_{1m}\\ \vdots&\ddots&\vdots\\ b_{n1}&\cdots&a_{nm} \end{matrix}\right]\\ &Denote\ \frac{\partial f}{\partial A} := \left[\begin{matrix} \frac{\partial f}{\partial a_{11}}&\cdots&\frac{\partial f}{\partial a_{1m}}\\ \vdots&\ddots&\vdots\\ \frac{\partial f}{\partial a_{n1}}&\cdots&\frac{\partial f}{\partial a_{nm}} \end{matrix}\right]\\ & Denote\ A\odot B := \left[\begin{matrix} a_{11}b_{11}&\cdots&a_{1m}b_{1m}\\ \vdots&\ddots&\vdots\\ a_{n1}b_{n1}&\cdots&a_{nm}b_{nm} \end{matrix}\right] \end{aligned}$$

先整理一下所有的式子（非矩阵形式，为了求偏导）：

$$\begin{cases} \displaystyle C = \sum_{i=1}^{N_L}(a_{i}^{(L)}-y_i)^2\\ \displaystyle z_i^{(l)} = \sum_{j=1}^{N_{l-1}}w_{ij}^{(l)}a_j^{(l-1)}+b_i^{(l)}\\ \displaystyle a_i^{(l)} = f(z_i^{(l)}) \end{cases}$$

下面开始求偏导，核心思想是利用 链式法则

先推第 $L$ 层的偏导

$$\frac{\partial C}{\partial a_i^{(L)}} = 2(a_i^{(L)} - y_i)$$

$$\begin{aligned} \frac{\partial C}{\partial b_i^{(L)}} =&\ \frac{\partial C}{\partial a_i^{(L)}}\cdot\frac{\partial a_i^{(L)}}{\partial z_i^{(L)}}\cdot\frac{\partial z_i^{(L)}}{\partial b_i^{(L)}}\\ =&\ 2(a_i^{(L)}-y_i)\cdot f'(z_i^{(L)})\cdot 1 \end{aligned}$$

$$\begin{aligned} \frac{\partial C}{\partial w_{ij}^{(L)}} =&\ \frac{\partial C}{\partial a_i^{(L)}}\cdot\frac{\partial a_i^{(L)}}{\partial z_i^{(L)}}\cdot\frac{\partial z_i^{(L)}}{\partial w_{ij}^{(L)}}\\ =&\ 2(a_i^{(L)}-y_i)\cdot f'(z_i^{(L)})\cdot a_j^{(L-1)} \end{aligned}$$

$$\begin{aligned} \frac{\partial C}{\partial a_j^{(L-1)}} =&\ \sum_{i=1}^{N_L} \frac{\partial C}{\partial a_i^{(L)}}\cdot\frac{\partial a_i^{(L)}}{\partial z_i^{(L)}}\cdot\frac{\partial z_i^{(L)}}{\partial a_j^{(L-1)}}\\ =&\ \sum_{i=1}^{N_L}2(a_i^{(L)}-y_i)\cdot f'(z_i^{(L)})\cdot w_{ij}^{(L)} \end{aligned}$$

等价的矩阵形式

$$\begin{aligned} \frac{\partial C}{\partial b^{(L)}} =&\ 2(a^{(L)}-y)\odot f'(z^{(L)})\\ \frac{\partial C}{\partial w^{(L)}} =&\ \left(2(a^{(L)}-y)\odot f'(z^{(L)})\right)\cdot\left(a^{(L-1)}\right)^T\\ \frac{\partial C}{\partial a^{(L-1)}} =& \left(w^{(L)}\right)^T\cdot\left(2(a^{(L)}-y)\odot f'(z^{(L)})\right) \end{aligned}$$

经过观察发现，后面两个式子中包含了第一个式子（还是很有意思的），于是

$$\begin{aligned} \frac{\partial C}{\partial b^{(L)}} =&\ 2(a^{(L)}-y)\odot f'(z^{(L)})\\ \frac{\partial C}{\partial w^{(L)}} =&\ \frac{\partial C}{\partial b^{(L)}}\cdot\left(a^{(L-1)}\right)^T\\ \frac{\partial C}{\partial a^{(L-1)}} =& \left(w^{(L)}\right)^T\cdot\frac{\partial C}{\partial b^{(L)}} \end{aligned}$$

类似的，有了 $\displaystyle\frac{\partial C}{\partial a^{(L-1)}}$，后面的项可以类比推出，于是整个偏导的递推式如下：

$$\begin{aligned} \frac{\partial C}{\partial b^{(l)}} =&\ \frac{\partial C}{\partial a^{(l)}}\odot f'(z^{(l)})\\ \frac{\partial C}{\partial w^{(l)}} =&\ \frac{\partial C}{\partial b^{(l)}}\cdot\left(a^{(l-1)}\right)^T\\ \frac{\partial C}{\partial a^{(l-1)}} =& \left(w^{(l)}\right)^T\cdot\frac{\partial C}{\partial b^{(l)}} \end{aligned}\quad (2\leqslant l\leqslant L)$$

递推初始值：$\displaystyle\frac{\partial C}{\partial a^{(L)}} = 2\left(a^{(L)}-y\right)$

于是就可以快乐的递推了🎉（核心部分结束）

随机分组更新

有了梯度值，就知道每一个样本对每一个参数调整的大小了，但是如果对每一个样本都进行一次调参，次数过多，而且可能导致参数迅速下降到某一个值上，导致无法获得全局最优值。

考虑能否将样本随机分为一组一组的，每一组为一个整体，计算一次梯度的平均值，最后再对网络参数进行一次修改，这就是随机梯度下降法的思路。

先将样本打乱，设定一个 $\text{Mini-batch}$ 大小，以一个 $\text{Mini-batch}$ 作为梯度下降的一步，对网络参数进行修改，如此反复进行迭代，从而使得代价函数收敛到一个局部最小值上。

初始化数据

初始值的设定十分重要，收敛速度和收敛效果和初始值关系很大，导致我前几天计算的精确度一致到不了 90%，最后修改后计算了不到20min精确度就到 94% 了。

最初网络的建立是没有任何参数的，所以都是 $w,b$ 都是随机产生的，当使用 $\text{Sigmoid}$ 函数时，在 $0$ 附近的导数值较大，而在远离 $0$ 的位置导数几乎为 $0$，所以将初始值设置在 $[-1,1]$ 之间（关键），收敛速度最快，效果很好。

神经网络C++实现

理论成立，开始实现

我喜欢把完成一整个 梯度下降法 的过程称为一次 学习😜，把当前的网络参数（主要是 $b,w$ 的值）称为当前的 学习成果。

样例数据的处理

这里以手写数字识别为例子，网上已有现成的数据集用于训练，如 Minist 就是一个很好的数据集，里面包含了 $60000$ 个训练数据， $10000$ 个测试数据。

但由于这些数据都是 Python 下的，为了使用 C++ 处理，所以需要先用 Python 进行解包，解包教程。

我是先把训练数据导出为两个文件，train.in 里面是一个 $60000\times 784$ 像素矩阵，矩阵每一行是由像素 $28\times 28$ 的图片拉伸成的，矩阵中每一个元素在 $[0,255]$ 之间，表示灰度值，train.out 是一个 $60000\times 1$ 的答案向量，对应 train.in 每一行的所对应的图像的数字。

test.in 是一个 $10000\times 784$ 像素矩阵，数据范围同 train.in，test.out 是一个 $10000\times 1$ 的答案向量，含义同 train.out，这个数据集用于对训练的网络进行测试，因为这些数据在 train.in 中没有出现过，可以通过对该数据集的测试判断网络的识别效果。

学习成果的保存

由于每一步的学习成果，是可以作为下次学习开始的数据的，所以需要在学习过程中保存下来，这里给出我设计的一个保存格式

L // 网络层数
N[0] N[1] ... N[L-1] // 每一层的结点个数
net[1].w // 网络第1层的w矩阵(N[1]*N[0])
net[1].b // 网络第1层的b矩阵(N[1]*1)
...
net[L-1].w // 网络最后一层的w矩阵(N[L-1]*N[L-2])
net[L-1].b // 网络最后一层的b矩阵(N[L-1]*1)

由于代码中的下标都是从 $0$ 开始的，所以 N[i] 对应上文中的常量 $N_{i+1}$，net[i].w 对应上文中的矩阵 $w^{(i+1)}$，net[i].b 对应上文中的矩阵 $b^{(i+1)}$。

矩阵实现

矩阵需要满足矩阵乘法、矩阵加法、矩阵乘常数、矩阵之间的点乘、矩阵的转置、矩阵的输出，这六个操作，以结构体方式完成，代码如下：

struct mat{ // Matrix Data Struct
	int n, m; // Size of Matrix : n * m
	vdd M;
	mat() {}
	mat(int n, int m, int num = 0) : n(n), m(m) { M = vdd(n, vd(m, num)); }
	mat operator * (const mat &y) const & { // multiply of Matrix
		assert(m == y.n);
		mat z(n, y.m);
		for (int i = 0; i < n; i++)
			for (int j = 0; j < y.m; j++)
				for (int k = 0; k < m; k++)
					z.M[i][j] += M[i][k] * y.M[k][j];
		return z;
	}
	mat operator + (const mat &y) const & { // addition of Matrix
		assert(n == y.n && m == y.m);
		mat z(n, m);
		for (int i = 0; i < n; i++)
			for (int j = 0; j < m; j++)
				z.M[i][j] = M[i][j] + y.M[i][j];
		return z;
	}
	mat operator * (const double &y) const & { // multiply Matrix and Const
		mat z(n, m);
		for (int i = 0; i < n; i++)
			for (int j = 0; j < m; j++)
				z.M[i][j] = M[i][j] * y;
		return z;
	}
	mat dot(mat &x, mat &y) { // dot multiplay of Matrix
		assert(x.n == y.n && x.m == y.m);
		int n = x.n, m = x.m;
		mat z(n, m);
		for (int i = 0; i < n; i++)
			for (int j = 0; j < m; j++)
				z.M[i][j] = x.M[i][j] * y.M[i][j];
		return z;
	}
	mat operator ~ () const & { // transpose the Matrix
		mat z(m, n);
		for (int i = 0; i < m; i++)
			for (int j = 0; j < n; j++)
				z.M[i][j] = M[j][i];
		return z;
	}
	void print() { // print the Matrix
		for (int i = 0; i < n; i++) {
			for (int j = 0; j < m; j++) {
				printf("%.2lf ", M[i][j]);
			}
			putchar('\n');
		}
		putchar('\n');
	}
}MAT;

代码实现

所有的代码和测试数据均上传至 Github - ANN—Writing-Number

代码有“一点”长（很考验耐心和准确性，就当在做一道大型OI模拟题了🤣），主要是矩阵的实现和输入输出部分比较复杂，核心部分只有50行左右。

对代码中的常量进行下解释，这样以后就只用修改这些值就可以用于其他功能了🙌：

const int T = 60000; // 总的样例数目
const int L = 4; // 网络的层数
const int IN = 784; // 输入层的结点个数，即N[0]
const int OUT = 10; // 输出层的结点个数，即N[L-1]
const int N[L] = {IN, 16, 16, OUT}; // 每一层的结点个数
db image[T][IN]; // 图像数据（输入数据）
int ans[T]; // 图像对应的数字（答案数据）
const int GROUP = 100; // 学习小组的大小（每个 Mini-batch 的大小）
const int NUM = 600; // 学习小组的个数（这里要求 NUM * GROUP = T）
const int TOT = 1500; // 对所有样例进行训练的次数（这里多线程下大概算一次60000个样例，需要1.5s）
const int THR = 20; // 线程数目

代码中有很多英文注释，助于理解。

这是第一份代码ANN.cpp，只能支持单线程学习

#include <bits/stdc++.h>
#define db double
#define ll long long
#define vi vector<int>
#define vii vector<vi >
#define vd vector<db>
#define vdd vector<vd >
#define pii pair<int, int>
#define pdd pair<db, db>
#define vpd vector<pdd >
#define vipd vector<vpd >
#define vp vector<pii >
#define vip vector<vp >
#define mkp make_pair
#define pb push_back
using namespace std;
const int INF = 0x3f3f3f3f;
const int T = 60000; // Number of Total training Data
const int L = 4; // Number of Layers (contains Input layer and Output layer)
const int IN = 784; // Number of Nodes in Layer 1 (Input Layer)
const int OUT = 10; // Number of Nodes in Layer L-1 (Output Layer)
const int N[L] = {IN, 16, 16, OUT}; // Number of Nodes in each Layer
//vd N(L); 
db image[T][IN]; // Image Data
int ans[T]; // Label of Image Data (Answer)
const int GROUP = 100; // Learning Group (Upgrade the network by GROUP numbers of Learning Data)
const int NUM = 600; // Number of Learning Group
const int TOT = 1; // Number of ANN
struct mat{ // Matrix Data Struct
	int n, m; // Size of Matrix : n * m
	vdd M;
	mat() {}
	mat(int n, int m, int num = 0) : n(n), m(m) { M = vdd(n, vd(m, num)); }
	mat operator * (const mat &y) const & { // multiply of Matrix
		assert(m == y.n);
		mat z(n, y.m);
		for (int i = 0; i < n; i++)
			for (int j = 0; j < y.m; j++)
				for (int k = 0; k < m; k++)
					z.M[i][j] += M[i][k] * y.M[k][j];
		return z;
	}
	mat operator + (const mat &y) const & { // addition of Matrix
		assert(n == y.n && m == y.m);
		mat z(n, m);
		for (int i = 0; i < n; i++)
			for (int j = 0; j < m; j++)
				z.M[i][j] = M[i][j] + y.M[i][j];
		return z;
	}
	mat operator * (const double &y) const & { // multiply Matrix and Const
		mat z(n, m);
		for (int i = 0; i < n; i++)
			for (int j = 0; j < m; j++)
				z.M[i][j] = M[i][j] * y;
		return z;
	}
	mat dot(mat &x, mat &y) { // dot multiplay of Matrix
		assert(x.n == y.n && x.m == y.m);
		int n = x.n, m = x.m;
		mat z(n, m);
		for (int i = 0; i < n; i++)
			for (int j = 0; j < m; j++)
				z.M[i][j] = x.M[i][j] * y.M[i][j];
		return z;
	}
	mat operator ~ () const & { // transpose the Matrix
		mat z(m, n);
		for (int i = 0; i < m; i++)
			for (int j = 0; j < n; j++)
				z.M[i][j] = M[j][i];
		return z;
	}
	void print() { // print the Matrix
		for (int i = 0; i < n; i++) {
			for (int j = 0; j < m; j++) {
				printf("%.2lf ", M[i][j]);
			}
			putchar('\n');
		}
		putchar('\n');
	}
}MAT;
struct layer { // Layer of the Network
	mat a, w, b, z;
	int id;
	layer() {}
	layer(int id) : id(id) {
		a = mat(N[id], 1);
		if (id) {
			w = mat(N[id], N[id-1]);
			b = mat(N[id], 1);
		}
	}
}baseNet[L]; // basic network
db getrand() { return 1.0 * rand() / RAND_MAX; }
void init() { // initialize Training Data
	freopen("train.in", "r", stdin);
	for (int i = 0; i < T; i++) {
		for (int j = 0; j < IN; j++) {
			scanf("%lf", &image[i][j]);
			image[i][j] /= 255;
		}
	}
	fclose(stdin);
	freopen("train.out", "r", stdin);
	for (int i = 0; i < T; i++) scanf("%d", &ans[i]);
	fclose(stdin);
	printf("Reading complete!\n");
	// image Input TEST
	//for (int i = 0; i < 784; i++) {
	//	printf("%d ", (int)(image[0][i] * 255));
	//	if ((i+1) % 28 == 0) {
	//		putchar('\n');
	//	}
	//}
	freopen("diary.out", "w", stdout);
	fclose(stdout);
}
void Save(int num) { // Print Learning Result
	string s = string("Result") + to_string(num) + string(".out");
	freopen(s.c_str(), "w", stdout);
	printf("%d\n", L);
	for (int i = 0; i < L; i++) printf("%d ", N[i]);
	putchar('\n');
	for (int l = 1; l < L; l++) {
		baseNet[l].w.print();
		baseNet[l].b.print();
	}
	fclose(stdout);
}
// Back Propagation (Learning)
mat f(mat &x) { // activate function (sigmoid)
	mat z(x.n, x.m);
	for (int i = 0; i < x.n; i++) {
		for (int j = 0; j < x.m; j++) {
			db t = x.M[i][j];
			z.M[i][j] = 1.0 / (1 + exp(-t));
		}
	}
	return z;
}
mat _f(mat &x) { // Derivative of activate function 
	mat z(x.n, x.m);
	for (int i = 0; i < x.n; i++) {
		for (int j = 0; j < x.m; j++) {
			db t = x.M[i][j];
			z.M[i][j] = 1.0 / (exp(t) + exp(-t) + 2);
		}
	}
	return z;
}
// Id of Learning Data and Total gradient
db BP(int id, layer grad[]) { // return Cost
	layer net[L];
	mat y(OUT, 1); // Desired result (Answer)
	for (int i = 0; i < L; i++) net[i] = baseNet[i];
	// initialize Input & Desired Data
	for (int i = 0; i < IN; i++) net[0].a.M[i][0] = image[id][i];
	for (int i = 0; i < OUT; i++)
		if (i == ans[id]) y.M[i][0] = 1;
	// Forward
	for (int l = 1; l < L; l++) {
		net[l].z = net[l].w * net[l-1].a + net[l].b;
		net[l].a = f(net[l].z);
	}
	// Backward
	mat dc_da = (net[L-1].a + (y * (-1))) * 2;
	for (int l = L-1; l >= 1; l--) {
		mat _fz = _f(net[l].z);
		mat dc_db = MAT.dot(dc_da, _fz);
		grad[l].b = grad[l].b + dc_db;
		grad[l].w = grad[l].w + (dc_db * (~net[l-1].a));
		dc_da = (~net[l].w) * dc_db;
	}
	// Cost
	db cost = 0;
	for (int i = 0; i < OUT; i++) cost += pow(net[L-1].a.M[i][0] - y.M[i][0], 2);
	return cost;
}
void ANN() { // Artificial Neural Network
	// initialize the struct of Network
	for (int i = 0; i < L; i++) baseNet[i] = layer(i);
	if (freopen("Result.in", "r", stdin) == NULL) { // initialize w and b randomly
		freopen("/dev/tty", "w", stdout);
		printf("Randomly initialization\n");
		for (int l = 1; l < L; l++) {
			for (int i = 0; i < N[l]; i++) {
				for (int j = 0; j < N[l-1]; j++)
					baseNet[l].w.M[i][j] = getrand() * 10 - 5;
				baseNet[l].b.M[i][0] = getrand() * 40 - 20;
			}
		}
	} else { // Using last Learning Data
		freopen("/dev/tty", "w", stdout);
		printf("Get Result.in\n");
		int rL;
		scanf("%d", &rL);
		assert(L == rL);
		vi rN(L);
		for (int i = 0; i < L; i++) {
			scanf("%d", &rN[i]);
			assert(rN[i] == N[i]);
		}
		for (int l = 1; l < L; l++) {
			for (int i = 0; i < N[l]; i++)
				for (int j = 0; j < N[l-1]; j++)
					scanf("%lf", &baseNet[l].w.M[i][j]);
			for (int i = 0; i < N[l]; i++)
				scanf("%lf", &baseNet[l].b.M[i][0]);
		}
		fclose(stdin);
	}
	vi perm(T);
	for (int i = 0; i < T; i++) perm[i] = i;
	int fg = 0; // id of Save data
	for (int _i = 0; _i < TOT; _i++) {
		random_shuffle(perm.begin(), perm.end());
		for (int i = 0; i < GROUP * NUM; i += GROUP) {
			layer grad[L]; // average gradient of a group
			for (int l = 0; l < L; l++) grad[l] = layer(l);
			db cost = 0; // average cost of a group
			for (int j = i; j < i + GROUP; j++) { // assign Learning tasks
				cost += BP(perm[j], grad);
			}
			for (int i = 1; i < L; i++) { // Upgrade Network
				baseNet[i].w = baseNet[i].w + grad[i].w * (-1.0 / GROUP);
				baseNet[i].b = baseNet[i].b + grad[i].b * (-1.0 / GROUP);
			}
			freopen("diary.out", "a", stdout);
			printf("%lf\n", cost / GROUP);
			fclose(stdout);
			Save(fg);
			fg ^= 1;
		}
		freopen("/dev/tty", "w", stdout);
		printf("complete turn: %d\n", _i+1);
	}
}
signed main() {
	srand(time(NULL));
	init();
	clock_t st = clock(), en;
	ANN();
	en = clock();
	freopen("diary.out", "a", stdout);
	printf("Learning time: %lf s\n", 1.0 * (en - st) / CLOCKS_PER_SEC);
	fclose(stdout);
	return 0;
}

这是第二个版本的代码ANN_Parallel.cpp，支持多线程（此代码是在 Linux 上运行的，如果要在 Windows 下运行，需要支持 thread 这个函数，方法可以见这篇博客 CSDN - mingw-w64安装支持c++11中thread（windows下））

#include <bits/stdc++.h>
#define db double
#define ll long long
#define vi vector<int>
#define vii vector<vi >
#define vd vector<db>
#define vdd vector<vd >
#define pii pair<int, int>
#define pdd pair<db, db>
#define vpd vector<pdd >
#define vipd vector<vpd >
#define vp vector<pii >
#define vip vector<vp >
#define mkp make_pair
#define pb push_back
using namespace std;
const int INF = 0x3f3f3f3f;
const int T = 60000; // Number of Total training Data
const int L = 4; // Number of Layers (contains Input layer and Output layer)
const int IN = 784; // Number of Nodes in Layer 1 (Input Layer)
const int OUT = 10; // Number of Nodes in Layer L-1 (Output Layer)
const int N[L] = {IN, 16, 16, OUT}; // Number of Nodes in each Layer
//vd N(L); 
db image[T][IN]; // Image Data
int ans[T]; // Label of Image Data (Answer)
const int GROUP = 100; // Learning Group (Upgrade the network by GROUP numbers of Learning Data)
const int TOT = 100000; // Number of ANN, 1 7s
const int THR = 8; // Number of Threads
struct mat{ // Matrix Data Struct
	int n, m; // Size of Matrix : n * m
	vdd M;
	mat() {}
	mat(int n, int m, int num = 0) : n(n), m(m) { M = vdd(n, vd(m, num)); }
	mat operator * (const mat &y) const & { // multiply of Matrix
		assert(m == y.n);
		mat z(n, y.m);
		for (int i = 0; i < n; i++)
			for (int j = 0; j < y.m; j++)
				for (int k = 0; k < m; k++)
					z.M[i][j] += M[i][k] * y.M[k][j];
		return z;
	}
	mat operator + (const mat &y) const & { // addition of Matrix
		assert(n == y.n && m == y.m);
		mat z(n, m);
		for (int i = 0; i < n; i++)
			for (int j = 0; j < m; j++)
				z.M[i][j] = M[i][j] + y.M[i][j];
		return z;
	}
	mat operator * (const double &y) const & { // multiply Matrix and Const
		mat z(n, m);
		for (int i = 0; i < n; i++)
			for (int j = 0; j < m; j++)
				z.M[i][j] = M[i][j] * y;
		return z;
	}
	mat dot(mat &x, mat &y) { // dot multiplay of Matrix
		assert(x.n == y.n && x.m == y.m);
		int n = x.n, m = x.m;
		mat z(n, m);
		for (int i = 0; i < n; i++)
			for (int j = 0; j < m; j++)
				z.M[i][j] = x.M[i][j] * y.M[i][j];
		return z;
	}
	mat operator ~ () const & { // transpose the Matrix
		mat z(m, n);
		for (int i = 0; i < m; i++)
			for (int j = 0; j < n; j++)
				z.M[i][j] = M[j][i];
		return z;
	}
	void print() { // print the Matrix
		for (int i = 0; i < n; i++) {
			for (int j = 0; j < m; j++) {
				printf("%.2lf ", M[i][j]);
			}
			putchar('\n');
		}
		putchar('\n');
	}
}MAT;
struct layer { // Layer of the Network
	mat a, w, b, z;
	int id;
	layer() {}
	layer(int id) : id(id) {
		a = mat(N[id], 1);
		if (id) {
			w = mat(N[id], N[id-1]);
			b = mat(N[id], 1);
		}
	}
}baseNet[L]; // basic network
db getrand() { return 1.0 * rand() / RAND_MAX; }
void init() { // initialize Training Data
	freopen("train.in", "r", stdin);
	for (int i = 0; i < T; i++) {
		for (int j = 0; j < IN; j++) {
			scanf("%lf", &image[i][j]);
			image[i][j] /= 255;
		}
	}
	fclose(stdin);
	freopen("train.out", "r", stdin);
	for (int i = 0; i < T; i++) scanf("%d", &ans[i]);
	fclose(stdin);
	printf("Reading complete!\n");
	// image Input TEST
	//for (int i = 0; i < 784; i++) {
	//	printf("%d ", (int)(image[0][i] * 255));
	//	if ((i+1) % 28 == 0) {
	//		putchar('\n');
	//	}
	//}
	freopen("diary.out", "w", stdout);
	fclose(stdout);
}
void Save(int num) { // Print Learning Result
	string s = string("Result") + to_string(num) + string(".out");
	freopen(s.c_str(), "w", stdout);
	printf("%d\n", L);
	for (int i = 0; i < L; i++) printf("%d ", N[i]);
	putchar('\n');
	for (int l = 1; l < L; l++) {
		baseNet[l].w.print();
		baseNet[l].b.print();
	}
	fclose(stdout);
}
// Back Propagation (Learning)
mat f(mat &x) { // activate function (sigmoid)
	mat z(x.n, x.m);
	for (int i = 0; i < x.n; i++) {
		for (int j = 0; j < x.m; j++) {
			db t = x.M[i][j];
			z.M[i][j] = 1.0 / (1 + exp(-t));
		}
	}
	return z;
}
mat _f(mat &x) { // Derivative of activate function 
	mat z(x.n, x.m);
	for (int i = 0; i < x.n; i++) {
		for (int j = 0; j < x.m; j++) {
			db t = x.M[i][j];
			z.M[i][j] = 1.0 / (exp(t) + exp(-t) + 2);
		}
	}
	return z;
}
// Id of Learning Data and Total gradient and cost
db BP(int id, layer grad[]) { // return Cost
	layer net[L];
	mat y(OUT, 1); // Desired result (Answer)
	for (int i = 0; i < L; i++) net[i] = baseNet[i];
	// initialize Input & Desired Data
	for (int i = 0; i < IN; i++) net[0].a.M[i][0] = image[id][i];
	for (int i = 0; i < OUT; i++)
		if (i == ans[id]) y.M[i][0] = 1;
	// Forward
	for (int l = 1; l < L; l++) {
		net[l].z = net[l].w * net[l-1].a + net[l].b;
		net[l].a = f(net[l].z);
	}
	// Backward
	mat dc_da = (net[L-1].a + (y * (-1))) * 2;
	for (int l = L-1; l >= 1; l--) {
		mat _fz = _f(net[l].z);
		mat dc_db = MAT.dot(dc_da, _fz);
		grad[l].b = grad[l].b + dc_db;
		grad[l].w = grad[l].w + (dc_db * (~net[l-1].a));
		dc_da = (~net[l].w) * dc_db;
	}
	// Cost
	db cost = 0;
	for (int i = 0; i < OUT; i++) cost += pow(net[L-1].a.M[i][0] - y.M[i][0], 2);
	return cost;
}
void GroupLearn(int st, vi *perm, layer grad[], db *cost) { // Thread of Group Learning with start id
	for (int j = st; j < st + GROUP; j++) { // assign Learning tasks
		*cost += BP((*perm)[j], grad);
	}
}
void ANN() { // Artificial Neural Network
	// initialize the struct of Network
	for (int i = 0; i < L; i++) baseNet[i] = layer(i);
	if (freopen("Result.in", "r", stdin) == NULL) { // initialize w and b randomly
		freopen("/dev/tty", "w", stdout);
		printf("Randomly initialization\n");
		for (int l = 1; l < L; l++) {
			for (int i = 0; i < N[l]; i++) {
				for (int j = 0; j < N[l-1]; j++)
					baseNet[l].w.M[i][j] = getrand() * 2 - 1; // rand in [-1,1] is better
				baseNet[l].b.M[i][0] = getrand() * 2 - 1;
			}
		}
	} else { // Using last Learning Data
		freopen("/dev/tty", "w", stdout);
		printf("Get Result.in\n");
		int rL;
		scanf("%d", &rL);
		assert(L == rL);
		vi rN(L);
		for (int i = 0; i < L; i++) {
			scanf("%d", &rN[i]);
			assert(rN[i] == N[i]);
		}
		for (int l = 1; l < L; l++) {
			for (int i = 0; i < N[l]; i++)
				for (int j = 0; j < N[l-1]; j++)
					scanf("%lf", &baseNet[l].w.M[i][j]);
			for (int i = 0; i < N[l]; i++)
				scanf("%lf", &baseNet[l].b.M[i][0]);
		}
		fclose(stdin);
	}
	vi perm(T);
	for (int i = 0; i < T; i++) perm[i] = i;
	int fg = 0; // id of Save data
	for (int _i = 0; _i < TOT; _i++) {
		random_shuffle(perm.begin(), perm.end());
		db Cost = 0;
		for (int i = 0; i < T; i += GROUP * THR) {
			layer grad[THR][L]; // average gradient of a group for each thread
			db cost[THR] = {0}; // average cost of a group
			thread th[THR];
			for (int t = 0; t < THR; t++)
				for (int l = 0; l < L; l++)
					grad[t][l] = layer(l);
			for (int t = 0; t < THR; t++) {
				th[t] = thread(GroupLearn, i + t * GROUP, &perm, grad[t], &cost[t]);
			}
			for (int t = 0; t < THR; t++) {
				th[t].join();
			}
			for (int i = 1; i < L; i++) { // Upgrade Network
				for (int t = 1; t < THR; t++) {
					grad[0][i].w = grad[0][i].w + grad[t][i].w;
					grad[0][i].b = grad[0][i].b + grad[t][i].b;
				}
			}
			for (int i = 1; i < L; i++) {
				baseNet[i].w = baseNet[i].w + grad[0][i].w * (-1.0 / (GROUP * THR));
				baseNet[i].b = baseNet[i].b + grad[0][i].b * (-1.0 / (GROUP * THR));
			}
			for (int t = 0; t < THR; t++) {
				Cost += cost[t] / GROUP;
			}
		}
		Save(fg);
		fg ^= 1;
		freopen("diary.out", "a", stdout);
		printf("%lf\n", Cost / (T / GROUP));
		fclose(stdout);
		freopen("/dev/tty", "w", stdout);
		printf("complete turn: %d\n", _i+1);
	}
}
signed main() {
	srand(time(NULL));
	init();
	clock_t st = clock(), en;
	ANN();
	en = clock();
	freopen("diary.out", "a", stdout);
	printf("Learning time: %lf s\n", 1.0 * (en - st) / CLOCKS_PER_SEC);
	fclose(stdout);
	return 0;
}

最后还有一份代码ANN_Check.cpp，用于测试学习效果的，用于检验当前网络的测试数据的正确性

#include <bits/stdc++.h>
#define db double
#define ll long long
#define vi vector<int>
#define vii vector<vi >
#define vd vector<db>
#define vdd vector<vd >
#define pii pair<int, int>
#define pdd pair<db, db>
#define vpd vector<pdd >
#define vipd vector<vpd >
#define vp vector<pii >
#define vip vector<vp >
#define mkp make_pair
#define pb push_back
using namespace std;
const int INF = 0x3f3f3f3f;
const int T = 10000; // Number of Total training Data
const int L = 4; // Number of Layers (contains Input layer and Output layer)
const int IN = 784; // Number of Nodes in Layer 1 (Input Layer)
const int OUT = 10; // Number of Nodes in Layer L-1 (Output Layer)
const int N[L] = {IN, 16, 16, OUT}; // Number of Nodes in each Layer
//vd N(L); 
db image[T][IN]; // Image Data
int ans[T]; // Label of Image Data (Answer)
struct mat{ // Matrix Data Struct
	int n, m; // Size of Matrix : n * m
	vdd M;
	mat() {}
	mat(int n, int m, int num = 0) : n(n), m(m) { M = vdd(n, vd(m, num)); }
	mat operator * (const mat &y) const & { // multiply of Matrix
		assert(m == y.n);
		mat z(n, y.m);
		for (int i = 0; i < n; i++)
			for (int j = 0; j < y.m; j++)
				for (int k = 0; k < m; k++)
					z.M[i][j] += M[i][k] * y.M[k][j];
		return z;
	}
	mat operator + (const mat &y) const & { // addition of Matrix
		assert(n == y.n && m == y.m);
		mat z(n, m);
		for (int i = 0; i < n; i++)
			for (int j = 0; j < m; j++)
				z.M[i][j] = M[i][j] + y.M[i][j];
		return z;
	}
	mat operator * (const double &y) const & { // multiply Matrix and Const
		mat z(n, m);
		for (int i = 0; i < n; i++)
			for (int j = 0; j < m; j++)
				z.M[i][j] = M[i][j] * y;
		return z;
	}
	mat dot(mat &x, mat &y) { // dot multiplay of Matrix
		assert(x.n == y.n && x.m == y.m);
		int n = x.n, m = x.m;
		mat z(n, m);
		for (int i = 0; i < n; i++)
			for (int j = 0; j < m; j++)
				z.M[i][j] = x.M[i][j] * y.M[i][j];
		return z;
	}
	mat operator ~ () const & { // transpose the Matrix
		mat z(m, n);
		for (int i = 0; i < m; i++)
			for (int j = 0; j < n; j++)
				z.M[i][j] = M[j][i];
		return z;
	}
	void print() { // print the Matrix
		for (int i = 0; i < n; i++) {
			for (int j = 0; j < m; j++) {
				printf("%.2lf ", M[i][j]);
			}
			putchar('\n');
		}
		putchar('\n');
	}
}MAT;
struct layer { // Layer of the Network
	mat a, w, b, z;
	int id;
	layer() {}
	layer(int id) : id(id) {
		a = mat(N[id], 1);
		if (id) {
			w = mat(N[id], N[id-1]);
			b = mat(N[id], 1);
		}
	}
}baseNet[L]; // basic network
db getrand() { return 1.0 * rand() / RAND_MAX; }
void init() { // initialize Training Data
	freopen("test.in", "r", stdin);
	for (int i = 0; i < T; i++) {
		for (int j = 0; j < IN; j++) {
			scanf("%lf", &image[i][j]);
			image[i][j] /= 255;
		}
	}
	fclose(stdin);
	freopen("test.out", "r", stdin);
	for (int i = 0; i < T; i++) scanf("%d", &ans[i]);
	fclose(stdin);
	printf("Reading complete!\n");
	// image Input TEST
	//for (int i = 0; i < 784; i++) {
	//	printf("%d ", (int)(image[0][i] * 255));
	//	if ((i+1) % 28 == 0) {
	//		putchar('\n');
	//	}
	//}
}
mat f(mat &x) { // activate function (sigmoid)
	mat z(x.n, x.m);
	for (int i = 0; i < x.n; i++) {
		for (int j = 0; j < x.m; j++) {
			db t = x.M[i][j];
			z.M[i][j] = 1.0 / (1 + exp(-t));
		}
	}
	return z;
}
mat _f(mat &x) { // Derivative of activate function 
	mat z(x.n, x.m);
	for (int i = 0; i < x.n; i++) {
		for (int j = 0; j < x.m; j++) {
			db t = x.M[i][j];
			z.M[i][j] = 1.0 / (exp(t) + exp(-t) + 2);
		}
	}
	return z;
}
// Id of Checking Data
int CK(int id) { // return Output
	layer net[L];
	for (int i = 0; i < L; i++) net[i] = baseNet[i];
	// initialize Input & Desired Data
	for (int i = 0; i < IN; i++) net[0].a.M[i][0] = image[id][i];
	// Forward
	for (int l = 1; l < L; l++) {
		net[l].z = net[l].w * net[l-1].a + net[l].b;
		net[l].a = f(net[l].z);
	}
	double mx = 0;
	int out;
	for (int i = 0; i < OUT; i++) {
		if (net[L-1].a.M[i][0] > mx) {
			mx = net[L-1].a.M[i][0];
			out = i;
		}
	}
	return out;
}
void ANN() { // Artificial Neural Network
	// initialize the struct of Network
	for (int i = 0; i < L; i++) baseNet[i] = layer(i);
	if (freopen("Result.in", "r", stdin) == NULL) { // initialize w and b randomly
		freopen("/dev/tty", "w", stdout);
		printf("Randomly initialization\n");
		for (int l = 1; l < L; l++) {
			for (int i = 0; i < N[l]; i++) {
				for (int j = 0; j < N[l-1]; j++)
					baseNet[l].w.M[i][j] = getrand() * 10 - 5;
				baseNet[l].b.M[i][0] = getrand() * 40 - 20;
			}
		}
	} else { // Using last Learning Data
		freopen("/dev/tty", "w", stdout);
		printf("Get Result.in\n");
		int rL;
		scanf("%d", &rL);
		assert(L == rL);
		vi rN(L);
		for (int i = 0; i < L; i++) {
			scanf("%d", &rN[i]);
			assert(rN[i] == N[i]);
		}
		for (int l = 1; l < L; l++) {
			for (int i = 0; i < N[l]; i++)
				for (int j = 0; j < N[l-1]; j++)
					scanf("%lf", &baseNet[l].w.M[i][j]);
			for (int i = 0; i < N[l]; i++)
				scanf("%lf", &baseNet[l].b.M[i][0]);
		}
		fclose(stdin);
	}
	int yes = 0;
	vi perm(T);
	for (int i = 0; i < T; i++) perm[i] = i;
	random_shuffle(perm.begin(), perm.end());
	for (int i = 0; i < T; i++) {
		if (CK(i) == ans[i]) yes++;
	}
	freopen("/dev/tty", "w", stdout);
	printf("%lf", 1.0 * yes / T);
}
signed main() {
	srand(time(NULL));
	init();
	ANN();
	return 0;
}

（我的代码折叠器坏了，只能先这样了😢）

学习效果

经过多线程计算，5h后第一组数据基本收敛了，最后的正确率到达 81%（yysy第一次能到这个正确的，我觉得还行了），而别人做的可以到达 90% 以上，最近几天还在计算中，希望能有所提高。

总算，经过不断修改（线程计算上改了半天，对收敛没有任何效果），最后发现原因在于初始值的设定上，最后将初始值设定在 $[-1,1]$ 上，可以使得最后的精确率达到 94%（只用计算不到20分钟，200次即可达到这个精确率），总算是验证了我的写法是没有问题了！🎉