曲线及其长度 第一型曲线积分

第六周把重积分讲完了进入下一章（好像没讲广义重积分），进入学习曲线积分，先是定义较多，对定义的理解很重要，上一章的习题课还要补（）。

（分段）光滑曲线及其长度

定义1（简单曲线）

设 $C\subset \mathbb R^n$，$\alpha:[a, b]\rightarrow C$，满足：

1. $\alpha$ 为双射。

2. $\alpha, \alpha^{-1}$ 连续。

则称 $C$ 为 $\mathbb R^n$ 中的简单曲线，称 $\alpha$ 为 $C$ 的参数方程。

设 $P\in C,\ P=\alpha(t_0)$，则称 $t_0$ 为 $P$ 的参数或坐标。

若 $t_0\in\{a, b\}$，则 $P$ 为端点，若 $a < t_0 < b$，则 $P$ 为内点，由内点构成的集合称为内部。

---

不难发现，要求双射，则 $C$ 一定不能有交点，要求连续，则 $C$ 不能有间断点。

定义2（光滑曲线）

设 $C\subset \mathbb R^n$，$\alpha:[a, b]\rightarrow C$，满足

1. $\alpha$ 为双射，$\alpha, \alpha^{-1}$ 连续（简单曲线）。

2. $\alpha \in C^k,\ (1\leqslant k\leqslant +\infty)$（光滑性）。

3. $\alpha'(t)\neq \vec{0},\ \forall t\in[a, b]$（正则性）。

则称 $C$ 为 $C^k - \text{光滑的正则曲线}$（也称光滑曲线），称 $\alpha$ 为 $C$ 的参数方程。

---

光滑曲线的正则性能够保证切线存在（也就是说折线不是光滑曲线）。

令 $\alpha$ 为光滑曲线 $C$ 的参数方程，$\forall t\in[a,b ]$，则 $\alpha(t)$ 处的切向量为 $\alpha'(t)$，单位切向量为 $\tau=\dfrac{\alpha'(t)}{|\alpha'(t)|}$，$\alpha(t_0)$ 处的切线为：

$$l = \{\alpha(t_0) + \alpha'(t_0)(t-t_0):t\in\mathbb R\}$$

比如：$\alpha(t) = (t^2, t^3)$，$t\in[-1,1]$，$C=\alpha([-1, 1])$，图像如下：

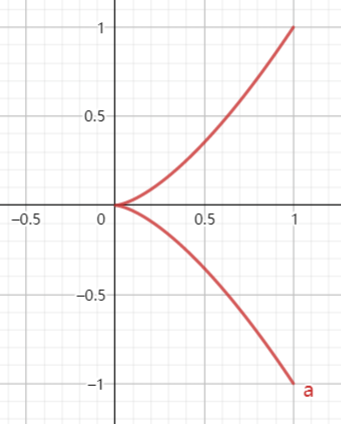
$\alpha'(0) = 0$，$C$ 在 $(0, 0)$ 处并不光滑。

定义3（曲线长度&弧长）

设 $C\subset \mathbb R^n$ 为光滑曲线，$\alpha:[a, b]\rightarrow C$ 为 $C$ 的参数方程，设 $\pi:a=t_0 < t_1 < \cdots < t_N = b$ 为 $[a, b]$ 的分划，记

$$S =\sum_{i=1}^N|\mathop{\alpha(t_{i-1})\alpha(t_i)}\limits^{--------\rightarrow}|$$

如果 $\lim\limits_{\Delta\pi\rightarrow 0}S$ 存在，记 $L(C) = \lim\limits_{\Delta\pi\rightarrow 0}S$，并称之为曲线 $C$ 的长度（弧长）。

其中 $\mathop{AB}\limits^{--\rightarrow}$ 表示：以 $A$ 为起点，$B$ 为终点的向量（不用向量减法，因为可以不用建系）。

---

形象理解这个定义，就是把曲线分成很多小段，然后求和，得到整个弧长。

$\KaTeX$ 中实在没有找到长箭头，只能用 $\mathop{\ }\limits^{--\rightarrow}$ 代替了~~

定理4（弧长的积分形式）

设 $C\subset \mathbb R^n$ 为光滑曲线，$\alpha:[a, b]\rightarrow C$ 为 $C$ 的参数方程，则

$$L(C) = \int_{a}^b|\alpha'(t)|\,dt$$

---

思路： 对 $\int_a^b|\alpha'(t)|\,dt$ 展开成 $Riemann\text{和}$ 的形式，再对两式进行估计即可。

证明：

由于当 $\Delta\pi\rightarrow 0$ 时，$\int_a^b|\alpha'(t)|\,dt = \sum\limits_{i=1}^N|\alpha'(t_{i-1})|(t_i-t_{i-1})$

$$\begin{aligned} &\left|\sum_{i=1}^N|\mathop{\alpha(t_{i-1})\alpha(t_i)}\limits^{--------\rightarrow}|-\sum_{i=1}^N|\alpha'(t_{i-1})|(t_i-t_{i-1})\right|\\ \text{（使用两次三角不等式）}\leqslant&\sum_{i=1}^N|\mathop{\alpha(t_{i-1})\alpha(t_i)}\limits^{--------\rightarrow}-\alpha'(t_{i-1})(t_i-t_{i-1})|\\ =&\sum_{i=1}^N\left|\int_{t_{i-1}}^{t_i}\alpha'(t)\,dt-\int_{t_{i-1}}^{t_i}\alpha'(t_{i-1})\,dt\right|\\ \leqslant&\sum_{i=1}^N\int_{t_{i-1}}^{t_i}|\alpha'(t)-\alpha'(t_{i-1})|\,dt\\ \text{令}\omega(\Delta\pi)=\sup_{|t-s|\leqslant\Delta\pi}|\alpha'(t)-&\alpha'(s)|\text{，由}\alpha'\text{的一致连续性知}\omega(\Delta\pi)\rightarrow 0\\ \text{原式}\leqslant&(b-a)\cdot\omega(\Delta\pi)\rightarrow 0 \end{aligned}$$

QED

于是我们就可以愉快地求圆的周长了（

例一（圆的周长）

$C = \{(x, y):x^2+y^2=1, y\geqslant 0\}$，计算 $L(C)$。

解： $C$ 的参数方程为：$\alpha(\theta)=(\cos\theta,\sin\theta),\ \theta\in[0,\pi]$，则

$$L(C) = \int_0^{\pi}1\,d\theta=\pi$$

例二（二维函数图像的长度）

$f\in C^1([a,b]),\ C = \text{graph } f=\{(x, f(x)): x\in[a, b]\}$，求 $L(C)$。

解： $C$ 的参数方程为：$\alpha(x) = (x, f(x)),\ x\in[a, b]$，则

$$L(C) = \int_a^b\sqrt{1+|f'(x)|^2}\,dx$$

定义5（分段光滑曲线）

设 $C\subset \mathbb R^n$，$\alpha:[a, b]\rightarrow C$ 连续，设 $a=a_0 < a_1 < \cdots < a_N = b$，

记： $\alpha_i = \alpha\bigg|_{[a_{i-1}, a_i]},\ C_i = \alpha_i([a_{i-1}, a_i])$，若满足：

1. $C_i$ 为光滑曲线，$\alpha_i$ 为 $C_i$ 的参数方程（$i=1\sim N$）。

2. $C_i$ 内部互不相交。

则称 $C$ 为分段光滑曲线，$\alpha$ 为 $C$ 的参数方程，并记 $C=C_1+C_2+\cdots+C_N$。

并定义 $\alpha'(t) = \alpha_i'(t),\ t\in(a_{i-1}, a_i)$，对于 $\alpha'(a_i)$ 上的函数值可以任取，由于 $\alpha'$ 只在有限多个点处间断，所以

$$L(C_i) = \int_{a_{i-1}}^{a_i}|\alpha_i'|\,dt=\int_{a_{i-1}}^{a_i}|\alpha'|\,dt$$

---

由于折线可以分解成很多段光滑的曲线，所以折线就是分段光滑曲线，从而折线上的积分我们接下来也可以求解了。

定义6（分段光滑曲线的长度）

设 $C\subset \mathbb R^n$，$C$ 为分段光滑积分，可以分解为：$C=C_1+C_2+\cdots+C_N$，记

$$L(C) = \sum_{i=1}^NL(C_i)$$

定理7（分段光滑曲线长度的积分形式）

设 $C\subset \mathbb R^n$ 为分段光滑曲线，$\alpha:[a, b]\rightarrow C$ 为 $C$ 的参数方程，则

$$L(C) = \int_a^b|\alpha'|\,dt$$

---

利用一维积分的可加性即可证明。

第一型曲线积分

该定义是从物理问题引出的，也称 $f$ 沿着曲线积分。

定义1（第一型曲线积分）

设 $C\subset \mathbb R^n$ 为光滑曲线，$\alpha:[a, b]\rightarrow C$ 为 $C$ 的参数方程。

$f:C\rightarrow \mathbb R$，设 $\pi:a=t_0 < t_1 < \cdots < t_N = b$ 为 $[a, b]$ 的分划，考虑和式

$$S = \sum\limits_{i=1}^Nf(\xi_i)L(C_i)$$

其中 $C_i = \alpha([t_{i-1}, t_i]),\ \xi_i\in C_i$

如果 $\exists I \in\mathbb R$，满足 $\forall \varepsilon > 0, \exists\delta > 0$，使当 $\Delta\pi\leqslant \delta$ 时，$|S-I|\leqslant \varepsilon,\ (\forall \xi_i\in C_i)$，则称 $\lim\limits_{\Delta\pi\rightarrow 0}S$ 存在，并定义 $\lim\limits_{\Delta\pi\rightarrow 0}S = I$，如果 $\lim\limits_{\Delta\pi\rightarrow 0}S$ 存在，记

$$\int_{C}f\,ds = \lim_{\Delta\pi\rightarrow 0}S$$

称为 $f$ 沿曲线 $C$ 的积分，也可以记为 $\int_Cf(x)\,ds$，这里的 $x$ 是 $n$ 维向量。

---

注： $ds$ 在这里是形式的记号，表示单位长度，如果曲线看做钢丝，将 $f(x)$ 看做钢丝密度（单位长度上的质量），那么 $\int_{C}f\,ds$ 就是整个钢丝的质量。

定理2（第一型曲线积分计算方法）

设 $C\subset\mathbb R^n$ 为光滑曲线，$\alpha:[a,b]\rightarrow C$ 为 $C$ 的参数方程，设 $f:C\rightarrow \mathbb R$ 连续，则

$$\int_Cf\,ds=\int_a^bf(\alpha(t))|\alpha'(t)|\,dt$$

---

思路： 和 定理4（弧长的积分形式） 证明方法类似，都是拆开以后，做差用三角不等式估计。

证明：

$$\begin{aligned} &\left|S - \int_a^bf(\alpha(t))|\alpha'(t)|\,dt\right|\\ =&\left|\sum_{i=1}^Nf(\alpha(t_i))\int_{t_{i-1}}^{t_i}|\alpha'(t)|\,dt-\sum_{i=1}^N\int_{t_{i-1}}^{t_i}f(\alpha(t))|\alpha'(t)|\,dt\right|\\ \leqslant&\sum_{i=1}^N\left|\int_{t_{i-1}}^{t_i}(f(\alpha(t_i))-f(\alpha(t)))|\alpha'(t)|\,dt\right|\\ \leqslant&\sum_{i=1}^N\int_{t_{i-1}}^{t_i}|f(\alpha(t_i))-f(\alpha(t))|\cdot|\alpha'(t)|\,dt\\ \leqslant& L(C)\cdot\omega(\Delta\pi)\rightarrow 0 \end{aligned}$$

其中 $\displaystyle \omega(\Delta\pi) = \sup_{|t-s|\leqslant\Delta\pi}|f(\alpha(t))-f(\alpha(s))|$，当 $\Delta\pi\rightarrow 0$ 时， $\omega(\Delta\pi)\rightarrow 0$。

QED

例一（二维函数图像上的积分）

函数图像的定义和 例二 - 二维函数图像的长度 一致，设 $g:C\rightarrow \mathbb R$ 连续，则

$$\int_Cg\,ds = \int_a^bg(x, f(x))\sqrt{1+|f'(x)|^2}\,dx$$

不难发现，令 $g=1$，则 $\displaystyle \int_C\,ds = L(C)$。

由于第一型曲线积分 $\iff$ 一元函数的积分，所以它有积分的众多性质，比如

定理3（保号性和线性性）

设 $C\subset \mathbb R^n$ 为光滑曲线，$f, g:C\rightarrow \mathbb R$ 连续。

1. 如果 $f\geqslant 0$，则 $\int_Cf\,ds\geqslant 0$，“$=$” 成立当且仅当 $f\equiv 0$。

2. 如果 $k, l\in \mathbb R$，则 $\int_C(kf+lg)\,ds= k\int_Cf\,ds+l\int_Cg\,ds$。

---

对于分段光滑曲线同样可以定义 $f$ 在其上的积分。

定义4（分段曲线上的积分）

设 $C$ 为分段光滑曲线，$C=C_1+C_2+\cdots+C_N$，设 $f:C\rightarrow \mathbb R$ 连续，记

$$\int_Cf\,ds = \sum_{i=1}^N\int_{C_i}f\,ds$$

---

由于 $f\circ\alpha$ 在 $[a, b]$ 上只有有限个间断点，所以

$$\int_Cf\,ds = \int_a^bf(\alpha(t))|\alpha'(t)|\,dt$$

定理5（三种变换）

设 $Q\in\mathbb R^{n\times n}$ 为正交阵，$r>0, v\in\mathbb R^n$，记 $T:\mathbb R^n\rightarrow \mathbb R^n$，$Tx=rQx+v$，则

$$\int_{T(C)}f(x)\,ds = r\int_{C}f(Tx)\,ds$$

---

$Q$ 代表正交变换（旋转和对称）；

$r$ 代表伸缩变换（ 注： 是整体伸缩，不能对某一维伸缩）；

$v$ 代表平移变换。

思路： 先写出 $T(C)$ 的参数方程 $\beta$，然后对其求解，最后再转换回 $\alpha$，最终回到 $C$ 上。

证明： 设 $C$ 的参数方程为 $\alpha:[a, b]\rightarrow C$，则 $T(C) = \{rQ\alpha(t)+v:t\in[a, b]\}$，

令 $\beta(t)=rQ\alpha(t)+v,\ (t\in[a, b])$，则 $\beta$ 为 $T(C)$ 的参数方程，于是

$$\begin{aligned} \int_{T(C)}f(x)\,ds =& \int_a^bf(\beta(t))|\beta'(t)|\,dt\\ =&\ r\int_a^bf(rQ\alpha(t)+v)|\alpha'(t)|\,dt\\ \xlongequal{\text{逆向使用定理2}}&\ r\int_Cf(rQx+v)\,ds\\ =&\ r\int_Cf(T(x))\,ds \end{aligned}$$

QED

例一

$\partial B_r(x_0)=\{x\in\mathbb R^2:|x-x_0|=r\}$，则

$$\begin{aligned} &\int_{\partial B_r(x_0)}f(y)\,ds\\ \xlongequal{y=x+x_0}&\ \int_{\partial B_r}f(x+x_0)\,ds\\ \xlongequal{x=rz}&\ r\int_{\partial B_1}f(rz+x_0)\,ds \end{aligned}$$

例二

$C = \{(x, y, z)\in\mathbb R^3:x^2+y^2+z^2=a^2, x+y+z=0\}$，计算下列积分：

1. $\int_Cx^2\,ds$

2. $\int_Cxy\,ds$

3. $\int_Cxyz\,ds$

解：

$$\begin{aligned} &1. \begin{aligned}\displaystyle \int_Cx^2\,ds=\int_Cy^2\,ds=\int_Cz^2\,ds=\frac{1}{3}\int_C(x^2+y^2+z^2)\,ds=\frac{a^2}{3}L(C)=\frac{2\pi a^3}{3}\end{aligned}\\ &2. \begin{aligned}\displaystyle \int_Cxy\,ds=\int_Cxz\,ds=\int_Cyz\,ds=\frac{1}{6}\int_C((x+y+z)^2-x^2-y^2-z^2)\,ds=-\frac{a^2}{6}L(C)=-\frac{\pi a^3}{3}\end{aligned}\\ &3. \begin{aligned}\int_Cxyz\,ds\xlongequal[\begin{aligned}x&=-x\\y&=-y\\z&=-z\end{aligned}]{\text{做对称变换}}-\int_Cxyz\,ds\Rightarrow \int_Cxyz\,ds=0\end{aligned}\\ \end{aligned}$$

我们现在再回去看多元积分变量代换中的极坐标变换 note4 - 对坐标变换的思考，不难发现，这部分其实就是

$$\int_0^{2\pi}f(r\cos\theta, r\sin\theta)r\,d\theta = \int_{\partial B_r} f \,ds$$

所以圆盘上的积分也可以写做：

$$\int_{B_R(x_0)}f\,dx = \int_0^R\left\{\int_{\partial B_r(x_0)}f\,ds\right\}\,dr$$

结合这张图就更容易理解原因了。