因为一阶微分方程的类型颇多,解法也多种多样,故在国庆间,将前三周所讲内容做一点总结,以便复习时参考,下面都只给出结论,并没有给出推导过程。
线性方程
dxdy+P(x)y=Q(x)
解法: 令 y=u(x)exp(−∫P(x)dx),再将其带回,得
u′(x)exp(−∫P(x)dx)=Q(x)u(x)=∫(Q(x)exp(∫P(x)dx))dx
从而 y=(∫(Q(x)exp(∫P(x)dx))dx)exp(−∫P(x)dx)
Bernoulli 方程
dxdy+P(x)y=Q(x)yn(n∈Z,n=0,1)
解法:
⇒ 令⇒ dxdy+P(x)y=Q(x)yndxdyy−n+P(x)y1−n=Q(x)z=y1−n, 则 dxdz=dxdy(1−n)y−ndxdz+(1−n)P(x)z=(1−n)Q(x)
转换为 线性方程 。
变量可分离方程
dxdy=f(x)g(y)
解法:
⇒ ⇒ dxdy=f(x)g(y)g(y)1dy=f(x)dx∫g(y)1dy=∫f(x)dx
齐次方程
定义
设 n 元函数 f(x1,x2,…,xn),若 f(x1,x2,…,xn) 满足
f(tx1,tx2,…,txn)=tmf(x1,x2,…,xn)
则称 f(x1,x2,…,xn) 为 m 次齐次方程。
且有 Euler定理 j=1∑n∂xj∂fxj=mf。
解法
令⇒ 求解 dxdy=F(xy)z=xy, 则 z+xdxdz=dxdyz+xdxdz=F(z)
转换为 变量可分离方程 。
可转换为其次方程的方程
dxdy=f(a2x+b2y+c2a1x+b1y+c1)
解法:
-
当 c1=c2=0 时,直接回到 齐次方程。
-
当 c12+c22=0 时,
- ∣∣∣∣∣a1a2b1b2∣∣∣∣∣=0,则方程 {a1x+b1y+c1=0a2x+b2y+c2=0 有解,
设该方程的解为 {x=αy=β,做变量替换,令 {x=x′+αy=y′+β 则
原方程⟺dx′dy′=f(a2x′+b2y′a1x′+b1y′)⟺dxdy=f(a2x+b2ya1x+b1y)
- 转换为 齐次方程。
- ∣∣∣∣∣a1a2b1b2∣∣∣∣∣=0,则 ∃λ,使得 {a1=λa2b1=λb2,设 z=a1x+b1y,则 dxdz=a1+b1dxdy。
原方程⟺dxdz=a1+b1f(λz+cz+c)
全微分方程
定义
⟺⟺M(x,y)dx+N(x,y)dy=0 为全微分方程存在二元可微函数 f,使得df(x,y)=∂x∂fdx+∂y∂fdy=M(x,y)dx+N(x,y)dy∂y∂M(x,y)=∂x∂N(x,y)
解法(偏微分法)
求解全微分方程 M(x,y)dx+N(x,y)dy=0 的解。
若能找到 df=M(x,y)dx+N(x,y)dy)=0,则原方程的解为 f=C。
令 f=∫M(x,y)dx+g(y),带回原式中,得
⇒ ∂y∂f=∂y∂(∫M(x,y)dx)+g′(y)=N(x,y)g(y)=∫(N(x,y)−∂y∂(∫M(x,y)dx))dy
将 g(y) 带回到 f 中即可。
凑微分
记住几个常用的:
ydx+xdyy2ydx−xdyx2xdy−ydxxyydx−xdyx2+y2ydx−xdyx2−y2ydx−xdyex(dy+ydx)=d(xy)=d(yx)=d(xy)=d(log∣∣∣∣∣yx∣∣∣∣∣)=d(arctan(yx))=21d(log∣∣∣∣∣x+yx−y∣∣∣∣∣)=d(yex)
不难发现,这几个常微分大都和 (ydx−xdy) 有关,所以看到这一项先提出来,尝试凑微分。
积分因子
定义
若 M(x,y)dx+N(x,y)dy=0 不是全微分方程,但乘上可微函数 μ(x,y) 后变为全微分,那么称 μ 为该方程的积分因子。
解法
由于能力匮乏,只能求解 μ 和单变量有关的通解。
-
若 MNx−My 只和 y 有关,则 μ(y)=exp(∫MNx−Mydy)。
-
若 NMy−Nx 只和 x 有关,则 μ(x)=exp(∫NMy−Nxdx)。
积分因子结合
若 M1(x,y)dx+N1(x,y)dy+M2(x,y)dx+N2(x,y)dy=0 对于积分因子 μ1(x,y),μ2(x,y) 分别是全微分方程,也就是说,存在 F1(x,y),F2(x,y) 使得
dF1=μ1M1dx+μ1N1dy=0dF2=μ2M2dx+μ2N2dy=0
那么方程 M1(x,y)dx+N1(x,y)dy+M2(x,y)dx+N2(x,y)dy=0 有公共的积分因子 μ,当且仅当,存在 G1(x),G2(x),使得
μ1(x,y)G1(F1(x,y))=μ2(x,y)G2(F2(x,y))
则公共因子 μ=μ1(x,y)G1(F1(x,y))。
变量替换
形式一
求解
dxdy=f(ax+by+c)
令 z=ax+by+c,则 dxdz=a+bdxdy。
原方程⟺dxdz=a+bf(z)
转换为 变量可分离方程。
形式二
求解
yf(xy)dx+xg(xy)dy=0
令 z=xy,则 dxdz=y+xdxdy⇒dz=ydx+xdy=xzdx+xdy
原方程⟺xzf(z)dx+g(z)(dz−xzdx)=0⟺g(z)dz+xdx(f(z)−g(z))z=0
转换为 变量可分离方程。
Riccati 方程
形如
dxdy=P(x)y2+Q(x)y+R(x)
- R(x)=0 时,利用特解 φ(x),令 y=z+φ(x)。
代入原方程中:
dxdy=dxdz+dxdφdxdz=P(x)(z2+2zφ(x)+φ2(x))+Q(x)(z+φ(x))+R(x)=(P(x)φ2(x)+Q(x)φ(x)+R(x)−dxdφ)+P(x)z2+2P(x)φ(x)z+Q(x)z=(2P(x)φ(x)+Q(x))z+P(x)z2
转化为 Bernoulli方程。
- 形如
dxdy+ay2=xly+x2b
解法:
⇒ 令⇒ dxdy+ay2=xly+x2bdxdyx2+ax2y2=lxy+bz=xy, 则 dxdz=y+xdxdy⇒xdxdz=z+x2dxdydxdzx−z+az2=lz+b
转换为 变量可分离方程。
- 形如
dxdy+ay2=bxm
当 m=0 或 −2 或 2k+1−4k 或 2k−1−4k(k∈Z⩾1) 时,有解。
当 m=−2 时,使用变量替换 z=xy 即可。
一阶隐式微分方程
上面所提及的解法都是针对显式微分方程 y′=f(x,y) 的,下面考虑未能解出 y′ 的一阶隐式方程
F(x,y,y′)=0
主要思路:将隐式方程转化为一个或多个显式方程,从而将问题转化为求解显式方程上。
主要方法:参数法,令 y′=dxdy=p 将 p 视为变量,利用两边同时求导将 p 解出,从而解出 y。
可以解出x或y的方程
第一种
y=f(x,y′)
解法
令 y′=p,则 y=f(x,p),将该式两边同时对 x 求导,则
p=y′=∂x∂f(x,p)+∂p∂f(x,p)⋅dxdp
利用一阶显式方程解法,解出 p=φ(x),代入 y=f(x,p) 中,得
y=f(x,φ(x))
注:如果有多个解,则都要代入一遍。
第二种
x=f(y,y′)
解法
令 y′=p,则 x=f(y,p), dxdp=dxdy⋅dydp=pdydp,将该式两边同时对 x 求导,则
11=∂y∂f(y,p)⋅dxdy+∂p∂f(y,p)⋅dxdp=p(∂y∂f(y,p)+∂p∂f(y,p)⋅dydp)
利用一阶显式方程解法,解出 p=φ(y),代入 x=f(y,p) 中,得
x=f(y,φ(y))
同样的,如果有多个解,则都要代入一遍。
不显含x或y的方程
第一种
F(y,y′)=0
解法
令 p=y′,则 F(y,p)=0,可以视为 yOp 上的曲线,设其有如下的参数表示法:
{y=ψ(t)p=h(t)⇒{dy=ψ′(t)dtdy=h(t)dx
则有
dx=h(t)ψ′(t)dt⇒x=∫h(t)ψ′(t)dt
故有参数表示法
⎩⎪⎨⎪⎧x=∫h(t)ψ′(t)dty=ψ(t)
第二种
F(x,y′)=0
解法
令 p=y′,则 F(x,p)=0,可以视为 xOp 上的曲线,设其有如下的参数表示法:
{x=φ(t)p=h(t)⇒{dx=φ′(t)dtdy=h(t)dx
则有
dy=h(t)φ′(t)dt⇒y=∫h(t)φ′(t)dt
故有参数表示法
⎩⎪⎨⎪⎧x=φ(t)y=∫h(t)φ′(t)dt
近似解法
对于初值问题:⎩⎪⎨⎪⎧dxdy=f(x,y)y(x0)=y0
有如下两种函数近似解法,和两种数值近似解法。
逐次迭代法(Picard iteration methods)
利用初值问题的积分形式 y=y0+∫x0xf(ψ,y(ψ))dψ 递归生成Picard序列。
在满足Lipschitz条件的前提下,Picard序列收敛。
⎩⎪⎨⎪⎧φ0(x)=y0φn(x)=y0+∫x0xf(ξ,φn−1(ξ))dξ
令真实解为 ψ(x)=y0+∫x0xf(ξ,ψ(ξ))dξ。
∣ψ(x)−φ0(x)∣∣ψ(x)−φ1(x)∣=∣∣∣∣∣∫x0xf(ξ,ψ(ξ))dξ∣∣∣∣∣⩽∫x0x∣f(ξ,ψ(ξ))∣dξ=∣∣∣∣∣∫x0xf(ξ,ψ(ξ))−f(ξ,φ0(ξ))∣∣∣∣∣dξ⩽∫x0x∣f(ξ,ψ(ξ))−f(ξ,φ0(ξ))∣⩽L∫x0x∣ψ(x)−φ0(x)∣dξ⩽LM∫x0x(ξ−x0)dξ⩽2!ML(x−x0)2⩽2!MLh2
其中 L 为 Lipschitz 常数,满足 ∣f(x,y1)−f(x,y2)⩽L∣y1−y2∣,对任意的 (x,y1),(x,y2)∈R 都成立,R 为初始值邻域。M=(x,y)∈Rmax∣f(x,y)∣,h=min(a,Mb)。
由数学归纳法,得
∣ψ(x)−φn(x)∣⩽n!MLn−1hn
这样证明了 Picard 序列是收敛的,而且对其进行了误差估计。
Picard 序列的困难就在于,它需要反复积分,迭代多次后,计算十分复杂。
Taylor 级数法
直接尝试去计算 y(x) 在 x0 处的泰勒展开式
y(x)=n=0∑∞n!y(n)(x0)(x−x0)n
能这样展开求的理论基础,书上(没有证明),老师给了(柯西定理),应该就是 知乎 - 常微分方程学习笔记(8) 中 7.1 的柯西定理(我tcl)。
然后逐项求出:
y(x0)y′(x0)y′′(x0)y′′′(x0)y′′′′(x0)=y0=f(x0,y0)=dxdf(x,y)∣∣∣∣∣x=x0=f(x0,y0)=dxdf(x,y)=(fx(x,y)+fy(x,y)f(x,y))∣∣∣∣∣x=x0=fx(x0,y0)+fy(x0,y0)f(x0,y0)=dxd(fx(x,y)+fy(x,y)f(x,y))=fxx(x,y)+2fxy(x,y)f(x,y)+fyy(x,y)f2(x,y)+fx(x,y)fy(x,y)+fy2(x,y)f(x,y)∣∣∣∣∣x=x0=fxx(x0,y0)+2fxy(x0,y0)f(x0,y0)+fyy(x0,y0)f2(x0,y0)+fx(x0,y0)fy(x0,y0)+fy2(x0,y0)f(x0,y0)
然后再带回到 y(x) 的 Taylor 展开式中即可。
该方法的缺点在于,y 的高阶导数过于难求,所以有了下面的待定系数法。
待定系数法(幂级数法)
由于 y 的高阶导数很难求,所以考虑将其设成常数 an,令
y则 y′=n=0∑∞n!y(n)(x0)(x−x0)n=n=0∑∞an(x−x0)n=n=0∑∞nan(x−x0)n−1
代入到 y′=f(x,y) 中,得
n=0∑∞nan(x−x0)n−1=f(x,n=0∑∞an(x−x0)n)
如果要求解多项式展开中某一项的系数,可以使用 多项式定理。
再通过对比同次幂系数得出 an。这样就避免了直接求解 y 的导数。
下面两个方法都是数值解法,也就是通过近似的方法求一些离散点 x0,x1,⋯,xn 上的函数值,而不求函数。(最后可以通过函数拟合的方法求近似解)
两种算法都会使用 Python 进行实现。
Euler 折线法
为了计算出初始值问题在区间 [x0,x0+b] 上离散点处的近似值,
我们将区间进行 n 等分,令 h=nb,xk=x0+kh (k=1,2,⋯,n)。
Euler 折线法思路是当 h 很小的时候,(xi,y(xi)) 和 (xi+1,y(xi+1)) 处的斜率近似,即
y′(xi)⇒y(xi+1)⇒y(xi+1)=hy(xi+1)−y(xi)=y(xi)+hy′(xi)=y(xi)+hf(xi,yi)
其实就是利用相邻两点的切线对下一个点的位置进行估计(思虑感觉和牛顿迭代法差不多),即
y0y1y2yn=初始值=y0+hf(x0,y0)=y1+hf(x1,y1) ⋮=yn−1+hf(xn−1,yn−1)
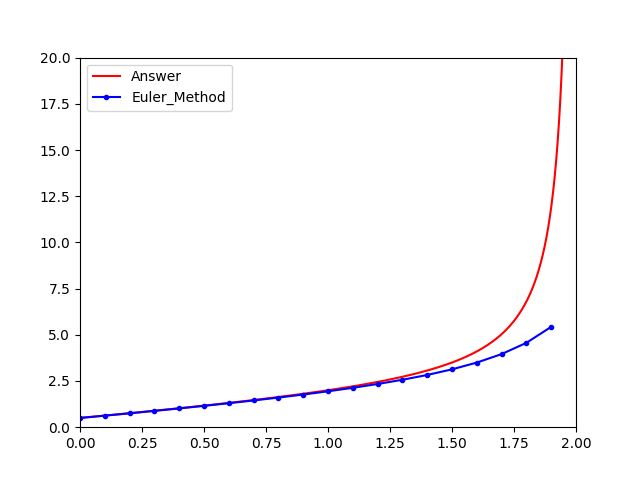
Euler折线法 只是用了 (xi,yi) 处的斜率,对 xi+1,yi+1) 进行估计,可以看到误差还是会很大的,那么考虑,如果使用两处的斜率会怎样呢?
设 k1=f(xi,yi),k2=f(xi+h,yi+k1h),不难发现 k2 其实就是 Euler折线法 中 (xi+1,yi+1) 处的斜率,那么如果我们将 yi+1 通过 k1,k2 的算术平均值得出来,结果是不是会好看些?也就是
yi+1=yi+h⋅2k1+k2
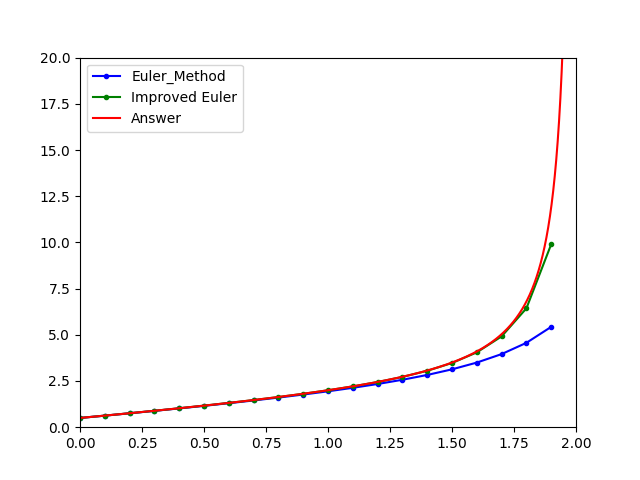
Runge-Kutta
Runge-Kutta 思路是从 优化Euler折线法上得来的,既然说斜率可以通过 k1,k2 平均来优化,那么为什么不是加权平均呢?
于是,就设出加权参数,转化为方程:
⎩⎪⎪⎨⎪⎪⎧yi+1=yi+h(λ1k1+λ2k2)k1=f(x1,y1)k2=f(xi+ph,yi+phk1)⑴⑵⑶
求解方法分为三步:
- 对 k2 在 xi 处做二阶 Taylor展开(知乎 - 多元函数的泰勒展开式)。
k2=f(xi+ph,yi+phk1)=f(xi,yi)+phfx∣∣∣∣∣x=xi+phk1fy∣∣∣∣∣x=xi+O(h2)=f(xi,yi)+ph(fx+y′fy)∣∣∣∣∣x=xi+O(h2)=y′(xi)+phy′′(xi)+O(h2)
- 将 k1,k2 带回到 ⑴ 中。
yi+1=y(xi+1)=yi+h(λ1y′(xi)+λ2y′(xi)+λ2phy′′(xi))+O(h2)=y(xi)+(λ1+λ2)hy′(xi)+λ2ph2y′′(xi)+O(h2)
- 将 y 在 xi 处做二阶 Taylor展开,并代入 xi+1。
yi+1=y(xi+1)=y(xi)+hy′(xi)+2h2y′′(xi)+O(h2)
通过对比系数,可以发现:
⎩⎪⎨⎪⎧λ1+λ2=1λ2p=21
该方程无固定解,而 优化Euler折线法 就是其中的一个特解 ⎩⎪⎨⎪⎧λ1=λ2=21p=1,这也说明了,Euler折线法的精度最高只能做到二阶。
上面举例用的是二阶,如果使用 xi,xi+1 之间更多的离散点值,引入更多的参数,再取一组特解,就可以使精度达到更高阶,这就是 Runge-Kutta 算法的原理。
知乎 - 龙格-库塔(Runge-Kutta)公式 他推导了三阶的,在第一步Taylor展开中也只展开到了第二阶,第三阶实在是复杂,但也看到过程是十分的复杂。
下面给出 四阶经典 Runge-Kutta 公式。
⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧yi+1=yi+6h(k1+2k2+2k3+k4)k1=f(xi,yi)k2=f(xi+2h,yi+2hk1)k3=f(xi+2h,yi+2hk2)k4=f(xi+h,yi+hk3)y0=y(x0)
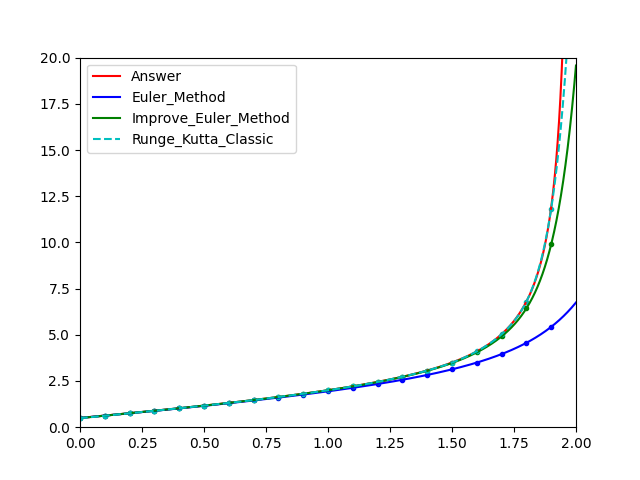
可以看出很明显的区别了。
Python算法&制图代码
上面三张图片都是基于初始值问题
{y′=1+(y−x)2y(0)=0.5
Python 绘图,基于 numpy 和 matplotlib.pyplot 这两个基础包。
import numpy as np
import matplotlib.pyplot as plt
ax = plt.subplot(111)
def Euler_Method():
X = list()
Y = list()
y = y0
for x in np.arange(x0, end, h):
X.append(x)
Y.append(y)
k = f(x, y)
y = y + k * h
ax.plot(X, Y, 'b.')
return np.polyfit(X, Y, 10)
def Euler_Mid_Method():
X = list()
Y = list()
y = y0
for x in np.arange(x0, end, h):
X.append(x)
Y.append(y)
k1 = f(x, y)
k2 = f(x + h, y + k1 * h)
y = y + (k1 + k2) / 2 * h
ax.plot(X, Y, 'g.')
return np.polyfit(X, Y, 12)
def Runge_Kutta_Classic():
X = list()
Y = list()
y = y0
for x in np.arange(x0, end, h):
X.append(x)
Y.append(y)
k1 = f(x, y)
k2 = f(x + h/2, y + h/2 * k1)
k3 = f(x + h/2, y + h/2 * k2)
k4 = f(x + h, y + h * k3)
y = y + h/6 * (k1+2*k2+2*k3+k4)
ax.plot(X, Y, 'c.')
return np.polyfit(X, Y, 12)
x0 = 0
y0 = x0 + 1/(2-x0)
end = 2
h = 0.1
f = lambda x, y: 1 + (y - x)**2
f1 = Euler_Method()
f2 = Euler_Mid_Method()
f3 = Runge_Kutta_Classic()
x = np.arange(0, 2, 0.0001)
y = x + 1 / (2 - x)
y1 = np.polyval(f1, x)
y2 = np.polyval(f2, x)
y3 = np.polyval(f3, x)
ax.axis([0, 2, 0, 20])
ax.plot(x, y, 'r', label = 'Answer')
ax.plot(x, y1, 'b', label = 'Euler_Method')
ax.plot(x, y2, 'g', label = 'Improve_Euler_Method')
ax.plot(x, y3, '--c', label = 'Runge_Kutta_Classic')
plt.legend(loc = 2)
plt.savefig('fig.png')
plt.show()


