TensorFlow - 使用GradientTape和重写fit训练结果不同的原因
该问题是在使用GradientTape训练MNIST数据集时发现的,尝试使用了三种方式进行训练:直接GradientTape训练,调用fit函数训练,重写fit函数后训练. 发现重写GradientTape训练的正确率尽然有96%,而后两者的正确率90%都不到,这引起了我很大的好奇心,于是通过查阅大量文档和阅读TF源代码一步一步排除问题,最终找到问题原因.
训练集使用最简单的MNIST,重写fit函数部分参考:Keyird - 1. 手写数字识别
三种基础模型训练方法
batch大小统一为 ,epoch个数为 ,优化器均采用 keras.optimizers.SGD(lr=0.01)(学习率为0.01),损失函数使用均方误差损失,网络结构如下
dense_network = Sequential([
layers.Flatten(),
layers.Dense(256, activation='relu'),
layers.Dense(128, activation='relu'),
layers.Dense(10)
])
dense_network.build(input_shape=(None, 28*28))GradientTape训练方法
首先参考Keyird使用GradientTape训练的方法:
这里尽可能使用 tf 类中的函数,因为其函数大多都有优化,本次学到的新功能有:
-
使用
tf.constant或tf.convert_to_tensor将数据转化为tf.tensor数据类型,这种类型类似于np.ndarray,所以在某种程度上可以起到替代作用. -
dense_network.build(input_shape=(None, 28*28)),设置输入特征为28*28,而不是像以往将input_shape写到Sequential网络的第一层中. -
验证集也可以按照batch进行分割,每次判断一整个batch的正确率即可,而且batch越大,预处理速度越快,所以可以尝试将整个验证集放到一个batch中,减少了数据读入花费的时间:
test_ds = test_ds.batch(len(test_ds)). -
使用TF自带的记录器更容易判断结果的准确率:
tf.metrics.Accuracy()是最简的一种准确率测量器,可以用于比对对应标签是否相同. 好用但是一定要用对,两种写法上正确率问题就出在这里,下文会详细介绍记录器的使用方法.
# coding: utf-8
import tensorflow as tf
from tensorflow.keras import layers, optimizers, datasets, Sequential, metrics # 导入子库
from tqdm import tqdm
# 数据集读入
(x, y), (x_val, y_val) = datasets.mnist.load_data()
x = tf.constant(x, dtype=tf.float32)/255. # 转化为tensor,图像特征缩放为0~1
y = tf.constant(y, dtype=tf.int32) # 转化为tensor,标签
x_val = tf.constant(x_val, dtype=tf.float32)/255. # 转化为tensor,图像特征缩放为0~1
y_val = tf.constant(y_val, dtype=tf.int32) # 转化为tensor,标签
train_ds = tf.data.Dataset.from_tensor_slices((x, y)) # 构建数据对象
test_ds = tf.data.Dataset.from_tensor_slices((x_val, y_val)) # 构建数据对象
test_ds = test_ds.batch(len(test_ds)) # 将验证集打包为一个batch,预测速度大大增加
train_ds = train_ds.shuffle(1000).batch(32).repeat(10) # 打乱数据集,设置训练batch为32,重复10遍
batch_N = len(train_ds)
# 2. 网络搭建
dense_network = Sequential([
layers.Flatten(),
layers.Dense(256, activation='relu'),
layers.Dense(128, activation='relu'),
layers.Dense(10)
])
dense_network.build(input_shape=(None, 28*28)) # 设置输入特征为28*28
# 3.模型训练
optimizer = optimizers.SGD(lr=0.01) # 使用随机梯度下降法,学习率=0.01
acc_meter = metrics.Accuracy() # 准确率测量器,累计记录器
for step, (x, y) in enumerate(train_ds): # 输入一个batch数据进行训练
with tf.GradientTape() as tape: # 构建梯度记录环境
out = dense_network(x) # 输出 [b,10]
y_onehot = tf.one_hot(y, depth=10) # one-hot编码
loss = tf.reduce_sum(tf.square(out - y_onehot))/32. # 均方损失函数
grads = tape.gradient(loss, dense_network.trainable_variables) # 求loss关于网络中所有可训练参数的梯度
optimizer.apply_gradients(zip(grads, dense_network.trainable_variables)) # 更新网络参数
acc_meter.update_state(y_true=y, y_pred=tf.argmax(out, axis=1)) # 比较预测值与标签,更新准确率
if step % 200 == 0: # 每200个step输出一次结果
print(f"{'step='+str(step)+'/'+str(batch_N):<20} loss={loss.numpy():.4f}\
Accuracy={acc_meter.result().numpy():.4f}")
acc_meter.reset_states() # 准确率清空
# 4.验证集预测
pred_meter = metrics.Accuracy() # 准确率测量器
for x, y in tqdm(test_ds):
out = dense_network(x) # 输出 [b,10]
pred = tf.argmax(out, axis=1) # 预测结果[b,]
pred_meter(y, pred)
print('验证集准确率', pred_meter.result().numpy())这种写法训练集上的正确率为 96.86%,验证集上的正确率为 96.61%. (选用更小的学习率可以进一步提高到98%)
直接调用fit函数
该部分代码主要在数据的标签上做了些调整:
y = tf.one_hot(y, depth=10) # 转化为one-hot编码
y_evl = tf.one_hot(y_evl, depth=10) # 转化为one-hot编码其余部分为超参数配置,直接训练即可,详细请见代码
# coding: utf-8
import tensorflow as tf
import tensorflow.keras as keras
from tensorflow.keras import layers, optimizers, datasets, Sequential, metrics # 导入子库
(x, y), (x_evl, y_evl) = datasets.mnist.load_data()
# 训练集
x = tf.constant(x, dtype=tf.float32)/255. # 转化为tensor,图像特征缩放为0~1
y = tf.constant(y, dtype=tf.int32) # 转化为tensor,标签
y = tf.one_hot(y, depth=10) # 转化为one-hot编码
train_ds = tf.data.Dataset.from_tensor_slices((x, y)) # 构建数据对象
train_ds = train_ds.shuffle(1000).batch(32) # 打乱数据集,设置训练batch为32
# 验证集
x_evl = tf.constant(x_evl, dtype=tf.float32)/255. # 转化为tensor,图像特征缩放为0~1
y_evl = tf.constant(y_evl, dtype=tf.int32) # 转化为tensor,标签
y_evl = tf.one_hot(y_evl, depth=10) # 转化为one-hot编码
evl_ds = tf.data.Dataset.from_tensor_slices((x_evl, y_evl)).batch(32) # 构建数据对象
# 构建网络框架
dense_network = Sequential([
layers.Reshape(target_shape=(28*28,), input_shape=(28, 28)),
layers.Dense(256, activation='relu'),
layers.Dense(128, activation='relu'),
layers.Dense(10)
])
dense_network.build(input_shape=(None, 28*28)) # 设置输入特征为28*28
# 设定超参数进行训练
optimizer = optimizers.SGD(lr=0.01) # 使用随机梯度下降法,学习率=0.01
dense_network.compile(optimizer=optimizer, loss='MSE', metrics=['accuracy'])
dense_network.fit(x, y, epochs=10, validation_data=evl_ds)
print(dense_network.evaluate(evl_ds)) # 直接调用评估函数
# 手写验证集预测
meter = metrics.Accuracy()
for x, y in evl_ds:
out = dense_network(x) # 输出 [b,10]
pred = tf.argmax(out, axis=1)
y = tf.argmax(y, axis=1)
meter.update_state(y, pred)
print('验证集准确率', meter.result())运行代码发现训练集正确率为 92%,验证集正确率为93%.
发现问题
直接调用fit函数代码看上去很简单,但是出现了非常大的问题,那就是训练出来的准确率和loss函数值完全不同!!!而且准确率远低于直接使用GradientTape的写法,loss函数值也不相同. 直接使用fit的loss函数值基本在0.01的数量级,而GradientTape的loss函数值在0.1左右.
而且,最后手写验证集预测的正确率和直接调用评估函数的正确率相同,说明准确率的计算没有问题.
所以第一个问题:是否是TF自带损失函数MSE出了问题.
解决问题
我们直接考虑什么是MSE的工作原理,进行尝试可得下面两个相等及官方文档可知 :
a = tf.keras.losses.MSE([1,2,3],[0.5,1,1]).numpy()
b = (0.5**2+1**2+2**2) / 3
loss = mean(square(y_true - y_pred), axis=-1) # 官方文档那也就是假设两个向量 的维数均为 ,则 (表示欧氏距离)
由于损失函数只会作用在输出向量的最后一维上,也就是输出向量维数为 [b,10](b 表示batch_size),那么 MSE 返回值就是 [b,] 的向量,而不是标量. 但是我们需要的最终损失是一个标量,即这个损失的期望,也就是期望风险,如下定义
这里乘以 的原因是 MSE 错误计算了均值,除以了10,所以需要返回一个10.
我们对上述猜测进行验证,在GradientTape的第35行进行修改
loss1 = tf.reduce_sum(tf.square(out - y_onehot))/32. # 均方损失函数
loss2 = tf.keras.losses.MSE(y_true=y_onehot, y_pred=out) # 或者直接使用keras的MSE
loss2 = tf.reduce_sum(loss2) / 32. * 10.
print(loss1, loss2) # 结果一致这里错误的原因是:最后的输出层是一个10维向量,而MSE接受的输出应该是一个1维的数值,这样才能保证计算结果的正确性. 但显然预测一个数字效率是非常低的(标签的均值太大,网络训练速度非常慢),应该转化为one-hot编码进行预测,而MSE对one-hot编码值只会计算最后一维,所以直接在fit函数中使用MSE是有问题的,其计算的损失函数值会比真实的MSE计算出的结果小10倍
有两个简单的方法应对:
-
由于损失函数值小10倍,也就是梯度每次更新小10倍,所以只需要将学习率增大10倍即可,修改
optimizer = optimizers.SGD(lr=0.1)再次训练可得到正确率为 96% 解决问题. -
重写loss函数,同样可得到正确的 96% 正确率.(推荐使用该方法)
def my_MSE(y_true=None, y_pred=None): # 重写训练函数
return tf.reduce_sum(tf.square(y_true - y_pred)) / 32.
dense_network.compile(optimizer=optimizer, loss=my_MSE, metrics=['accuracy']) # 避免使用'MSE'为了弄清楚fit函数的原理,我们发现loss函数输出的结果是一个向量,于是fit函数应该是做了均值处理,写为GradientTape形式如下
loss = tf.keras.losses.MSE(y_true=y_onehot, y_pred=out) # 仅修改第一个代码的35行
loss = tf.reduce_mean(loss)得到的正确率为 93% 与直接调用fit的正确率相同
源代码分析
阅读fit函数中计算loss的源代码,发现在训练部分使用train_step进行训练,其中computer_loss函数用于计算loss,默认调用complied_loss返回Model.compile时定义的loss,然后complied_loss又是由LossesContainer类封装,这个封装类中第113行说明计算出的loss向量后均会使用keras.metrics.Mean进行均值处理,同样说明上述猜测正确.
# 直接调用fit计算loss的调用关系
Model.fit -> train_step -> compute_loss -> compiled_loss -> compile_utils.LossContainer(loss均值处理) -> ...
# 所以我们想要重写loss函数可以直接重载model.compute_loss函数即可重写fit函数
该方法的好处在于我们可以利用fit自带的许多callback功能,例如:tensorboard功能,用于可视化训练结果、网络框架,可以便捷的展示你的模型.
重写fit函数参考 TF指南 - 自定义Model.fit 内容,我们只需重写 train_step 和 test_step 函数,分别对应训练 Model.fit 和评估 Model.evaluate 函数. 在 train_step 中完成 GradientTape 过程即可,并返回loss函数和准确率的测量即可.
初始化部分沿用第一种 GradientTape 未将标签转化为one-hot编码形式
# coding: utf-8
import tensorflow as tf
import tensorflow.keras as keras
from tensorflow.keras import layers, optimizers, datasets, Sequential, metrics # 导入子库
from tqdm import tqdm
(x, y), (x_val, y_val) = datasets.mnist.load_data()
# 训练集
x = tf.constant(x, dtype=tf.float32)/255. # 转化为tensor,图像特征缩放为0~1
y = tf.constant(y, dtype=tf.int32) # 转化为tensor,标签
train_ds = tf.data.Dataset.from_tensor_slices((x, y)) # 构建数据对象
train_ds = train_ds.shuffle(1000).batch(32) # 打乱数据集,设置训练batch为32,重复10遍
# 验证集
x_evl = tf.constant(x_val, dtype=tf.float32)/255. # 转化为tensor,图像特征缩放为0~1
y_evl = tf.constant(y_val, dtype=tf.int32) # 转化为tensor,标签
evl_ds = tf.data.Dataset.from_tensor_slices((x_evl, y_evl)).batch(32) # 构建数据对象
optimizer = optimizers.SGD(lr=0.01) # 使用随机梯度下降法,学习率=0.01
def my_loss(y_true=None, y_pred=None): # 自定义损失函数
return tf.reduce_sum(tf.square(y_true - y_pred))/32.
class my_Sequential(keras.Sequential):
def __init__(self, layers=None, name='mySeq'):
super().__init__(layers=layers, name=name)
def train_step(self, data):
x, y = data
with tf.GradientTape() as tape:
out = self(x, training=True)
y_onehot = tf.one_hot(y, depth=10)
loss = self.compiled_loss(y_onehot, out) # 使用Model.compile()中的损失函数
grads = tape.gradient(loss, self.trainable_variables)
self.optimizer.apply_gradients(zip(grads, self.trainable_variables)) # 更新梯度
self.compiled_metrics.update_state(y, out) # 使用Model.metrics()中的测量器,更新正确率
return {m.name: m.result() for m in self.metrics} # 将返回的测量值用map打包
def test_step(self, data): # 与train_step部分完全类似,只是少了梯度更新,不用计算loss和grads
x, y = data
out = self(x, training=False)
y_onehot = tf.one_hot(y, depth=10)
loss = self.compiled_loss(y_onehot, out)
self.compiled_metrics.update_state(y, out)
return {m.name: m.result() for m in self.metrics}
dense_network = my_Sequential([
layers.Flatten(input_shape=(28,28), name='Input'),
layers.Dense(256, activation='relu', name='Dense1'),
layers.Dense(128, activation='relu', name='Dense2'),
layers.Dense(10, name='Output')
])
tb_callback = tf.keras.callbacks.TensorBoard(log_dir=r"logs/sgd/", histogram_freq=1) # 使用tensorboard记录回调信息
dense_network.compile(optimizer=optimizer, loss=my_loss, metrics=['accuracy'])
dense_network.fit(train_ds, epochs=10, validation_data=evl_ds, callbacks=[tb_callback]) # 在callbacks中加入tb_callback
dense_network.evaluate(evl_ds, return_dict=True) # 验证集预测训练集正确率为 97.05%,验证集正确率为 96.76%
遇到的问题
上述代码是没有任何问题的代码,在之前的编写过程中发现两个问题:
准确率计算出错
Model.compile 中 metrics 使用 accuracy 参数对应的测量器到底是什么?
- 参考Model.compile官方文档中metrics介绍,TensorFlow会自动根据数据集的标签和模型的输出自动选择三种不同的准确率测量器:
tf.keras.metrics.BinaryAccuracy, tf.keras.metrics.CategoricalAccuracy, tf.keras.metrics.SparseCategoricalAccuracy,这里是多维分类,只注重第二和第三种. 经过尝试发现,自动选择原理应该指的是第一次调用compiled_metrics时会确定下来,确定方法如下所示(分类器默认都是比较[b,*]除去第一维以外的信息,默认第一维是batch_size) - 第二个
CategoricalAccuracy多项-多项测量器,通过比对两个概率分布的最大值是否相同,如果y_true,y_pred最后一维都是向量时选择. - 第三个
SparseCategoricalAccuracy单项-多项测量器,通过比对一个标量是否是另一个概率分布的最大值,,如果y_true最后一维是常量,y_pred最后一维是向量时选择.
因为我们发现,如果直接使用 CategoricalAccuracy 对真实的标签计算精度准确率会大大下降,因为他会将全部的标签作为一个向量进行比对,也就是比对数目只有batch个,与 Accuracy 比较结果完全不同:
m = tf.keras.metrics.CategoricalAccuracy()
m.update_state([1,2,3], [1,2,2])
print(f"准确率: {m.result().numpy():.2f}, 总样本数目: {m.count.numpy()}")
# 准确率: 0.00, 总样本数目: 1.0
acc = tf.keras.metrics.Accuracy()
acc.update_state([1,2,3], [1,2,2])
print(f"准确率: {acc.result().numpy():.2f}, 总样本数目: {acc.count.numpy()}")
# 准确率: 0.67, 总样本数目: 3.0这第一种计算出的准确率大大低于第二种,所以我们只需要将
self.compiled_metrics.update_state(y, tf.argmax(out, axis=-1))对应CategoricallAccuracy测量器. 最终正确率仅有 91.79%,而且重新手写正确的测量器,对模型准确率测量得到正确率为 96% 说明就是测量器使用错误. 因为最后比较的是概率分布,所以这里的正确写法应该是self.compiled_metrics.update_state(y_onehot, out),y_true,y_pred维数均为[b,10], [b,10]self.compiled_metrics.update_state(y, out)对应SparseCategoricalAccuracy测量器. 最终正确率为 96.73%,没有错误.[b,], [b,10]
这里错误的使用测量器的主要原因在于,默认了 model.compile 中 accuarcy 参数会使用 Accuracy 度量器,但是他使用了 CategoricalAccuracy 度量器,这是以后要注意的问题,因为神经网络最后一层的输出一般为概率分布,所以对应的测量器一般都具有处理概率分布的过程,无需手动转换求预测值 tf.argmax(out, axis=-1).
ps. 调试fit内部的函数,要使用
tf.print()进行输出调试,因为整个过程是创建在计算图中的,正常
loss函数输出问题
第二个问题是在训练过程中,如果不使用compiled_loss计算loss值,直接在输出部分返回自己计算出的loss值:
def test_step(self, data):
x, y = data
out = self(x, training=False)
y_onehot = tf.one_hot(y, depth=10)
loss = tf.reduce_sum(tf.square(y_true - y_pred))/32. # 自己计算loss
self.compiled_metrics.update_state(y, out)
matrics = {m.name: m.result() for m in self.metrics}
matrics['loss'] = loss # 在返回的输出中加上loss
return matrics会发现输出的log中验证集的loss值总小于训练集的loss值,而且不是几个数量及倍数的关系.
但是在evaluate中的输出日志中的loss又是正确的,但是最终返回的log字典中loss又是错误的.
首先阅读计算validation_data损失值的计算方法,在train.py第1694行发现,计算validation_data的损失值就是从evaluate返回的log字典中求出来的. 所以问题出在log字典的值于自定义的loss值不同的原因(这里我的猜测是,由于没有使用compiled_loss,所以TF可能自行计算出compiled_loss对应的loss值返回回来,而这个默认的loss函数就正好是MSE,所以loss的均值特别小).
这里可能是因为没有自定义loss的测量器导致的,而loss的测量器一般都是取均值,所以为了保持简单,我们选择重写loss函数,然后导入到Model.compile中,这样还是能使用compiled_loss计算loss,而且无需在train_step中返回loss值,于是就有了上述的写法.
模型可视化
我们使用重写fit函数的目标就是为了使用Tensorboard来进行模型可视化,具体操作非常简单,参考TF指南 - 开始使用TensorBoard,只需在 Model.fit 的回调选项 callbacks 中加入 tf.keras.callbacks.TensorBoard(log_dir=dir_path, histogram_freq=1) 即可在文件夹 dir_path 中找到模型生成的日志,再使用cmd窗口输入 tensorboard --logdir dir_path 即可运行TensorBoard,cmd中会返回一个网址,从网页中打开即可.
我们这里分别创建两个log_dir路径,分别命名为 "logs/sgd/" 和 "logs/adam/" 用于比对两种优化器 SGD(lr=0.01) 和 Adam(lr=0.001) 的训练结果.
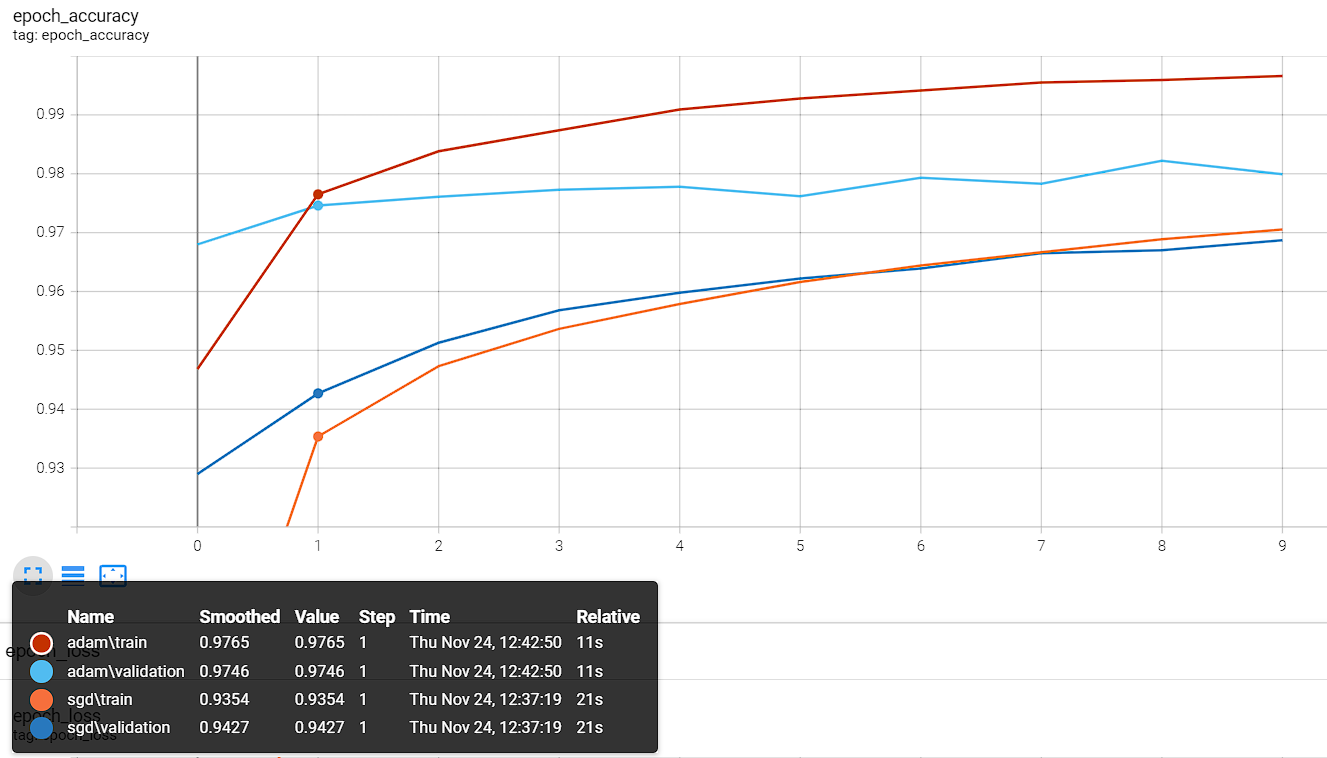
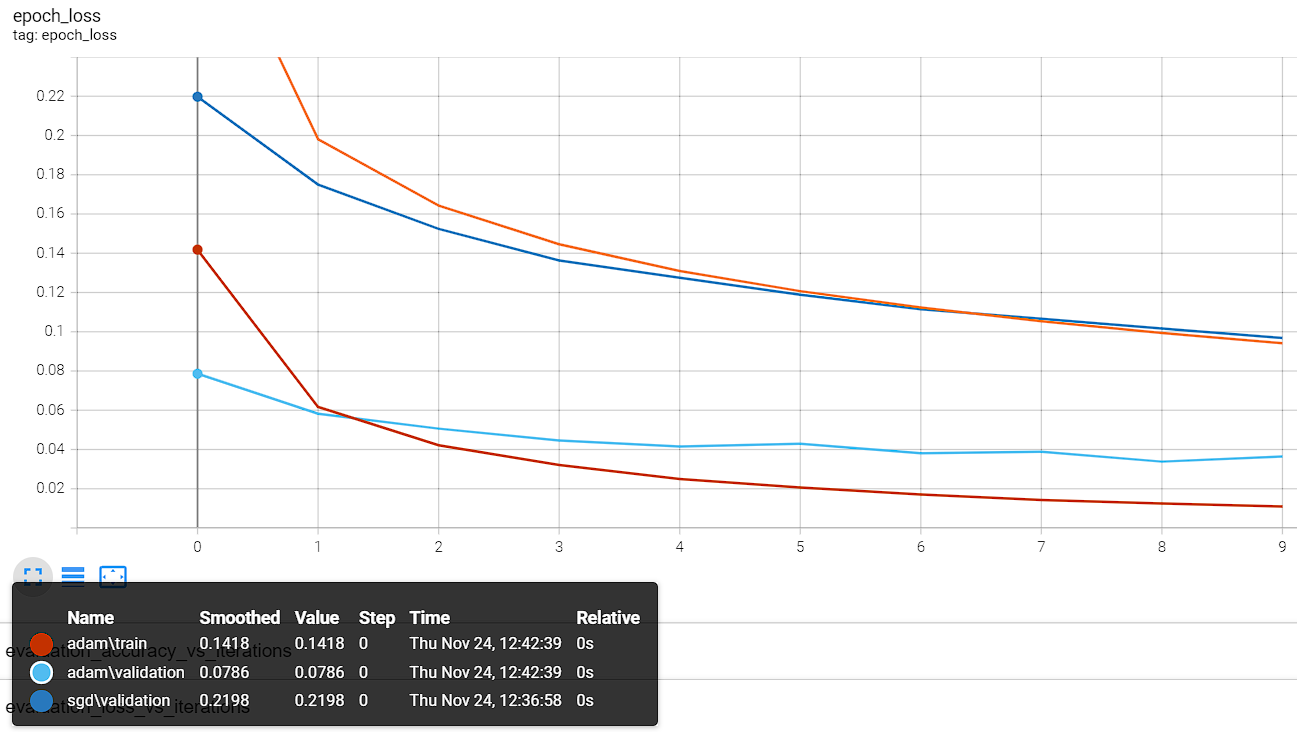
可以看出,adam 的训练效果非常好,同样的训练次数下,验证集都快过拟合了🤣,而且loss下降速度也更快.
在最上面Graphs一栏中,我们还能看到模型的计算图,非常直观
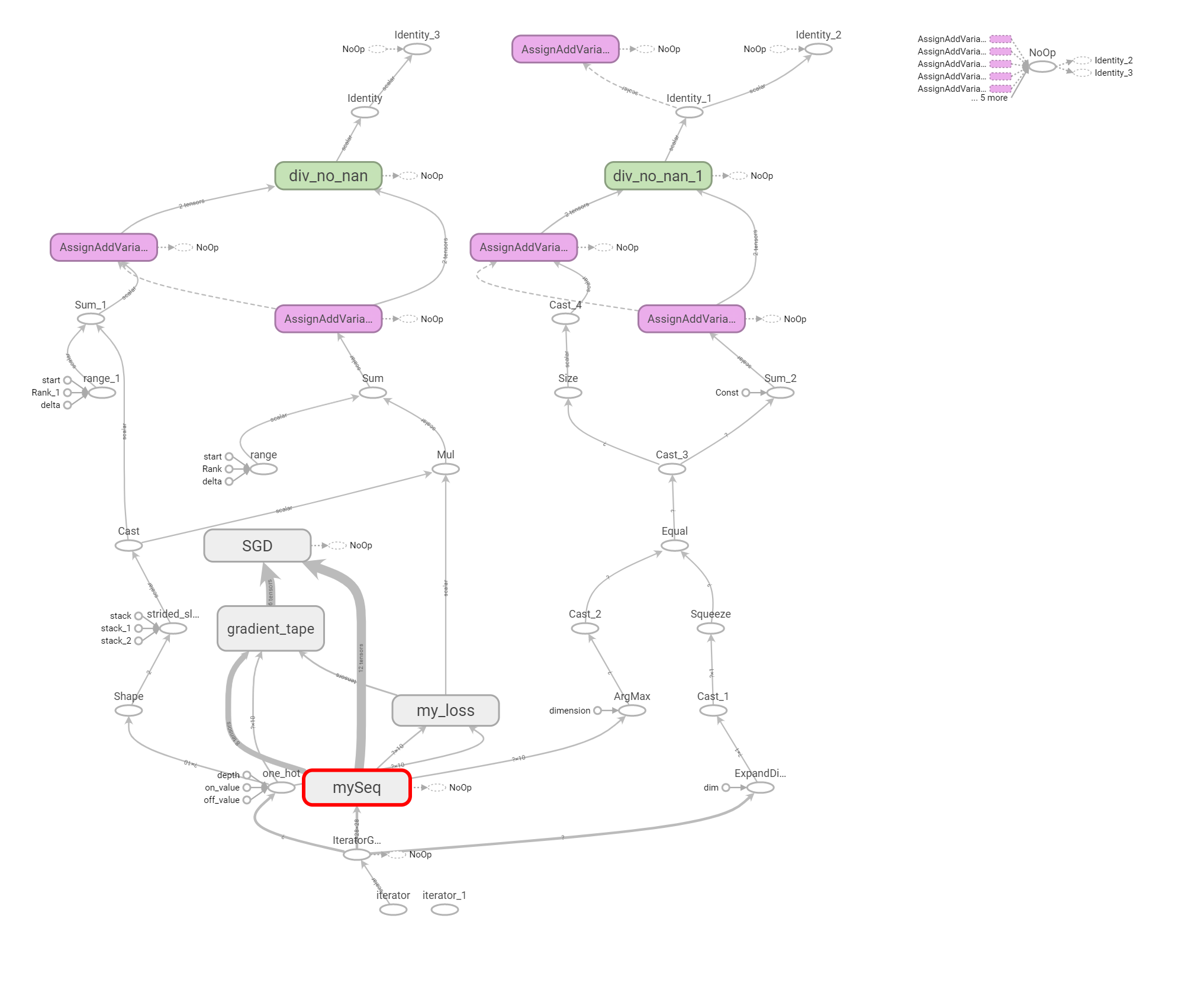
放大 mySeq 也就是神经网络主要结构部分,我们可以看到构建的神经网络框架,非常直观
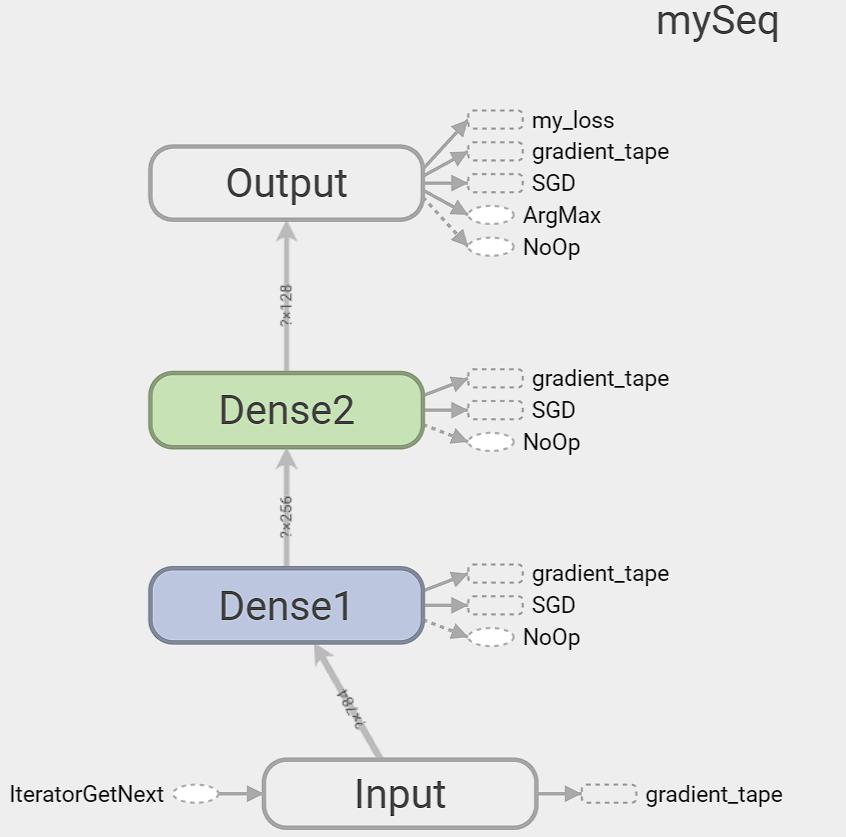
在Histograms一栏中,我们可以看到可学习参数的主要分布,可视化模型参数分布
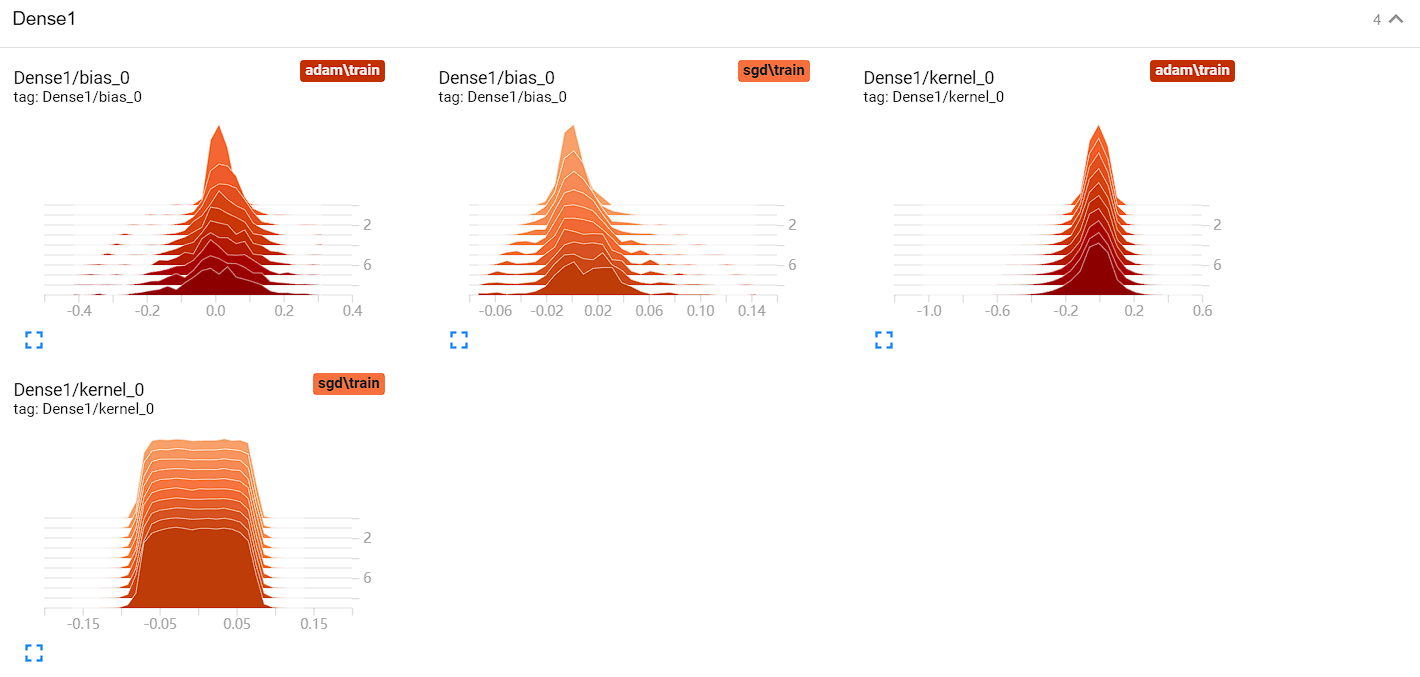
总之本次解决问题学习到了很多TF的可自定义函数,便于以后进行自定义模型构建,应该全部都会按照第三种重写fit函数的形式进行模型自定义,这样也能便于可视化模型,十分方便!