循环神经网络
简介
循环神经网络(Recurrent Neural Networks, RNN)是对前馈型全连接神经网络的改进. 全连接神经网络的输入维度在确定网络结构的时候已经固定,而且当特征之间具有的潜在关联性也无法解决. 循环神经网络支持输入任意长度的特征,并且可以通过处理特征之间具有的关联性,这也称为神经网络的记忆力.
一般的RNN具有短期记忆力,使用门控机制(Gating Mechanism)可以使其具有更长的记忆,例如LSTM和GRU,它们可以解决在长序列下发生的梯度爆炸和消失的问题,也称为长程依赖问题.
RNN
为解决前馈型全连接神经网络无法处理与输入顺序相关的特征输入,而通过加入短期记忆力可以解决该问题:使用带自反馈神经元处理任意长度的时序数据.
时序数据:有时间上相关性的数据,x1,x2,⋯,xt 有前后时间相关性,即在每个时刻 t 下,神经网络只能看到得到 t 时刻之前的全部数据,即 xt,xt−1,⋯,x1 的特征输入.
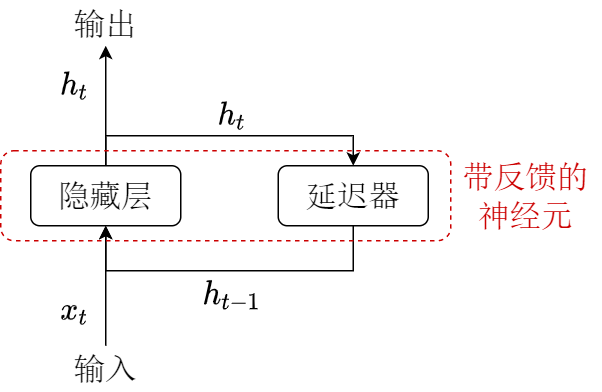
上图就是RNN的一般结构,看起来非常简单,我们可以将文字用数学符号表示,并将其展开如下图
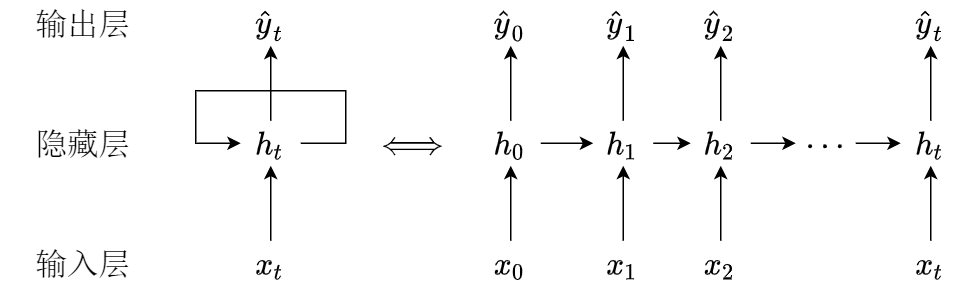
将隐藏层中神经元的活性值 ht 称为隐状态(hidden state),定义式为
ht={f(ht−1,xt),0,t⩾1,t=0.
其中 f(⋅) 为非线性函数,它可以是一个复杂前馈网络,也可以是一个简单的sigmoid函数. 对于不同的 f(⋅) 我们可以得到不同版本的RNN.
简单循环网络
简单循环网络(Simple Recurrent Network, SRN). 设 xt∈RM 为 t 时刻的输入,ht∈RD 为隐状态(活性值),则
⎩⎪⎪⎨⎪⎪⎧yt=Vhtzt=Uht−1+Wxt+bht=f(zt)
其中 U∈RD×D,W∈RD×M 为权重矩阵,前者也称为状态-状态矩阵(state to state),后者也称为状态-输入矩阵,b∈RD 为偏置向量,f(⋅) 为非线性函数(sigmoid或tanh). 如下图所示(方框为非线性变化)
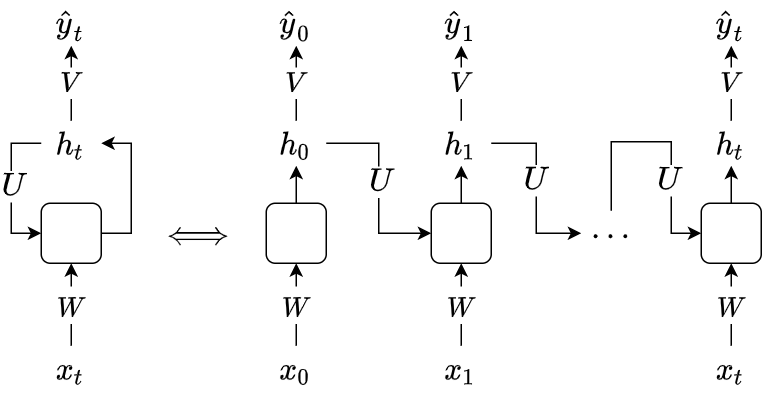
与RNN相关的两个定理,证明可参考相关论文. 大致含义就是RNN可以描述一个给定的空间中所有的点随时间状态变化的情况(动力系统).
定理1(RNN通用近似定理 Haykin):一个全连接RNN可以以任意准确率近似任一非线性动力系统.
定理2(Turing完备):一个使用sigmoid型激活函数的全连接RNN可以模拟所有图灵机(解决所有可计算问题).
RNN的应用
1. 文本分类(序列 - 类别)
样本特征:长度 T 的时间序列 x=(x1,⋯,xT)∈RT,标签:分类类别 y∈{1,2,⋯,c}. 可以将文本信息作为输入,然后将RNN的输出连接到全连接神经网络进行分类. 有两种网络结构如下图所示
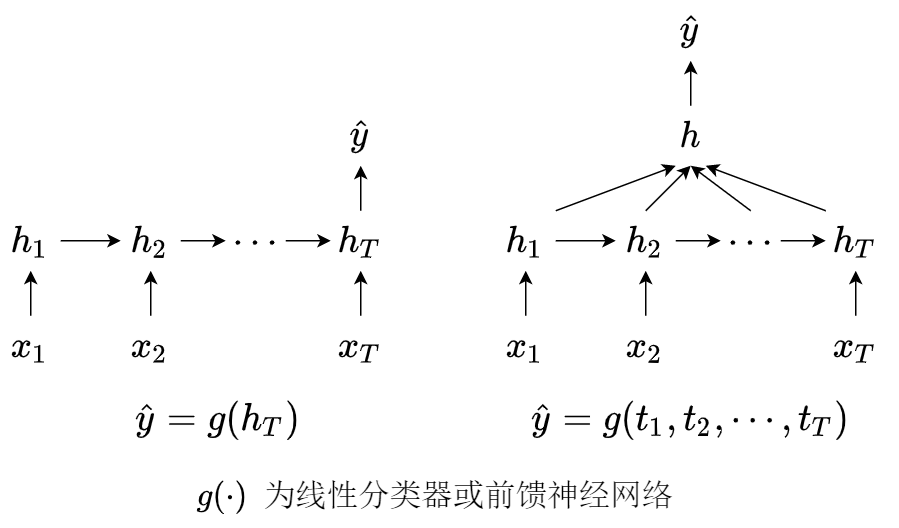
代码实现:语义识别 - 利用RNN判断电影评论是正面的还是负面的.
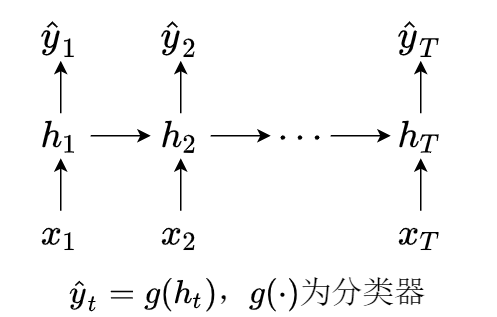
2. 词性标注(序列 - 序列,同步)
输入变量个数和输出变量个数一一对应,样本特征:长度为 T 的时间序列 x=(x1,⋯,xT)∈RT,标签:y=(y1,⋯,yT)∈RT. 网络结构如下图所示
3. 机器翻译(序列 - 序列,异步)
序列 - 序列网络结构也称为编码器 - 解码器(Encoder - Decoder),没有严格的对应关系,无需保持相同长度,样本特征:长度为 T 的时间序列 x=(x1,⋯,xT)∈RT,标签 y=(y1,⋯,yM)∈RM. 网络结构如下图所示
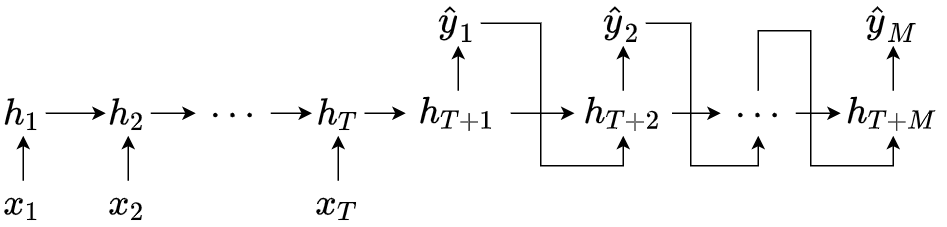
⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧ht=f1(ht−1,xt),hT+t=f2(hT+t−1,y^t−1),y^t=g(hT+t)h0=y^0=0.t∈[1,T],t∈[1,M],t∈[1,M],
长短期神经网络
长短期神经网络(Long Short Term Memory Network, LSTM),有简单RNN神经网络进行的变体,具有更长的记忆力. 由于简单RNN中,整个神经网络使用的是相同的权矩阵 U,由于 ht=f(Uht−1+Wxt+b),当 ∣∣U∣∣2<1 时,隐状态 ht→0 (t→∞)(梯度消失),当 ∣∣U∣∣2>1 时,隐状态 ht→∞ (t→∞) (梯度爆炸). 所以简单RNN无法获得两个更长时间差的隐状态之间的关联性. 为了解决这种问题,引入LSTM算法.
LSTM是一种引入门控机制(Gating Mechanism)的算法,遗忘门 ft,输入门 it,输出门 ot,新的内部状态 ct∈RD 用于线性循环信息传递,输出信息到外部状态 ht∈RD,c~t∈RD 为候选状态. 它们具有以下关系式:
⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧c~t=ft=it=ot=ct=ht= tanh(Wcxt+Ucht−1+bc), σ(Wfxt+Ufht−1+bf), σ(Wixt+Uiht−1+bi), σ(Woxt+Uoht−1+bo), ft⊙ct−1+it⊙c~t, ot⊙tanh(ct).⟺⎩⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎧⎣⎢⎢⎢⎡c~tftitot⎦⎥⎥⎥⎤=ct=ht= ⎣⎢⎢⎢⎡tanhσσσ⎦⎥⎥⎥⎤(W[xtht−1]+b) ft⊙ct−1+it⊙c~t, ot⊙tanh(ct).
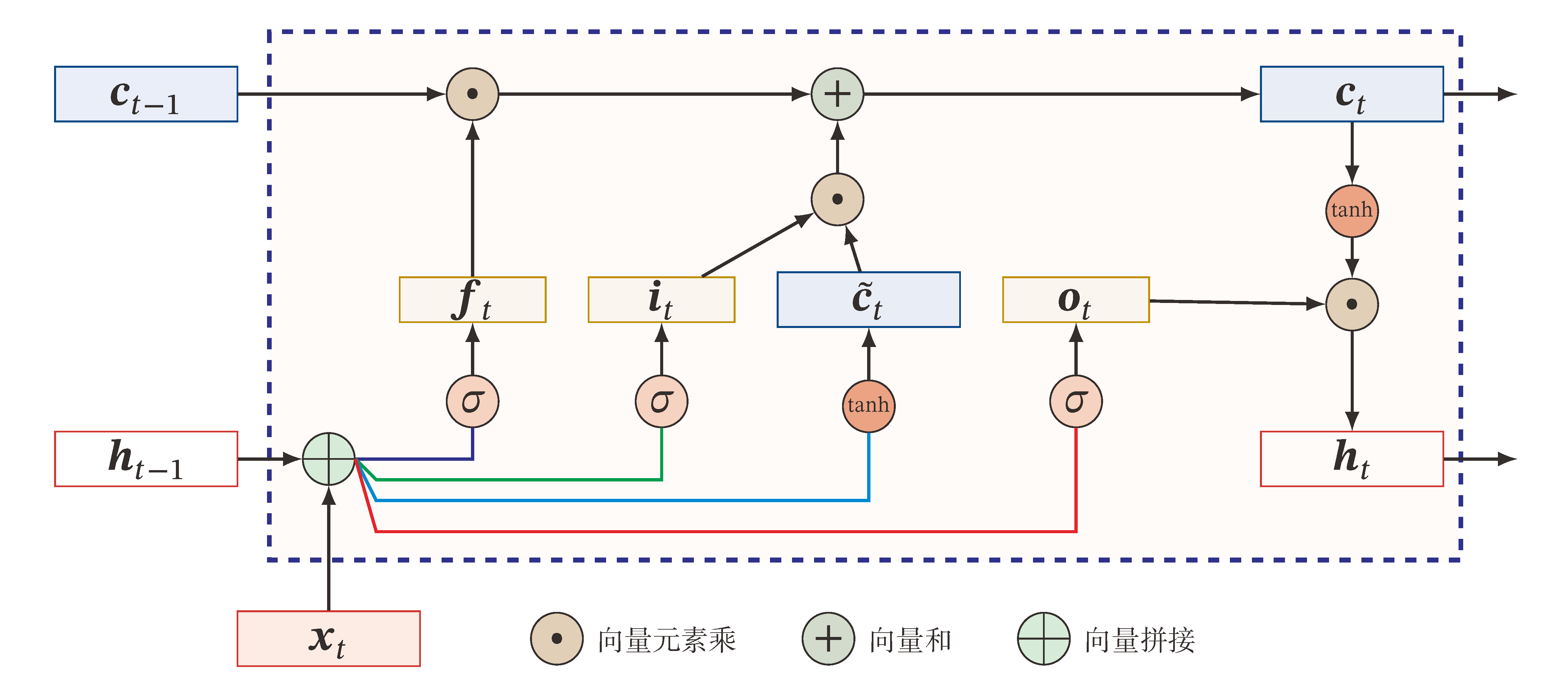
这里的门控机制并非传统的01门,而是一种“软”门,取值在 (0,1) 之间,用于信息的筛选,每个门都有各自的含义:
- 遗忘门 ft 控制上个时刻内部状态 ct−1 需要遗忘多少信息. 当 ft=0 时完全清空历史信息.
- 输入门 it 控制当前的候选状态 c~t 有多少信息需要保存. 当 ft=1,it=0 时完全复制上一个时刻的信息.
- 输出门 ot 控制当前的内部状态 ct 有多少信息需要输出到外部状态 ht.
这种算法只是增长了短期的记忆,将 ht 的更新周期加长,不是直接进行更新,而是通过中间记忆单元 ct 作为媒介减缓更新速度,但仍无法达到真正的长期记忆(保持极长时间的记忆),所以只能称为长短期神经网络.
代码实现
完整代码:音乐生成 - 利用RNN学习爱尔兰民谣曲谱进行作曲.
具体过程可以分为以下几步:
- 预处理数据集:
- 构建单词库
vacab,以频率高低设置对应索引,将字符串转为数字.
- 构建训练集batch,包含
sequence_length 和 batch_size 两个参数. 每个batch中的样本序列的开头 start 为 [0,n-len-1] 中随机选取的,其中 n=vacab_size 词库大小. 每个样本的特征为数据集的子串 [start, start+len-1],标签为子串 [start+1, start+len].
-
搭建模型:embedding层,参数 embedding_dimensionality → LSTM层,参数 rnn_units → Dense层,参数 units=vacab_size.
-
定义损失函数,使用交叉熵函数. 超参数配置:training_iterations,learning_rate. 构建训练函数:
- 使用
tf.GradientTap 对变量进行观测,计算 L(y,y^).
- 求出 ∂W∂L,W 为全体可学习参数
model.trainable_variables.
- 使用
optimizer 对梯度进行更新.
- 开始训练:执行训练函数
training_iterations 次,用 tqdm 可视化进度条,在记录点保存模型.
- 生成歌曲,根据启动种子
start_text 作为预测序列的开头,用 tf.random.categorical 以输出的结果作为概率分布选出一个预测值,作为下一次预测的输入值.






