线段树
线段树操作
线段树二分询问
UVA - 11525 - Permutation,SPOJ - NKMOU - IOI05 Mountains,UVA - 12419 - Heap Manager
本质就是利用线段树是二叉树的性质,如果某个区间信息具有单调关系,那么就可以通过判断左右儿子节点中该信息的大小,判断进入哪个儿子节点。线段树的二分询问一般是要求整个区间上最左或最右侧的某个解,通过维护前缀信息或后缀信息实现(取出前k大的节点)。
区间上(下)界限制操作
区间上(下)界限制操作就是对区间 ,将其中每个值进行上界为 的限制,即 ,我们直接考虑究竟有哪些区间节点(树上节点)会被修改,为了使得修改的点数目可控,期望只有最大值(如果是下界限制就是最小值)被修改,而不是多种。
考虑记录下每个区间节点的区间最大值 和区间次大值 ,要求 ,如果该区间中只有一种值,那么 。所以我们要修改的区间只有一种:,考虑在目标区间 中通过递归搜索这样的区间,然后对其最大值进行修改,如果发现修改后 ,那么还需继续向下搜索更新 。
实现方法
对于区间 的上界限制操作,具体实现方法如下:
- 在树上递归地找 的子区间 ,满足 (这里有一个剪枝,如果 则无需进一步递归其子区间,因为一定当前的上界 已经比整个区间的最大值都要大,不可能对任何节点的值进行限制;如果 说明需要进一步递归其子区间)
- 找到满足 的子区间后,将 减小到 ,如果发现 ,则还需进一步递归更新 。
在代码实现中,其实第二步当 时,没有直接递归更新 ,而是等待下一次更新,如果有比 更小的上界限制,才进一步递归更新 (这样可以少写一个更新函数)。
如果只有区间上界限制这一个操作,那么可以只记录一个 懒标记,用于将最大值直接限制到 上,如果和区间加法放在一起,那么就要在加上一个 操作,不过这样做有些复杂,我们考虑将最大值限制转化为区间加法(只不过是只对最大值存在的区间进行加法),设一下两个区间操作:
add1:区间最大值的区间加法懒标记。add2:区间非最大值的区间加法懒标记。
在 pushdown 操作中,我们只需判断当前节点的最大值是从哪个儿子转移上来的,由于当前节点的最大值可能已经被修改了,所以直接 mx1 = t[ls].mx1 + t[rs].mx1,如果 mx1 = t[ls].mx1 说明是从左儿子转移上来的,于是用 add1 懒标记进行更新 t[ls].add(add1),否则使用 add2 懒标记进行更新 t[ls].add(add2)。这里的更新操作 .update 就无需多言,和之前的区间加法无太大区别。
struct Node {
void push_lazy(Node &s, int ismx) {
if (ismx) s.add(add1, add1_, add2, add2_);
else s.add(add2, add2_, add2, add2_);
}
};
void pushdown(int p) {
int mx1 = max(t[ls].info.mx1, t[rs].info.mx1);
t[p].push_lazy(t[ls], mx1 == t[ls].info.mx1);
t[p].push_lazy(t[rs], mx1 == t[rs].info.mx1);
t[p].reset_lazy();
}如果还要维护区间历史最大(小)值,那么还需额外记录一下两个:
add1_:区间最大值的最大区间加法懒标记。add2_:区间非最大值的最大区间加法懒标记。
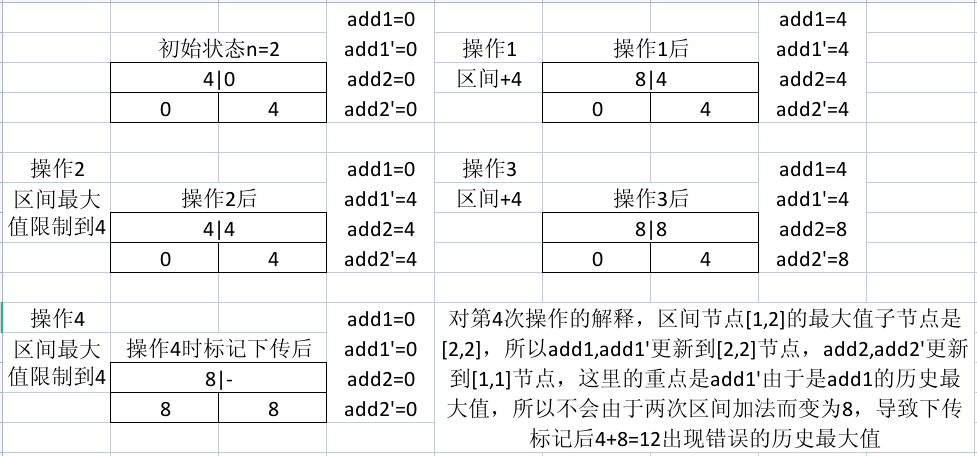
因为我们知道区间历史最大值就是记录下最大的懒标记就行,那为什么还要分最大和非最大区间呢?可以从下面例子中体会:(4|0 表示区间最大值为4,次最大值为0,其他节点类似,此处操作2后 4|4,还体现出了最大值和次最大值延迟下传的情况)
时间复杂度证明
我们先按照上述实现方法进行操作,即进行上界限制后,仍要保持 。
定理1:上界限制操作的均摊复杂度为 。(其中 为区间大小)
证明:这里从值域上进行证明,则值域大小的最大值为 (每个值的初值均不相同),如果进行一次上界限制 ,则值域大小一定会减小,假设当前整个值域上的最大值为 ,可以画出以下值域的示意图:

不妨令 (不然不会更新任何点),记区间中所有值在 中间的点的个数为 ,即
下面证明,该次操作的时间复杂度为 。
-
若 ,则最坏时间复杂度为单点修改,总共 。(如果某个区间节点的 则可以一直递归更新到子节点)
-
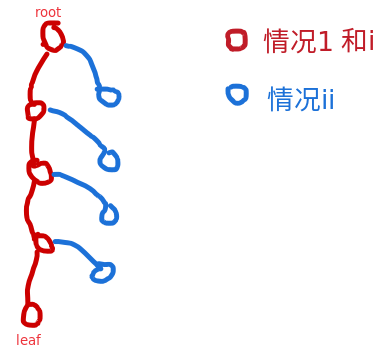
若区间节点的最大值为 ,记该区间节点的最大/次大值分别为 ,分两类情况:
i. 若 时,则该节点一定在 1 的某个叶子节点的更新路径上,用时包含在 1 中。
ii. 若 时,只需将 ,也就是只对最大值进行限制即可,因为限制后仍满足最大与次大值不同,所以无需进一步向下递归。这一部分的搜索,是 1 中搜索链中,每个点额外搜索的一个节点(因为每次向下更新会更新左右儿子节点,ii 的情况,只会出现在某个儿子节点中)
假设第 次操作修改了在 中的 个节点,那么下一次的值域上界 ,由于值域大小至少为 ,所以
又由于每次修改 个点时间复杂度为 ,所以,总时间复杂度为
区间历史和
洛谷 - U216697 线段树区间历史版本和,XJTUPC2023 - #1387. 大秦酒店欢迎您。
每个节点需要将当前和 sum 和历史和 sum_ 区分开,并且同时维护这两个信息,其实可以容易想到 sum 的所有相关标记 sum_ 一定至少要有,并且还要知道在标记下传前一共历史操作作用了多少次 tv。
详细地说:使用区间历史懒标记 tv 来记录懒标记下传前有多少个区间和sum没有更新到历史和sum_中,由于本题还有对区间加法操作,所以需要区间加法的懒标记 addv,对应历史区间加法懒标记 addv_,因为要记录该懒标记有多少次没有更新到下面的区间中,这种多标记更新的方法写一个更新函数更加方便 update(k, k_, t) 表示区间加法修改量k,历史加法修改量k_, 区间历史懒标记t,也就是有多少个当前节点的 sum 和 addv 还没更新到历史中去,最关键的就所有的历史更新addv_,sum_是要优先于当前addv,sum的更新之前:
void update(LL k, LL k_, int t) { // Info区间信息更新
sum_ += k_ * len + sum * t; // 历史更新优先于当前区间更新
sum += k * len;
}
void update(LL k, LL k_, int t) { // TNode树上节点更新
info.update(k, k_, t);
tv += t;
addv_ += addv * t + k_; // 历史懒标记更新优先于当前懒标记更新
addv += k;
}线段树合并
主要在SAM的endpos集合合并上的应用:字符串 - 后缀自动机 - 维护endpos集合。
线段树模板
基本上所有线段树的信息都可以分为三个结构体,Info节点信息,TNode树上区间节点,SEG线段树主程序。
静态线段树
一些基础操作练习题(前缀、后缀、最值、区间和维护等):
简单:UVA - 12299 - RMQ with Shifts - 单点修改,UVA - 1455 - Kingdom - 线段树区间修改+单点查询+并查集,UVA - 11992 - Fast Matrix Operations 线段树区间修改区间多目标查询
较复杂:UVA - 1400 - “Ray, Pass me the dishes!” - E10! 动态区间查询最大连续和
struct Info {
int len; int sum, mx, mn, ...; // 所有用到的区间信息,区间和sum,区间最值...
void update(int k, int v...) { // 区间信息更新,与题目操作对应,区间加的变量k,区间赋值v...
sum = ...; // 对区间信息进行更新
mx = ...;
...
}
Info operator + (const Info &rhs) const { // 区间合并,pushup和query上传时用到
return Info{len + rhs.len, sum + rhs.sum, sum_ + rhs.sum_};
}
};
struct TNode {
int l, r; int addv, setv, ...; // 懒标记
Info info; // 区间信息
void update(int k, int v, ...) { // 区间节点更新,与Info.update入参保持一致
info.update(k, v, ...); // 对区间信息进行更新
addv = ...; // 区间懒标记更新
setv = ...;
...
}
void push_lazy(TNode &s) { s.update(addv, setv, ...); } // 懒标记下传到子节点(如果对子节点有不同的下传方法,在此处自定义,例如区间上限限制操作中下传就要分是否是最大值子区间)
void clear_lazy() { addv = 0, setv = INF, ...; } // 懒标记重置
};
struct SEG {
TNode t[maxn<<2];
void pushdown(int p) {
t[p].push_lazy(t[ls]);
t[p].push_lazy(t[rs]);
t[p].clear_lazy();
}
void pushup(int p) { t[p].info = t[ls].info + t[rs].info; }
void build(int p, int l, int r) {
t[p] = TNode{l, r, 0, ..., {r-l+1, 0, ...}};
if (l == r) return;
int mid = (l+r) >> 1;
build(ls, l, mid), build(rs, mid+1, r);
}
void update(int p, int l, int r, int val) {
if (t[p].l == l && t[p].r == r) { t[p].update(val, ...); return; }
pushdown(p);
int mid = (t[p].l+t[p].r) >> 1;
if (r <= mid) update(ls, l, r, val);
else if (l > mid) update(rs, l, r, val);
else update(ls, l, mid, val), update(rs, mid+1, r, val);
pushup(p);
}
Info query(int p, int l, int r) {
if (t[p].l == l && t[p].r == r) return t[p].info;
pushdown(p);
int mid = (t[p].l+t[p].r) >> 1;
if (r <= mid) return query(ls, l, r);
else if (l > mid) return query(rs, l, r);
else return query(ls, l, mid) + query(rs, mid+1, r); // 区间信息合并
}
}seg;
动态开点线段树
SPOJ - NKMOU - IOI05 Mountains,UVA - 12419 - Heap Manager,UVA - 1232 - SKYLINE
使用动态开点线段树一般是要满足一下两个条件:
- 有默认的区间初值(例如全部初始化为0)
- 区间大小 非常大(例如 ),动态开点线段树时间复杂度主要和操作数有关
struct Info { int len; int sum, mx, mn, ...; void update(...){...} }; // 与静态线段树重复部分略去
struct TNode {
TNode *ls, *rs; // 子节点指针
int l, r, val; int addv, setv, ...; // 懒标记
Info info; // 区间信息
TNode(int l, int r, int val):l(l),r(r),val(val) { clear_lazy(); info = Info{r-l+1, ...}; } // 区间节点初始化一定是叶子节点,每个点具有相同的val
bool isleaf() { return !ls && !rs; } // 判断是否是叶子节点,其实只用判断ls和rs其中一个即可
void create() {
if (!isleaf()) return;
int mid = (l+r) >> 1;
ls = new TNode(l, mid, val);
rs = new TNode(mid+1, r, val);
}
void del() { if (ls) delete ls; if (rs) delete rs; ls = rs = nullptr; }
~Node() { del(); } // 析构函数,可递归删除整棵树 delete seg.rt
void update(int k, int v, ...) { ... } // 如果有区间值重置为统一值,可删除其子节点,回收内存
void push_lazy(TNode &s) { s.update(addv, setv, ...); } // 懒标记下传
void clear_lazy() { addv = 0, setv = INF, ...; } // 懒标记重置
};
struct SEG {
TNode *rt;
void pushdown(TNode &p) {
p.create(); // 若子节点不存在,则需创建
p.push_lazy(p.ls);
p.push_lazy(p.rs);
p.clear_lazy();
}
void pushup(TNode &p) { p.info = p.ls.info + p.rs.info; }
void build(int n) {
if (rt) delete rt;
rt = TNode{1, n, 0, ..., {n, 0, ...}}; // 只需创建一个根节点即可
}
void update(int l, int r, int val) { update(rt, l, r, val); }
void update(TNode &p, int l, int r, int val) {
if (t[p].l == l && t[p].r == r) { p.update(val, ...); return; }
pushdown(p);
int mid = (p.l+p.r) >> 1;
if (r <= mid) update(*p.ls, l, r, val);
else if (l > mid) update(*p.rs, l, r, val);
else update(*p.ls, l, mid, val), update(*p.rs, mid+1, r, val);
pushup(p);
}
Info query(int l, int r) { return query(rt, l, r); }
Info query(TNode &p, int l, int r) {
if (t[p].l == l && t[p].r == r) return p.info;
pushdown(p);
int mid = (p.l+p.r) >> 1;
if (r <= mid) return query(*p.ls, l, r);
else if (l > mid) return query(*p.rs, l, r);
else return query(*p.ls, l, mid) + query(*p.rs, mid+1, r); // 区间信息合并
}
}seg;
可持久化线段树
在原数组的每个位置上都按照前缀和加入到该位置的线段树中,因为每个位置都是基于前面一颗线段树基础上加入一个新的值,并且如果没有修改的部分就原封不动继承下来即可,所以每次更新复杂度就是(树的高度向上取整),总共要加入个节点,所以总时空复杂度上限就是,动态开点的数组大小就开成即可。有一些细节部分需要注意(主要是在指针使用时判断是否为空):
const int maxn = 2e5 + 10;
struct TNode { // 无需存储左右端点了,因为没有区间查询
TNode *ls, *rs; int sum;
void init() { ls = rs = nullptr; sum = 0; }
};
template <const int maxn, const int LOG = 19> // 1<<LOG >= 2*maxn
struct WSegmentTree {
int sz; TNode t[maxn * LOG];
void init() { sz = 0; }
TNode* new_node() { t[sz].init(); return &t[sz++]; }
void pushup(TNode &p) { p.sum = (p.ls ? p.ls->sum : 0) + (p.rs ? p.rs->sum : 0); }
TNode* update(TNode *p, int l, int r, int k) {
TNode &np = *new_node();
if (p) np = *p;
if (l == r) { np.sum++; return &np; }
int mid = (l+r) >> 1;
if (k <= mid) np.ls = update(p ? p->ls : p, l, mid, k);
else np.rs = update(p ? p->rs : p, mid+1, r, k);
pushup(np); return &np;
}
int query(TNode *p1, TNode &p2, int l, int r, int k) {
if (l == r) return l;
int dl = 0;
if (p1 && p1->ls) dl -= p1->ls->sum;
if (p2.ls) dl += p2.ls->sum;
int mid = (l+r) >> 1;
if (k <= dl) return query(p1 ? p1->ls : p1, *p2.ls, l, mid, k);
else return query(p1 ? p1->rs : p1, *p2.rs, mid+1, r, k-dl);
}
};
WSegTree<maxn> seg;
TNode *rt[maxn]; // 记录根节点
int main() {
...// 如果值域太大记得离散化
// 构建
rep(i, n) rt[i] = seg.update(i ? rt[i-1] : nullptr, 0, n-1, id(A[i]));
// 查询区间[l,r]
printf("%d\n", id2A[seg.query(l ? rt[l-1] : nullptr, *rt[r], 0, n-1, k)]);
...
}