YOLO9000: Better, Faster, Stronger(YOLOv2), YOLOv3: An Incremental Improvement
非常好的视频讲解:YouTube - ML For Neerds - YOLO OBJECT DETECTION SERIES
全部代码,自己用JAX+Flax+Optax实现,仅在数据读入处使用TensorFlow,从零开始实现YOLOv3,包括模型预训练和全模型训练:GitHub - KataCV/yolov3
YOLOv2, YOLOv3
在YOLOv2的基础上对YOLOv1进行了非常多细节上的改动,而YOLOv3则对网络架构进一步改进(Gauss金字塔),从而得到性能极强的YOLOv3。同时它的识别速度极快,我在JAX上进行复现,对视频文件进行处理过程中发现,模型的识别速度竟然有447fps,最终剪辑速度为92fps(被视频读取速度所限制,GPU为RTX4080),在CPU上的识别速度只有4fps(CPU为R7 4800U)。
值得一提的是YOLOv3是YOLO发明者Joseph Redmon目前所发表的最后一篇论文(2018/04/08),在这篇论文的最后一段讲述了其原因在于:当前的目标识别技术被商业化用于捕捉客户的隐私数据、被军方投入武器使用当中。这使得作者放弃了对YOLO系列的进一步改进,不过后续也有很多版本,当前已更新到YOLOv8,不过只有YOLOv4是学术研究,后面所有的版本均带有公司版权以商业化作为目的(例如YOLOv5是美团做的)无法直接使用。
并且,通过学习YOLOv4,本质上其对YOLOv3的核心框架没有任何更改,只是对其进行了大量细节上的微调,同时保证速度不降的前提下,使得mAP提升了10%左右。所以如果想做YOLOv4,一定先要研究清楚YOLOv2和YOLOv3。
下面我们逐步分析YOLOv2和YOLOv3中进行的改进。
定义及思路
设 S∈N+ 表示当前网格划分大小(Split size),C 为预测的总类别数,AS 为网格大小为 S 时的锚框(Anchor bounding box)集合。
在YOLOv3中加入了**锚框(Anchor bounding box)**这样的一个概念,这个概念是R-CNN中使用到的,也就是对边界框的大致形状的一个估计,这个锚框是通过对全体边界框做K近邻得到的(以负的相对IOU作为距离衡量标准),最后的模型预测也要从直接对边界框的宽高进行预测,转为对锚框的宽高相对比例进行预测。
在YOLOv3中,会在 3 个不同而缩放尺度(scale)下每个网格(cell)分别预测出 3 个相对于锚框的边界框。以下图为例(图片由自己写的数据集预处理代码生成[GitHub]):
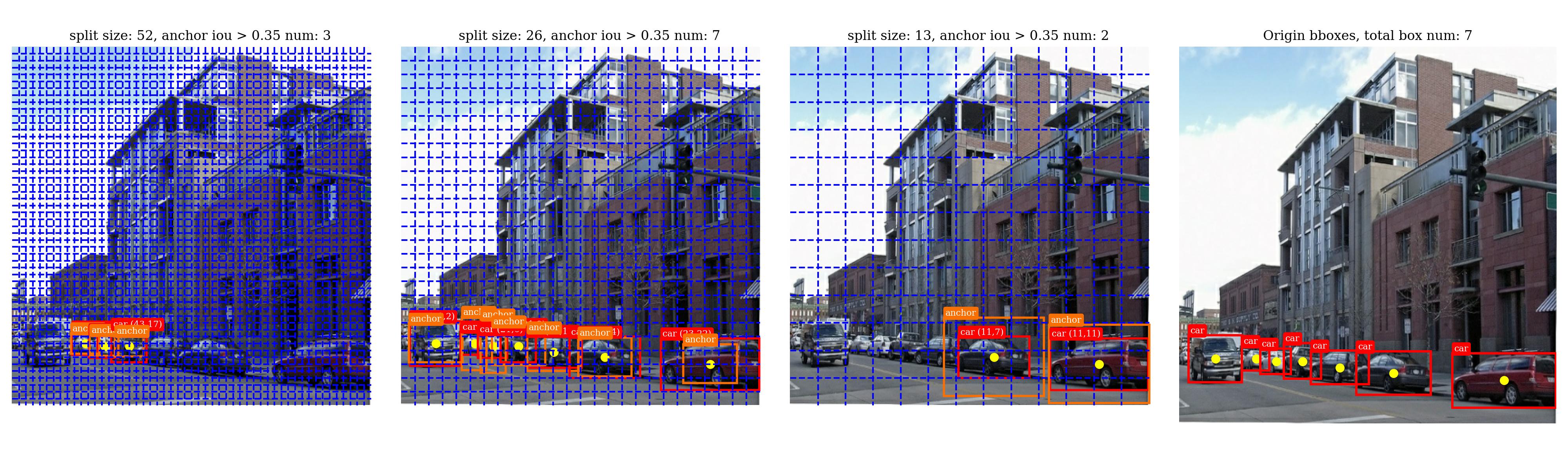
这里的网格划分的概念和YOLOv1一致,也就是我们会将每个框正中心所属的网格作为对该框进行预测的网格。在YOLOv1中我们每个网格上会预测2个边界框,而YOLOv3中我们会预测3个边界框,并且宽高是相对于合适大小的锚框的,见下文。
最右侧的是原图以及其中的所有待检测的边界框,左边三个分别是在3个不同网格大小下的和真实框最接近的锚框(这里我只显示了 IOU>0.35),从CV的知识可以知道,对于分辨率越高的图像细节的信息越多能易于识别小目标(左边第一个),对于分辨率越低的图像细节丢失越多易于识别大目标(左边第三个),所以我们将锚框大小从小到大平均分配到分辨率从大到小的图像检测当中,我们希望模型能在高/低分辨率下利用小/大锚框检测出上图左边第一/三个图片中的所有目标。
假设我们有下述9个锚框(论文中提供了右侧的像素大小,应该是根据COCO数据集在416×416分辨率下做K=9近邻的得到的,但是这具有一般性,所以我在PASCAL数据集上也用的是这9个锚框):
anchors = [ # 锚框的宽高相对整个图片的宽高比例
(0.02, 0.03), (0.04, 0.07), (0.08, 0.06), # (10, 13), (16, 30), (33, 23), # in 416x416
(0.07, 0.15), (0.15, 0.11), (0.14, 0.29), # (30, 61), (62, 45), (59, 119),
(0.28, 0.22), (0.38, 0.48), (0.90, 0.78), # (116, 90), (156, 198), (373, 326)
]
假设我们也有 3 个不同的网格划分大小 S∈{52,26,13},那么我们就可以依照分辨率与锚框大小成反比的关系对锚框进行分配:
A52=A26=A13= {(0.02,0.03),(0.04,0.07),(0.08,0.06)} {(0.07,0.15),(0.15,0.11),(0.14,0.29)} {(0.28,0.22),(0.38,0.48),(0.90,0.78)}
这也正是上图中每个网格划分下的锚框大小。我们比较下YOLOv1和YOLOv3总共会预测的边界框数目:
Npredict bbox={2⋅72=98,3⋅(522+262+132)=10647,YOLOv1,YOLOv3.
然而如何让模型能够看到不同分辨率下的图像呢?这就需要对网络的设计了(下一部分会详细介绍)。
网络设计
下图是一个非常清晰的网络架构,来自 知乎 - Algernon:
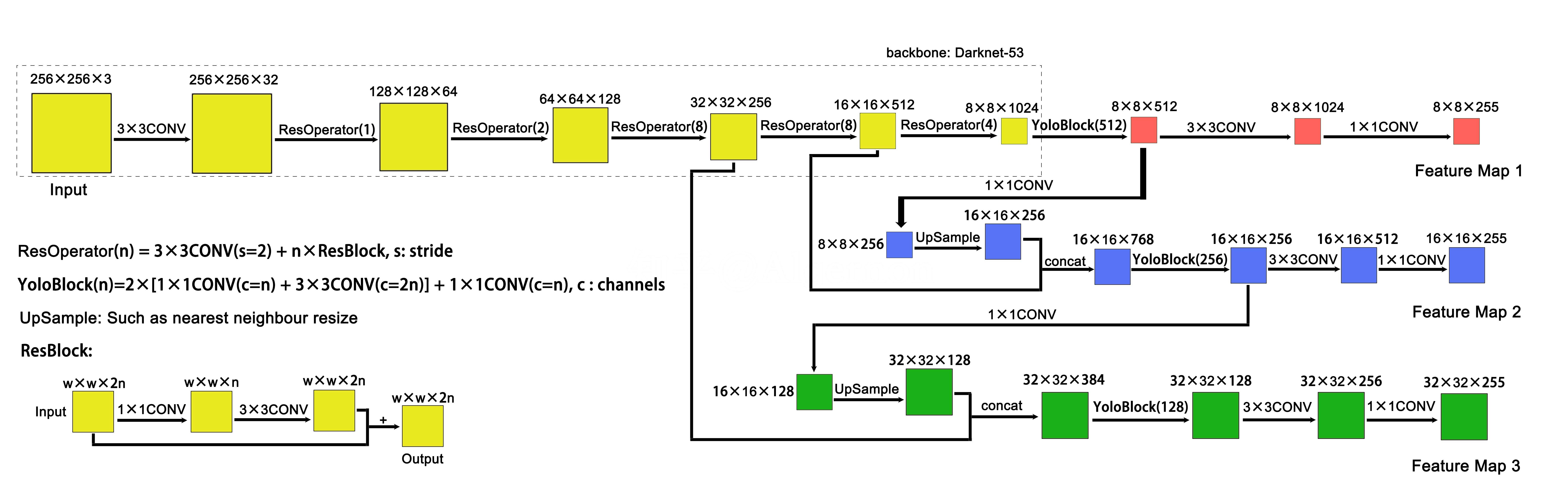
代码:自己实现的GitHub - (JAX)DarkNet-53 预训练和GitHub - (JAX)YOLOv3-model 完整模型,也有别人用PyTorch实现的GitHub - (PyTorch)YOLOv3-model
DarkNet-53
左上角虚线框内为骨干层backbone作者称之为DarkNet-53(黑暗骑士🤣),在Imagenet上进行预训练所需的全部卷积层和全连接层总共 53 层,使用的激活函数均为 leaky_relu(k=0.1),全部非输出处的卷积块都为 Conv + BatchNormalize + leaky_relu(0.1)。
注意在有 BN 层的时候无需对 Conv 加上多余的偏置,因为 BN 中的偏置能起到相同作用,BN论文中3.2段进行了解释。
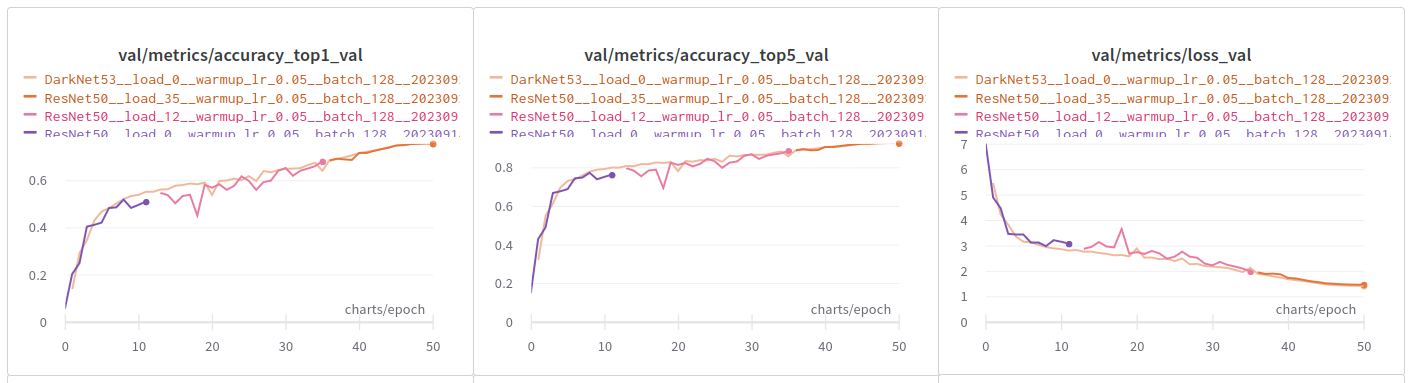
训练结果可以直接查看wandb分享的网页 ImageNet Result
Neck
Neck这个概念来自YOLOv4,他们将骨干层后续网络成为Neck,表示对特征的进一步聚合。在上图中就是除了虚线框外的所有部分,这个输出正好构成Gauss金字塔,由论文Feature Pyramid Networks for Object Detection(FPN)提出,再对每个不同scale下的结果分配不同的anchors进行预测(后续对FPN还有许多改进,例如PAN, NAS-FPN…,在YOLOv4中就是使用了PAN进行特征聚合)
Outputs
上图中的输入图像大小为 256×256×3,这个并不是论文中设计的输入大小,在YOLOv2论文中要求,最后的特征输出宽高必须为奇数(为了保证位于中心处的边界框有从属的网格),所以他设计的输出为 13×13,图像的输入大小为 416×416,经过上图网络的输出,三个尺度下的特征大小应该为 52×52,26×26,13×13。
输出的特征维度为 255 原因在于:B(5+C)=255, (B=3,C=80),B 为每个尺度下每个网格需要预测的边界框数目(也是所分配的锚框数目),C 为中目标类别数。我们可以将最后一个维度进一步划分为 (B,5+C),其中前 5 个变量表示 (c,x,y,w,h) 后 C 个变量表示对所属类别的概率分布 {pc}。(进一步解释请见下一部分)
模型预测
以 416×416×3 的图像输入为例,则网格划分大小分别为 S∈{52,26,13},下面分别对每个尺度单独进行讨论,由于每个尺度下都分配了 3 个锚框 AS,且 S 与锚框面积成反比。对于每个边界框需要包含 6 个参数:(c,x,y,w,h) 和类别分布 {pc}c=1C,假设当前边界框对应锚框的宽和高分别为 (wa,ha) 其中
⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧c=Pr(Object)⋅IOUpredtrue,(x,y)=边界框中心坐标相对于当前网格的左上角,(w,h)=相对于当前网格下的锚框的宽高比例,pc=Pr(Class=c)
tricks:由于 c,x,y∈(0,1),w,h∈(0,∞),{pc}c=1C,则可以对模型的输出分别做 sigmoid(x),ex,softmax 变换。
标签处理
这部分将数据集的边界框标签转化为YOLOv3所需的标签,对于一个图片的全部真实边界框(目标框)集合,我们记为 T={bi=(cls,x,y,w,h):i∈{1,...,N}},其中 cls∈{1,...,C} 表示边界框对象的类别,(x,y) 表示边界框的中心点相对于整个图像的比例,(w,h) 表示边界框的宽高相对于整个图像的比例。
对于一个目标框 bt∈T,在网格划分 S 下,其中心点位于第 (i,j), i,j∈{0,...,S−1} 个网格处,易知
i=[xS],j=[yS],[⋅]表示取整函数
设锚框集合按照IOU从大到小排序记为
AS={b1,b2,⋯,b∣AS∣:IOUbubt>IOUbvbt,(u<v且u,v∈{1,⋯,∣AS∣})}
并且将排序后锚框 bi 对应于原锚框集合中的编号记为 ai,目标状态记为 yS∈RS×S×∣AS∣×6,其中 yS(i,j,k) 表示当前网格划分下第 (i,j) 个网格上的第 k 个锚框对应的六元组 (c,x,y,w,h,cls),分别表示置信度、边界框中心相对网格而坐标、边界框相对网格的宽高比例和所属的类别,给定样本忽略系数 αignore∈(0,1),则 bt 当且仅有以下 3 个状态之一:
-
正例(positive):b1 一定为正例,令置信度 ci,j,a1=1。
-
忽略样例(ignore):∀k∈{2,⋯,∣AS∣},若有 IOUbkbt>αignore,令置信度 ci,j,ak=−1。
-
负例(negative):既不是positive也不是ignore的锚框 ai,及 ∀i∈{2,⋯,∣AS∣},若有 IOUbibt⩽αignore,令置信度 ci,j,ak=0。
yS(i,j,ak)=⎩⎪⎪⎨⎪⎪⎧(1,x,y,w,h,cls),(−1,x,y,w,h,cls),(0,x,y,w,h,cls),k=1,IOUbkbt>αignore,IOUbkbt⩽αignore.
在损失中正例只对带有 1obj 的项产生损失,负例只对 1noobj 项产生损失,而忽略样例则不产生损失。损失的具体形式请见下一部分。
注意:上述的目标标签设置是基于“没有2个及以上的目标框的中心点处于同一网格内”,如果在数据集中出现该情况,则保留其中任意一个。
目标状态的空间维度:对于输入图像大小为 416×416×3 为例,输出的 S∈{13,26,52},则每个划分大小 S 下对应的 yS∈RS×S×∣AS∣×6,在构建数据集中最好要求标签保持矩阵形式,但是由于 S 的大小不一,所以考虑将前面的维度拉伸为 R(∑SS×S×∣AS∣)×6 就可以用矩阵进行保存了,使用时重新进行划分即可。
损失函数
设网格划分为 S,该划分下对应图像 x∈(0,1)416×416×3 的标签为 yS∈RS×S×∣AS∣×6, (S∈{13,26,52}),设模型的输出为(这里的 c^,x^,y^,w^,h^,{pc}c=1C 都已经过模型预测中提到的tricks处理)
(S,S,∣AS∣,5+C)={(c^,x^,y^,w^,h^,{pc}c=1C)ijk:(i,j,k)∈{1,⋯,S}2×{1,⋯,∣AS∣}}
则损失函数为:
L= i,j=1∑Sk=1∑A1ijnoobjλnoobj(−log(1+ec^ijk)) +1ijkobj[λcoordr∈{x,y}∑(−rlog(1+e−r^)−(1−r)log(1+er^)) +λcoordr∈{w,h}∑(rijkar^−r)2 +λobj(−IOUktrue(1+e−c^ijk)−(1−IOUkture)(1+ec^ijk)) +λclass(−log(softmax({pc})cij))]
这里第1,2,4项分别是对 cnoobj,(x,y)obj,cobj 损失的计算,由于预测结果都在 (0,1) 中间,所以使用的是BCE(Binary Cross-Entropy)损失;第3项是对 (w,h)obj 损失的计算,结果在 (0,∞) 中间,所以用MSE损失;最后一项是对 clsobj 损失的计算,是一个分布,所以用CE(Cross-Entropy)损失。
其中 rijka 表示在网格 (i,j) 处的第 k 个锚框对应的宽(r=w)高(r=h),λnoobj,λcoord,λobj,λclass 均为超参数,我取得分别为 2,2,1,1(论文中没有提到)。
训练结果
我在训练中使用了在ImageNet上训练的技巧,主要是Learning rate warming up和cosine anneal,看学习率曲线就能一眼看懂。有意思的是,当我冻结DarkNet部分时,训练结果极差,只有对全部参数进行训练时,才得到比较好的结果(估计还是先冻结在解冻训练效果才好些吧)。
我分别在PASCAL VOC和COCO数据集上进行了测试,都训练了80个epochs,PASCAL训练图像wandb-reports,COCO训练图像wandb-reports
由于没有进行数据增强,在PASCAL上的mAP@50只有64.9%低了10%,打算后续加入数据增强后再进行一次测试,模型权重也就先不上传了。
最后是视频识别效果GitHub - KataCV/yolov3/process_mp4.py,模型的识别速度447fps,剪辑速度为92fps(被视频读取速度所限制),上传了4个视频到Google Drive和百度网盘(提取码: 1234),都可以在线观看。


