第七周定义了第二型曲线积分(物理含义是变力做功)及其计算方法,Green 公式定义基本完成。
第二型曲线积分
设 AB−→ 为 n 维空间中的向量,则称它的单位向量为
AB→=∣AB−→∣AB−→
称 F:A⊂Rn→Rn 为向量场(类似于物理中的重力场,磁场)。
设 C⊂Rn 是光滑曲线,τ:C→Rn, ∣τ∣=1,τ(P) 为 C 在 P 处的单位切向量,则称 τ 为 C 的单位切向量场。
定义1(定向)
如果 τ 是 C 的连续的单位切向量场,则称 τ 是 C 的一个定向。
因为 C 上每一点的切向量都有两个方向,连续性要求不能两个相邻点方向是完全相反的,也就是说一个领域中的点都是指向一个方向的。
命题2(定向只有两个)
设 C⊂Rn 为光滑曲线,则 C 有且仅有两个定向。
思路: 使用 C 的参数表达式,构造出两个定向,注意定义域是否一样(一个是参数,一个是坐标),使用内积和函数的连续性证明唯二性。
证明:
-
存在性,设 α:[a,b]→C 为 C 的参数方程,则 C 有两个定向,分别是:τ=α′∘α−1,−τ。
-
唯二性,设 λ 也是 C 的定向,则 ∀P∈C,对两个定向 λ,τ 在 P 点处做内积,有
(λ⋅τ)(P)=±1则 λ⋅τ 也是连续的=======⇒由于 λ,τ 都是连续的λ⋅τ≡1 或 λ⋅τ≡−1
命题3(定向曲线)
设 τ 是 C 的一个定向,称 {C,τ} 是一个定向曲线。
简记为 C,C 是一个定向曲线,τ 为 C 的正向,如果是负向则记为 −C={C,−τ}。
定义4(第二型曲线积分)
设 C⊂Rn 为定向曲线,τ 为 C 的正向,设 F:C→Rn,
设 α:[a,b]→C 是 C 的参数方程,τ=α′∘α−1,方向为 α 参数增加的方向。
取 [a,b] 的一个分划 π:a=t0<t1<⋯<tN=b,考虑和式:
S=i=1∑NF(ξi)⋅τ(ξi)L(Ci)
其中 Ci=α([ti−1,ti]), ξi∈Ci。
如果存在 I∈R,使得 ∀ε>0,有 ∣I−S∣⩽ε,则称极限 Δπ→0limS 存在,且 Δπ→0limS=I。
如果 Δπ→0limS 存在,定义
∫CF⋅ds=Δπ→0limS
称为向量场 F 沿定向曲线 C 的积分。
定理5(性质及计算方法)
设 C⊂Rn 为定向曲线,τ 为 C 的正向,α:[a,b]→C 为 C 的参数方程,且 C 的正向是 α 参数增加的方向,设 F,G:C→Rn 连续,则
-
∫CF⋅ds=∫CF⋅τds(转化为第一型曲线积分)
-
∫CF⋅ds=∫abF(α(t))⋅α′(t)dt
-
设 k,l∈R,则 ∫C{kF+lG}⋅ds=k∫CF⋅ds+l∫CG⋅ds(线性性)
-
∫−CF⋅ds=−∫CF⋅ds
思路: ① 通过第一型曲线积分的和形式即可转化为第二型曲线积分的和形式。
② 通过 τ 的参数化表达式,转化为参数形式,转化为一维积分形式以后,利用一维积分的性质,③④ 就不难证明了。
证明: (就证明 ② 吧)
∫CF⋅ds=∫CF⋅τds=∫CF⋅(∣α′∣α′∘α−1)ds=∫abF(α(t))⋅∣α′∣α′(t)⋅∣α′(t)∣dt=∫abF(α(t))⋅α′(t)dt
对于 ds 的理解:
ds=τds=α′(t)dtτ:曲线切线方向,ds:弧长的微分位移=速度×时间
更加一般的,在具体的坐标系中计算第二型曲线积分:
设 OX 为直角坐标系,x=(x1,x2,⋯,xn),记 ds=(dx1,dx2,⋯,dxn)。
向量场 F=(F1(x),F2(x),⋯,Fn(x)),则
∫CF⋅ds=∫CF1(x)dx1+⋯+Fn(x)dxn
光滑曲线 C 的参数方程 α(t)=(x1(t),x2(t),⋯,xn(t))=x(t),则
∫CF1(x)dx1+⋯+Fn(x)dxn=∫abF(α(t))⋅α′(t)dt=∫ab(F1(x(t))x1′(t)+⋯+Fn(x(t))xn′(t))dt
从形式上看,就像是做了变量代换 dx1(t)=x1′(t)dt。
定义6(分段光滑曲线的第二型曲线积分)
设 C=i=1⋃NCi,Ci 为定向曲线,Ci 内部互不相交,F:C→Rn 连续,则
∫CF⋅ds=i=1∑n∫CiF⋅ds
C 分段光滑,设 α:[a,b]→C 为 C 的参数方程,设 F:C→Rn 连续,C=C1+C2+⋯+CN,且 Ci 的正向都是 α 的参数增加的方向,则
∫CF⋅ds=∫abF(α(t))⋅α′(t)dt
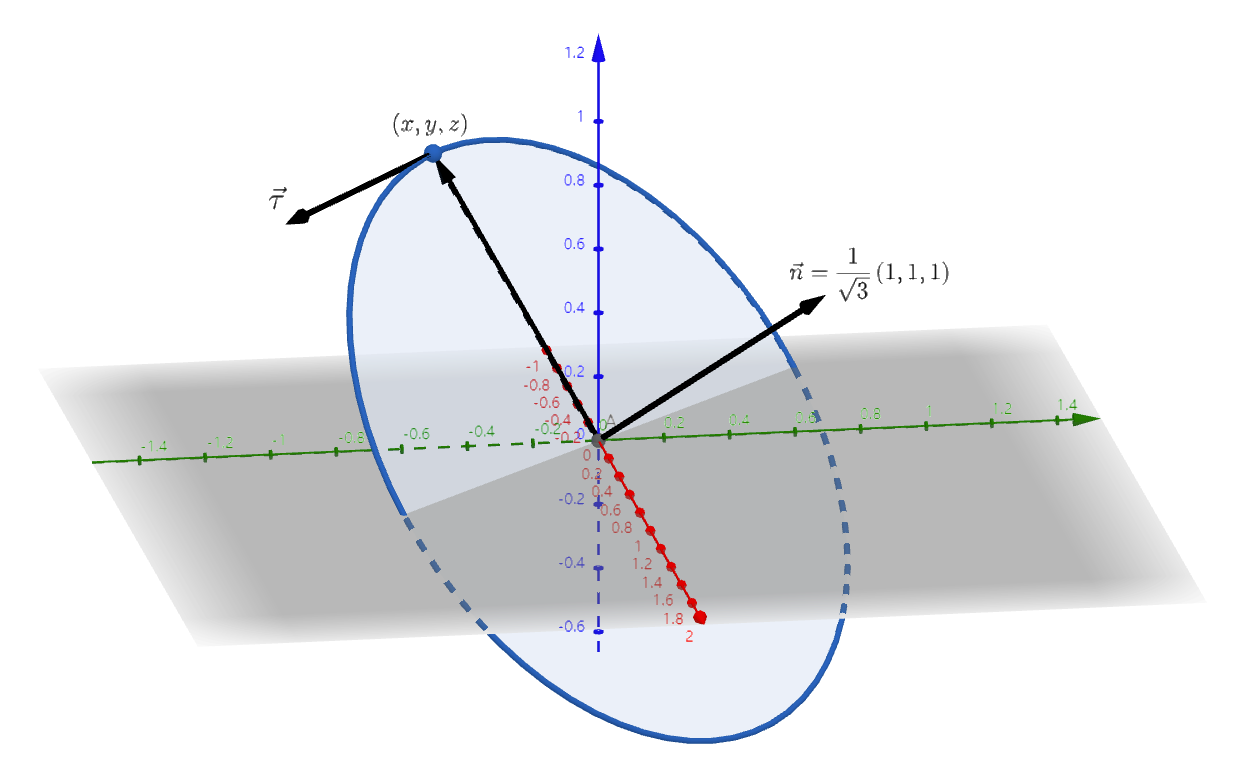
例一
Γ={(x,y,z)∈R3:x2+y2+z2=a2,x+y+z=0},Γ 的正向为逆时针方向。
求:(1). ∫Γxdx+ydy+zdz,(2). ∫Γzdx+xdy+ydz。
思路: 该题要结合图形解决,(1). (x,y,z) 和 τ 正交,所以 ∫Γ(x,y,z)⋅τdt=∫Γ0dt=0。
(2). 利用外积(叉乘)求出 τ=3a1(1,1,1)×(x,y,z),代入 ∫Γ(z,x,y)⋅τds,使用混合积和 xy+xz+yz=21((x+y+z)2−x2−y2−z2)=−2a2,即可计算出结果为 3πa2。
参考作图:
P.S. 这道题还有 Stokes 公式的做法,详见 Stokes 公式 - 例一。
Green公式
Green 公式能够将二维的第二型曲线积分(封闭曲线)转化为二重积分(由封闭曲线围成的区域),所以要能从封闭曲线围成的区域判断封闭曲线的定向,封闭曲线相当于区域的边界,判断方法是根据外法向来确定边界的定向(对外法向进行逆时针旋转),下面对这个过程进行详细定义。
定义1(某点处光滑,单位外法向量)
设 Ω⊂Rn 为开集,P∈∂Ω,如果 ∃P 的领域 U,
开集 D⊂Rn−1,f:D→R, f∈Ck, (1⩽k⩽+∞),使得在适当的坐标系下,
有 P=(x0,f(x0)), x0∈D,且
∂Ω∩UΩ∩U={(x,y):x∈D,y=f(x)}={(x,y):x∈D,y>f(x)}∩U
则称 ∂Ω 在 P 点为 Ck−光滑 (简称光滑),与 f 的光滑性一致。
在 x0 处的单位外法向量(也成单位外法向):n=1+∣∇f(x0)∣2(∇f(x0),−1),其中 ∇f(x0) 为 f 在 x0 处的梯度。
内法向量就是 n=1+∣∇f(x0)∣2(−∇f(x0),1),推导方法:
设 P=(x0,f(x0)),则在该坐标系下 P 点的切线方程为
l:0=f(x0)+▽f(x0)(x−x0)−y
取 (x1,y1),(x2,y2)∈l,则
0=0= f(x0)+▽f(x0)(x1−x0)−y1 f(x0)+▽f(x0)(x2−x0)−y2}⇒(▽f(x0),−1)⋅(x1−x2,y1−y2)=0
看最后一个变量,−1 则方向向下,是外法向,反之 (−▽f(x0),1) 则是内法向。
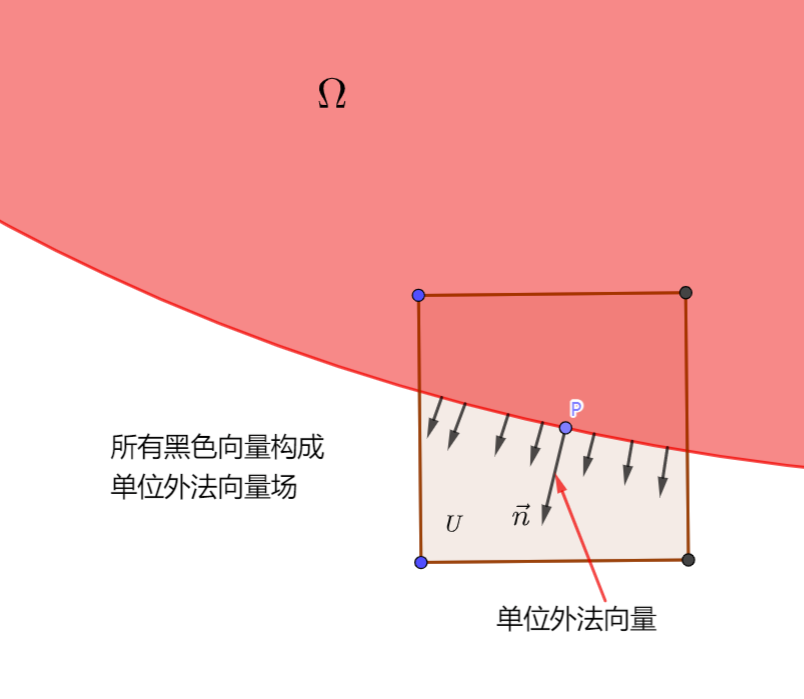
利用第一维的函数图像来刻画一个点附近的曲线图像,则该点的光滑性就可以用该函数的光滑性来表示。
定义2(平面分段光滑)
设 Ω⊂R2 为有界区域,∂Ω 为有限条内部互不相交的分段光滑的闭曲线,设 ∂Ω=i=1⋃NCi,Ci 满足:
-
Ci 为光滑曲线。
-
Ci 的内部 Ci∘ 互不相交。
-
∀p∈Ci∘,有 ∂Ω 在 P 点光滑。
则称 ∂Ω 分段光滑。
定义3(平面边界的单位内外法向量场,正向)
设 Ω⊂R2 为有界区域,∂Ω 分段光滑,∀P∈∂Ω,∂Ω 在 P 点光滑,则称 ∂Ω 光滑。
n=∂Ω→R2,n(P):=(n1(P),n2(P)) 为 ∂Ω 在 P 的单位外法向,称为 ∂Ω 的单位外法向(连续)。
设 Ω⊂R2 为有界区域,∂Ω 分段光滑,∂Ω=i=1⋃NCi。
设 τ 为 Ci 的一个定向,P∈Ci∘,则
τ(P)τ(P)=(−n2(P),n1(P)), τ=(−n2,n1), 逆时针=(n2(P),−n1(P)), τ=(n2,−n1), 顺时针
称 τ=(−n2,n1) 为 Ci 的正向。
定理4(Green公式)
设 Ω⊂R2 为有界区域,∂Ω 分段光滑,设 P,Q∈C1(Ωˉ),则
∫∂ΩPdx+Qdy=∫Ω{∂x∂Q−∂y∂P}dxdy
证明留到下个 note 了。

