卷积神经网络
简介
卷积神经网络(Convolution Neural Networks, CNN, ConvNet),结构特性:局部连接,权重共享,汇聚信息. 主要适用于图像处理的一种神经网络,其想法来源来自于生物模型中的感受野(Receptive Field),即视觉神经元只会接收到其所支配的刺激区域的信号,即获得某个区域内的加权平均结果,这种操作在数学中就是卷积.
卷积
这里的卷积指的是离散型的卷积形式.
一维卷积
设 {wi},{xi} 为两个数列,k∈R,定义 {wi} 与 {xi} 的有限卷积为以下数列
yt=k=1∑Kwkxt−k+1,(t⩾K)
其中 {wi} 称为滤波器(Filter)或卷积核(Convolution Kernel),{xi} 为信号序列,K 为滤波器长度.
如果我们将数列记为对应的函数值:w(i)=wi (1⩽i⩽K), x(i)=xi (1⩽i), y(t)=yt (K⩽t). 则上述定义可视为:数列 {wi},{xi} 在 R 上的零延拓,即 w(i)={wi,0,1⩽i⩽K,otherwise. 用更形象的方式将其列出如下
i=w(i)=x(i)=⋯,⋯,⋯,−1,0,0,0,w1,x1,1,w2,x2,2,w3,x3,⋯,⋯,⋯,K,wK,xK,K+1,0,xK+1,K+2,0,xK+2,⋯⋯⋯
定义两个离散数列 {wi},{xi} 的卷积如下:
w∗x:== i=−∞∑∞wixt−i+1i=t−j+1j=−∞∑∞xjwt−j+1=x∗w i=1∑Kwixt−i+1
通过 (3) 式可知卷积具有可交换性,(4) 式表明 (1) 式中定义的有限卷积其实就是在数列零延拓下的卷积,再截取 t⩾K 这一段的结果.
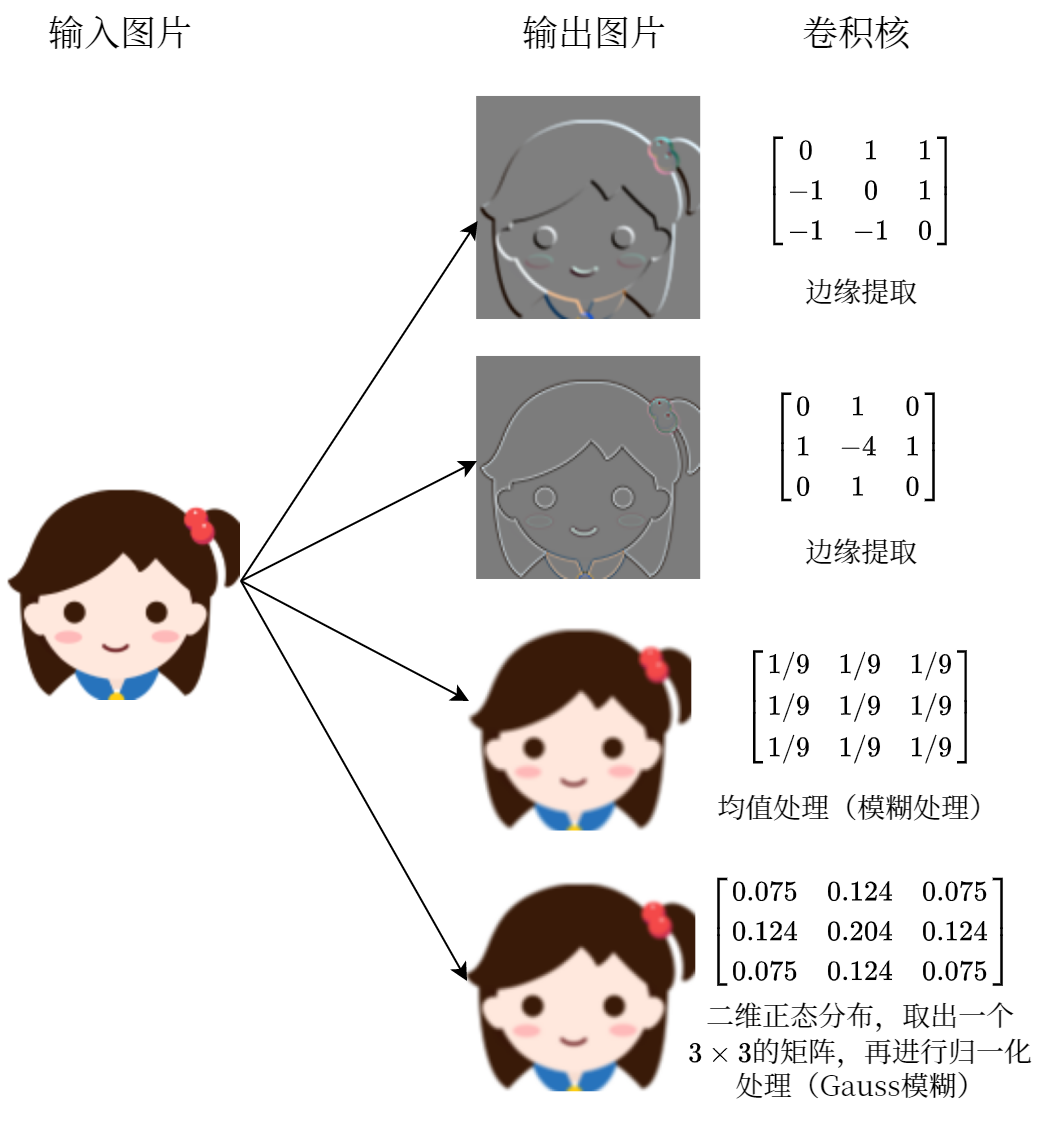
卷积操作在信号处理方面有不错的效果,可以通过不同的卷积核,对不同的信号进行提取. 下面是几个简单例子
-
简单移动平移:w=[1/k, 1/k, ⋯, 1/k](用于时间序列中消除数据的随机波动).
-
二阶微分近似:w=[1, −2, 1],由数值分析的知识可知,连续二阶可微函数 x(t),有如下近似式
x′′(t)≈h2x(t−h)−2x(t)+x(t+h)令h=1x(t−1)−2x(t)+x(t+1)
二维卷积
常用于图像处理,设图像 x∈RM×N ,卷积核 w∈RU×V,一般有 U≪M,V≪N,类比一维卷积定义,二维卷积定义如下:
yst=i=1∑Uj=1∑Vwijxs−i+1,t−j+1=i=−∞∑∞j=−∞∑∞wij′xs−i+1,t−j+1′=:w∗x
其中 wij′,xij′ 分别为 wij,xij 的零延拓,记 y=w∗x∈R. 下图是几种不同卷积核作用在一张图片上的效果:
互相关
在机器学习和图像处理中,卷积的作用主要是通过在一个图像上滑动一个卷积核,通过卷积操作得到一个新的图像. 在计算卷积过程中,需要对卷积核进行反转操作,即对卷积核旋转 π 大小. 这个操作就显得多余了,所以在计算机中经常将卷积视为互相关(Cross-Correlation)操作,即直接对卷积核和原图进行点积操作(对应位相乘).
设图像 x∈RM×N ,卷积核 w∈RU×V,则它们的互相关为:
yst=i=1∑Uj=1∑Vwijxs+i−1,t+j−1=i=−∞∑∞j=−∞∑∞wij′xs+i−1,t+j−1′=:w⊗x
和 (6) 式对照可知,互相关和卷积的区别仅仅在于卷积核是否需要翻转,即 w⊗x=rot(w)∗x,rot(w) 表示将矩阵 w 旋转 π 以后的结果. 因此互相关也称为不翻转卷积.
卷积的变种
在卷积的基础上,还可以引入步长和零填充增加卷积的多样性,以便更灵活地提取图像特征.
- 步长(Stride)指卷积核在滑动时的时间间隔.
- 零填充(Zero Padding)指对输入矩阵的边缘进行零填充.
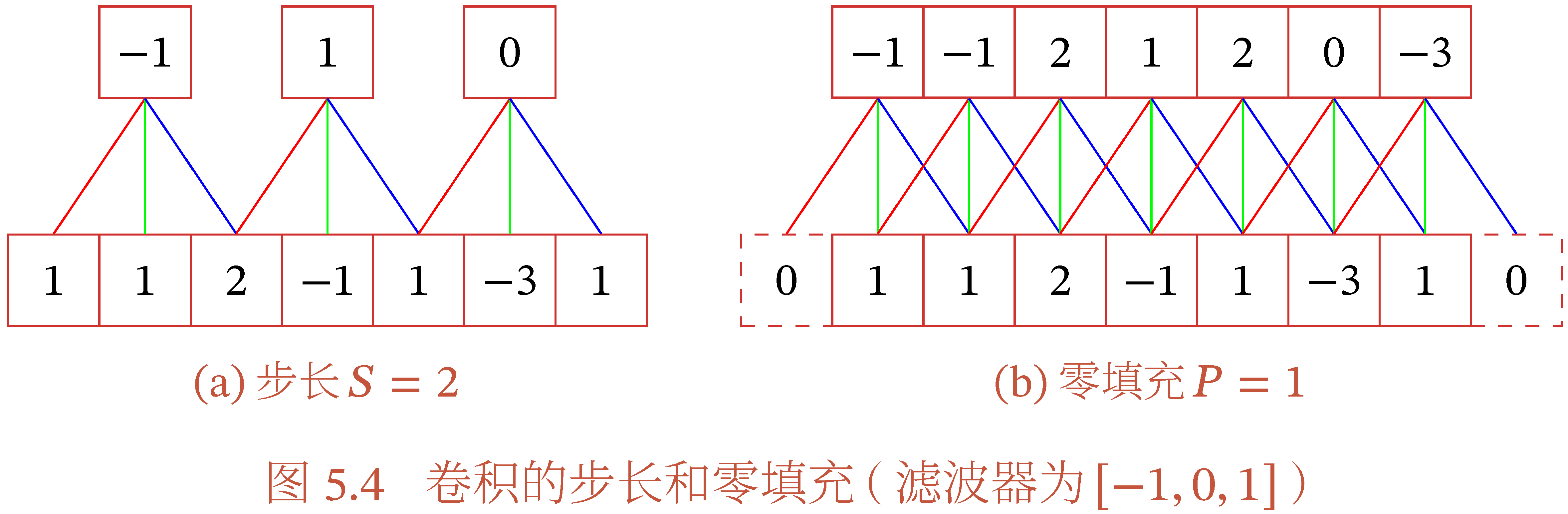
设卷积层的输入向量维数为 M,卷积大小为 K,步长为 S,在输入两端各填补 P 个 0,则输出向量维度为 (M−K+2P)/S+1,
常用卷积有以下三种:
- 窄卷积(Narrow Convolution):S=1,P=0,输出维度为 M−K+1.(普通卷积)
- 宽卷积(Wide Convolution): S=1,P=K−1,输出维度为 M+K−1.
- 等宽卷积(Equal-Width Convolution):S=1,P=(K−1)/2,输出维度为 K. 上图(b)就是一种等宽卷积.
卷积神经网络结构
卷积层
卷积层的作用是提取局部区域的特征,将输入卷积层的矩阵称为输入特征,将通过卷积层后的输出称为输出特征,也称特征映射(Feature Map).
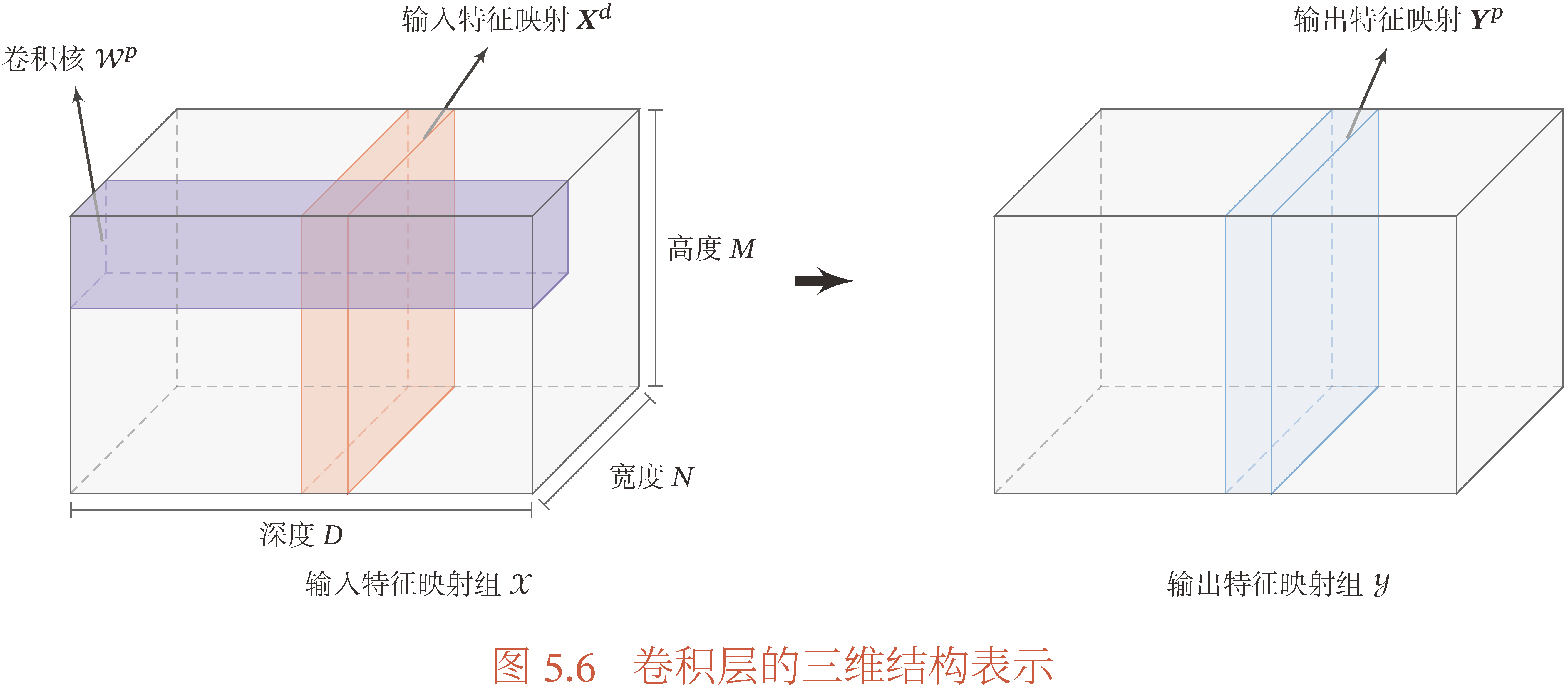
一般的图片每个像素由RGB三原色(颜色通道数为 3)构成,假设图片的宽度和高度分别为 N,M,颜色通道数为 D,则一张图片 x∈RN×M×D,由于图片的像素值一般为无符号 8 位整型,即 xijk∈[0,255],所以也有 x∈[0,255]N×M×D,当我们对图片进行归一化处理后,即 x←x/256,就有 x∈[0,1)N×M×D.
卷积层中,假设每个卷积核大小为 U×V,且每个颜色通道上都对应有 P 个卷积核,则卷积核 w∈RU×V×P×D,令第 d 个颜色通道上的第 p个卷积核为 wd,p. 由于每个卷积核 wd,p 作用在图片 x 上都会得到一个输出 yp,所以一共有 P 个输出特征,所以特征映射 y∈RN′×M′×P,N′×M′ 为卷积核 U×V 作用在 N×M 矩阵后的维度. 可以参考下图更好地理解.
汇聚层
汇聚层(Pooling Layer)也称池化层,子采样层(Subsampling Layer). 起作用是对卷积层输出的特征映射进一步进行特征选取,降低特征数量,减少参数数量.
设汇聚层的输入特征 x∈RN×M×D,对于其中每一个颜色通道中的图像 xd,划分为很多的区域 {Rijd},满足 ⋃ijRijd⊂{xij},这些区域可以是不交的,也可以有交集. 汇聚(Pooling)是指对每个区域进行下采样(Down Sampling)操作得到的值,作为该区域的概括.
常用的汇聚操作有以下两种:
-
最大汇聚(Maximum Pooling):对于一个区域 Rijd,选择这个区域内所有神经元的最大活性值作为这个区域的表示,即
yijd=x∈Rijdmaxx
-
平均汇聚(Mean Pooling):取该区域内的所有活性值的平均值作为该区域的表示,即
yijd=∣Rijd∣1x∈Rijd∑x
其中 ∣Rijd∣ 表示集合 Rijd 的基数,即该集合中所包含元素的个数.
卷积网络的一般结构
一个经典卷积网络由卷积层、汇聚层、全连接层堆叠而成,常用卷积神经网络结构如下图所示. 一个卷积块为一组连续 M 个卷积层和 b 个汇聚层构成(M 取值通常为 2∼5,且卷积核大小逐层增大,个数逐层增多,b 通常取为 0 或 1),卷积神经网络堆叠 N 个连续的卷积块,然后连接 K 个全连接层(N 通常取为 1∼100 或更大,K 一般取为 0∼2).
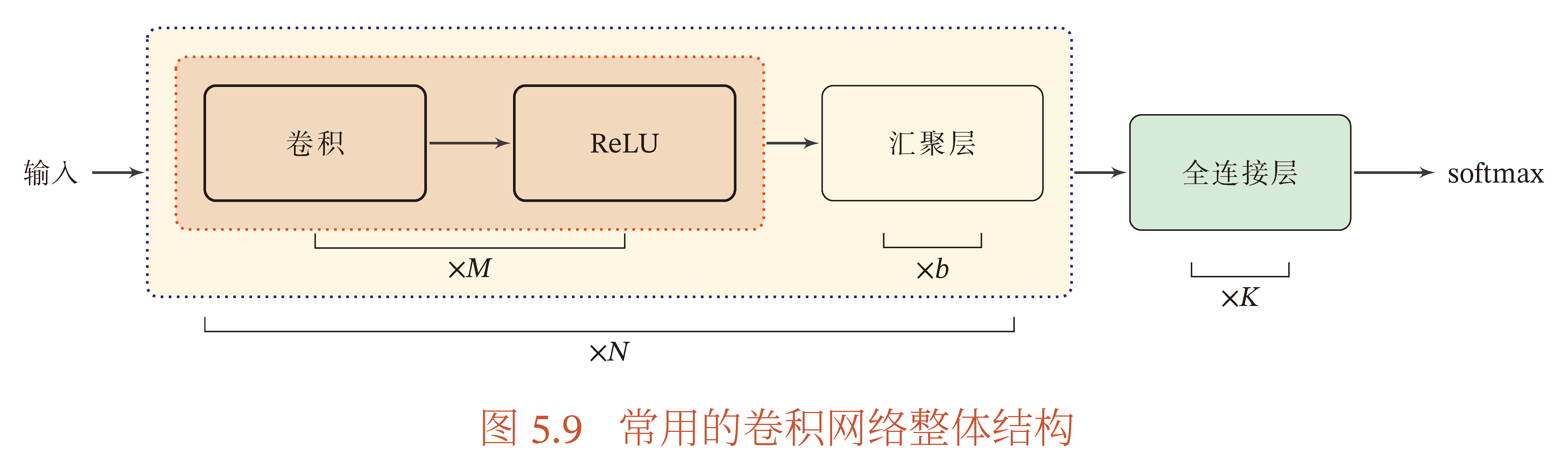
卷积网络的卷积核大小一般取为 2×2 或 3×3,以及更多的数量如 32 个或更多. 由于卷积可以设置步长减少输出特征的大小,所以汇聚层的作用并不显著了,可以通过增加步长来替代.
代码实现
完整代码:1. 基于前馈型全连接神经网络的数字识别;2. 基于RNN的数字识别(数据增强).
第一个版本是最简单的全连接神经网络模型,实现较为简单,对数据集的识别率已经达到 95% 以上,但是如果自定义输入数字,识别效果并不好. 所以第二个版本,在加入RNN的基础上,进行了数据增强操作.
数据增强简单来说就是对原有数据集的图像增加噪声,随机添加轻微扰动后再加入训练集,从而提高模型的鲁棒性. 常见的扰动操作有旋转,平移,拉伸,缩放等,下图就举出了一些例子,最左端为原始图片,右侧均为经过变换后的图片.
优化后的算法准确率达到 98% 甚至更高,而且对自定义数字输入识别率极高.

无监督学习
变分自动编码机
变分自动编码机(Variational AutoEncoder, VAE),是一种通过完全无监督的方式学习图片中的潜在特征编码.
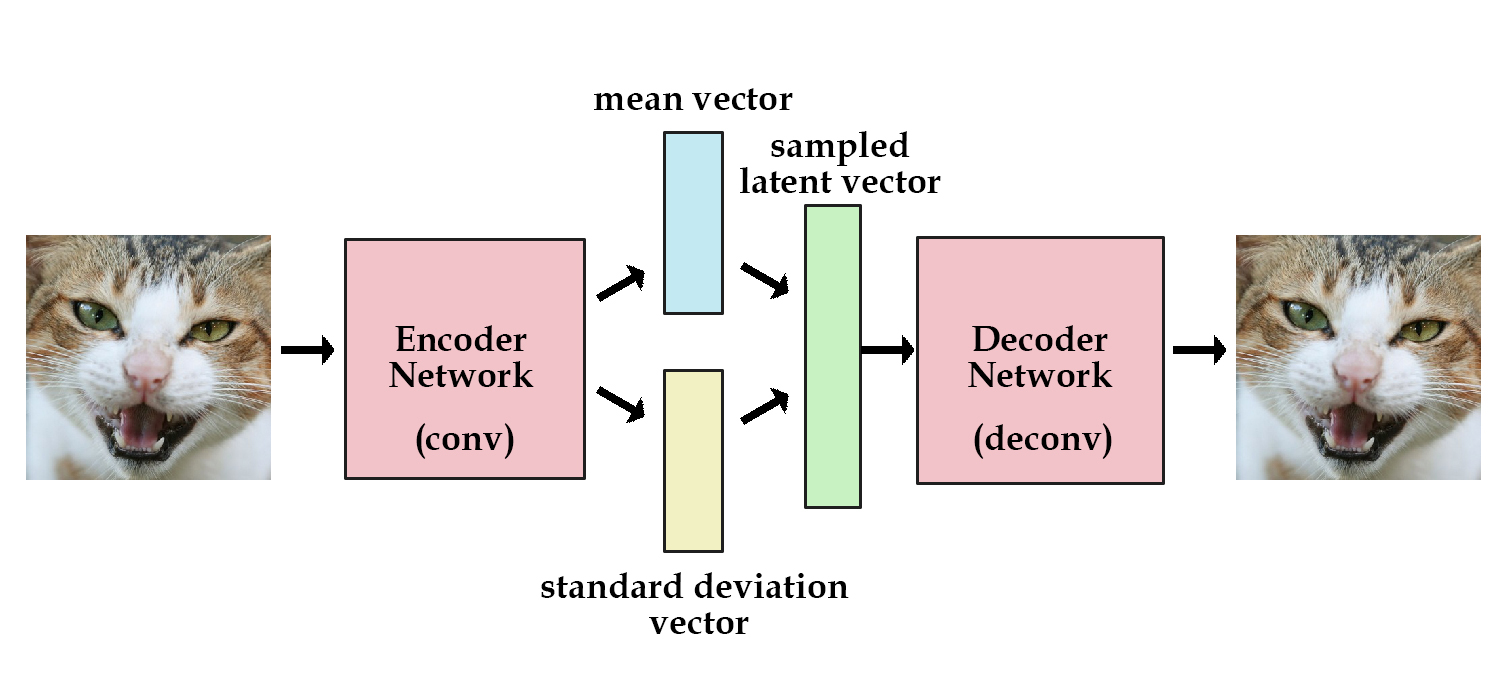
如上图和MIT 6.S191第四讲可知,VAE通过编码-解码(Encoder-Decoder)结构来学习输入数据的潜在表示. 在计算机视觉中,编码网络(Encoder Network)用于接受输入图像,将它们编码为一系列由均值 μ(Mean)和标准差 σ(Standard Deviation),通过这两个参数就可以定义出潜空间(Latent Space,概率分布函数,通常使用Gauss分布),然后从该空间中进行采样(Sample,根据概率分布随机取样),得到一组潜变量(Latent Variables). 然后通过解码网络(Decoder Network)对这些潜变量进行解码,从而得到输入图像的重建结果. 我们期望输出的结果与输入图像能够尽可能地相似.
设输入图像为 x,编码过程相当于计算出概率分布 qϕ(z∣x)(潜空间),然后对 qϕ(z∣x) 进行采样得到编码 z,然后对 z 进行解码计算出 x^,解码器也可以抽象为一个概率分布 pθ(x∣z). 我们期望输入图像与输出图像差别竟可能小,即 ∣∣x−x^∣∣2 尽可能小,且希望潜空间 qϕ(z∣x) 近似于某个期望的分布 p(z),即 D(qϕ(z∣x)∣∣p(z)) 最小,D(q∣∣p) 用于衡量两个概率分布的差距,一般取为KL散度.
在训练模型的过程中,可以通过VAE识别哪些潜变量对模型训练更加重要. 下面让我们将具体分析VAE的两个关键部分的损失函数,并讨论如何对其参数进行梯度更新.
VAE损失函数
潜空间就是潜变量的概率分布函数,可以通过在潜空间采样获得潜变量,我们需要将潜空间 N(μ,σ2I) 向一个标准Gauss分布 N(0,I) 近似,这样可以使得潜变量更具有连续性,避免其分布过于分散. 这里需要对可学习参数进行更新,所以我们需要定义第一个损失函数(Loss Function). 并且VAE用这些参数进行图像重建后,还需考虑和输入图像的匹配程度,这里需要第二个损失函数. 因此我们VAE的损失函数具有两项:
-
潜损失 Latent Loss LKL:用于衡量潜空间和标准Gauss分布的匹配程度,这里由 Kullback-Leibler (KL) 散度所定义.
-
重建损失 Reconstruction Loss Lx(x,x^):用于衡量重建所得到的图片与输入图片的匹配程度,由 L1 范数所定义.
潜损失的表达式(KL散度,μ,σ 分别为编码的均值和标准差):
LKL(μ,σ)=21j=0∑k−1(σj+μj2−1−logσj)
重建损失的表达式(L1 范数,其中 x 为输入特征,x^ 为重建输出):
Lx(x,x^)=∣∣x−x^∣∣1
综上,VAE损失为:
LVAE=c⋅LKL+Lx(x,x^)
其中 c 为潜损失的权系数,即用于正则化的加权系数.
重新参数化技巧
VAE需要使用“重新参数化技巧”(Reparameterization Trick)对潜变量取样,由于潜变量 z∼q(z∣x),而梯度下降法中不能出现随机变量,所以需要利用该技巧,将 z 固定下来. 由于 q(z∣x) 可由Gauss分布近似,则可以对 z 按照特定均值和方差的Gauss分布进行取样,从而可以进行梯度下降法对参数进行学习. 假设VAE编码中生成的均值和方差分别为 μ,σ,则潜变量 z∼N(μ,σ2I),可以通过多维标准正态分布 ε∼N(μ,I) 平移和等比放缩得到.
z=μ+e21log∑∘ε
其中 ∑=σ2I 为随机变量 z 的协方差矩阵.
去偏变分自动编码机
去偏变分自动编码机(Debiasing Variational AutoEncoder, DB-VAE)为VAE的一个增强版,在传统VAE基础上,它增加了去偏的功能:通过自适应重采样(自动选择数据,进行重复性训练)减轻训练集中的潜在偏差. 例如:面部识别训练集中,大多数图片的人脸都是正面图像,而侧脸的图像偏少,如果将它们均等地训练,训练出的模型可能对正脸识别效果优于侧脸的效果,这就是数据偏差(Debiasing). 为了平衡这种偏差有两种方法,一是使用人工处理,提高数据集中偏差数据的训练数量,但操作十分复杂,而且人无法判断哪些数据是偏差数据;二是通过机器自动识别偏差数据,然后自我调整数据的训练数量,这就是DB-VAE的提升之处. DB-VAE的示意图如下图所示,图片来源 Uncovering and Mitigating Algorithmic Bias through Learned Latent Structure.
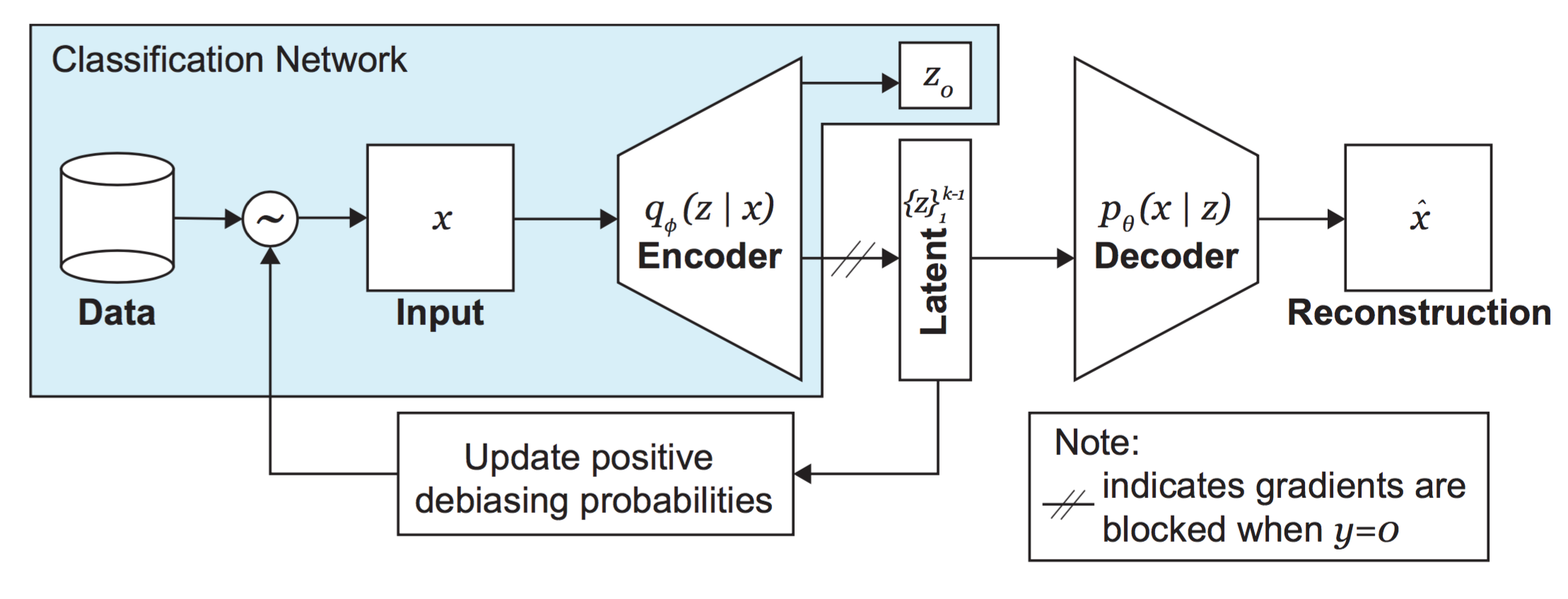
注意到,DB-VAE编码部分有一个单独输出的有监督变量 z0,例如,该变量可以用于判断是否该图片是人脸图像. 而一般的VAE并不具有有监督变量输出的功能,这也是DB-VAE与传统VAE不同之处.
需要注意如果是数据集中既有人脸图像也有非人脸图像,我们仅想学习人脸相关的潜变量,对数据集做去偏操作,并做一个二分类问题. 所以我们要确保模型仅对人脸图片从分布 qϕ(z∣x) 中获取无监督潜变量的表示,并且输出一个有监督的分类预测 z0,而对于非人脸图片,我们只需要输出一个预测 z0 即可.
DB-VAE损失函数
我们需要对DB-VAE的损失函数进行一些改进,损失函数要与是否是人脸图片相关.
对于人脸图片,我们的损失函数将包含两项:
-
传统VAE损失函数 LVAE:包含潜损失和重建损失.
-
分类损失 Ly(y,y^):二分类问题的标准交叉熵损失函数.
相反地,对于非人脸图片,我们的损失函数仅有分类损失这一项. 则DB-VAE损失函数为:
Ltotal=Ly(y,y^)+χimage(y)⋅LVAE
其中 χimage(y)={1,0,y=1,训练样本为人脸图片,y=0,训练样本为非人脸图片.
自适应重采样
回想DB-VAE的架构:当图像通过网络输入时,编码器会学习得到潜空间中 qϕ(z∣x) 的估计. 我们希望通过增加对潜空间中代表性不足区域的采样,从而增加稀有数据的相对训练次数. 我们可以通过每个学习到的潜变量的频率分布对 qϕ(z∣x) 进行近似,根据中心极限定理(随机变量部分和分布渐近与Gauss分布)近似结果应该趋近于Gauss分布,从该近似结果中我们可以得到出现每个潜变量的出现频率占比,然后将出现频率取倒数(提高出现频率低的样本的重采样率),再归一化处理,将这个概率分布将用于数据的重新采样.
代码实现
完整代码及解释 - Face Detection VAE.
目标为识别输入照片是否是人脸图像,我们使用了两个数据集:
-
正训练集:CelebA Dataset,包含超过二十万张名人照片.
-
负训练集:ImageNet,该网站上有非常多不同分类的图片,我们将从非人脸类别中选取负样本. 通过 Fitzpatrick度量法 对肤色进行分类,将图片标记为 “Lighter” 或 “Darker”.
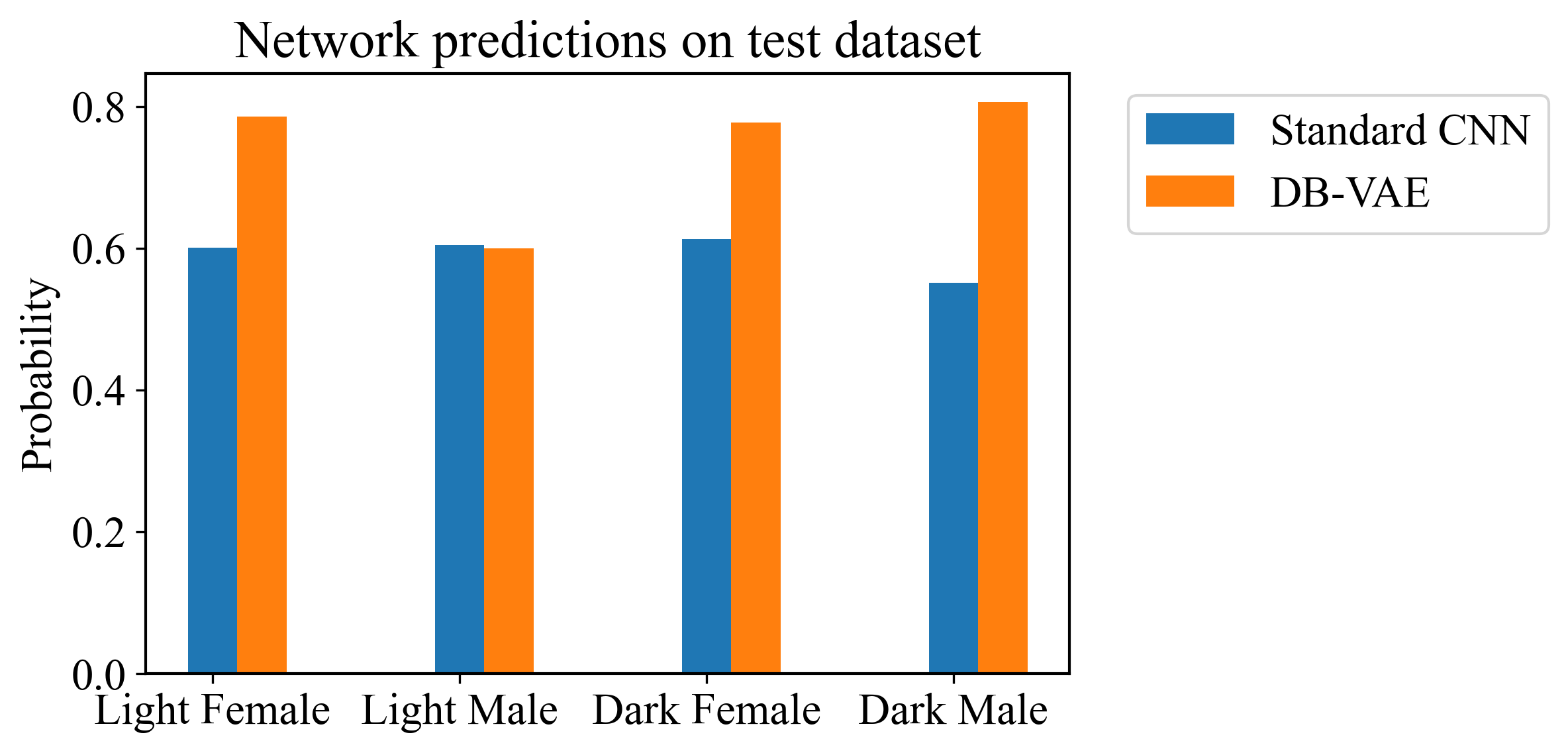
然后我们使用了经典CNN和DE-VAE神经网络对图片进行识别,下图体现出了去偏后的训练效果.
以下一些图片体现了VAE的图像渐变转化功能(变脸效果),清晰的图像为输入的图片(左右两端),较为模糊的图像为VAE输出的预测结果.