2017 Korea Daejeon Regional

官网地址

CF地址

补题，(和重做差不多了😂)

B - Connect3

题意

给出一个 $4\times4$ 的网格图，有两个玩家轮流下黑棋和白棋，每次下棋位置必须保证该棋子的下方有一个棋子，也就是堆栈，形式化地说就是，若下在 $(i, j)$ 处，当且仅当， $(i-1, j)$ 处必须有棋子。

若一个玩家获胜，规则类似于五子棋，只是将“五子”改成了“三子”，横着或竖着或斜着有三个同种颜色连着，执改棋玩家获胜。

黑棋先下，告诉你第一次下棋的位置和最后一个白棋下的位置，求最终一共有多少种棋盘(也就是不考虑过程，只考虑终态)。

思路

直接暴力模拟两个人的下棋顺序即可，总复杂度 $O(15^2\cdot16\cdot3)=10^6$ 。

注：判断胜利的方法和最终棋盘的状态(可以使用set<vector<vector<int>> > st)。

点击显/隐代码

#include <bits/stdc++.h>
#define db double
#define ll long long
#define int ll
#define vi vector<int>
#define vii vector<vi >
#define pii pair<int, int>
#define vp vector<pii >
#define vip vector<vp >
#define mkp make_pair
#define pb push_back
#define Case(x) cout << "Case #" << x << ": "
using namespace std;
const int INF = 0x3f3f3f3f;
const int MOD = 998244353;
int a, b, ans, num[5];
vii stk(6, vi(6, -1));
set<vii> used;
int dx[4] = {1, 0, 1, 1};
int dy[4] = {0, 1, -1, 1};
bool chk() {
	for (int i = 1; i <= 4; i++) {
		for (int j = 1; j <= 4; j++) {
			for (int k = 0; k < 4; k++) {
				int fg = 1;
				for (int t = 0; t < 3; t++) {
					int x = i + dx[k] * t, y = j + dy[k] * t;
					if (stk[x][y] == -1 || stk[x][y] != stk[i][j]) {
						fg = 0;
						break;
					}
				}
				if (fg) return 1;
			}
		}
	}
	return 0;
}
void dfs(int x, int y, int col) {
	if (stk[b][a] == 1) return;
	if (chk()) {
		if (x == a && y == b && col == 0 && used.count(stk) == 0) {
			used.insert(stk);
			ans++;
			//for (int i = 1; i <= 4; i++) {
			//	for (int j = 1; j <= 4; j++) {
			//		cout << stk[i][j] << ' ';
			//	}
			//	cout << '\n';
			//}
			//cout << '\n';
		}
		return;
	}
	for (int i = 1; i <= 4; i++) {
		if (num[i] < 4) {
			stk[i][++num[i]] = col ^ 1;
			dfs(num[i], i, col ^ 1);
			stk[i][num[i]--] = -1;
		}
	}
}
signed main(){
#ifdef _DEBUG
//	FILE *file = freopen("out", "w", stdout);
#endif
	ios::sync_with_stdio(0);
	cin.tie(0);
	int x;
	cin >> x >> a >> b;
	stk[x][++num[x]] = 1;
	dfs(1, x, 1);
	cout << ans << '\n';
	return 0;
}

E - How Many to Be Happy?

题意

给出一个含有N个节点M条边的带权值的无向图，对于其中的每一条边 $e$ ，定义 $H(e)$ 为将其加入到最小生成树中所需要删除掉的最少的边数。

求 $\sum_{e\in E} H(e)$ ， $E$ 为原图中的边集合。

$N \leqslant 100, M\leqslant 500$

思路

考虑 $Kruskal$ 算法过程，如果边 $e$ 要加入到最小生成树中，那么它所对应的两个端点必须不在同一集合中，于是问题转换为求解最小去掉多少边，从而将两个端点分离开，这就是标准的最小割，最小割转最大流就行了。

注：之前在图中的边一定是val值小于当前边，容量都为1的双向边。

点击显/隐代码

#include <bits/stdc++.h>
#define db double
#define ll long long
#define int ll
#define vi vector<int>
#define vii vector<vi >
#define pii pair<int, int>
#define vp vector<pii >
#define vip vector<vp >
#define mkp make_pair
#define pb push_back
#define Case(x) cout << "Case #" << x << ": "
using namespace std;
const int INF = 0x3f3f3f3f;
const int MOD = 998244353;
const int N = 100 + 10;
struct Dinic {
	struct Edge {
		int u, v, cap, flow;
	};
	vector<Edge> edges;
	vi G[N];
	int s, t, d[N], cur[N];
	void init(int n) {
		for (int i = 0; i < n; i++) G[i].clear();
		edges.clear();
	}
	void addedge(int u, int v, int cap) {
		edges.pb({u, v, cap, 0});
		edges.pb({v, u, 0, 0});
		G[u].pb(edges.size() - 2);
		G[u].pb(edges.size() - 1);
	}
	bool bfs() {
		memset(d, -1, sizeof(d));
		queue<int> q;
		q.push(s);
		d[s] = 0;
		while(!q.empty()) {
			int u = q.front();
			q.pop();
			for (int i : G[u]) {
				Edge &e = edges[i];
				if (d[e.v] == -1 && e.cap > e.flow) {
					d[e.v] = d[u] + 1;
					q.push(e.v);
				}
			}
		}
		return d[t] != -1;
	}
	int dfs(int u, int mx) {
		if (u == t || mx == 0) return mx;
		int sum = 0, f, sz = G[u].size();
		for (int &i = cur[u]; i < sz; i++) {
			Edge &e = edges[G[u][i]];
			if (d[e.v] == d[u] + 1 && (f = dfs(e.v, min(mx, e.cap - e.flow)))) {
				e.flow += f;
				edges[G[u][i] ^ 1].flow -= f;
				mx -= f;
				sum += f;
				if (mx == 0) break;
			}
		}
		return sum;
	}
	int calc(int s, int t) {
		this->s = s;
		this->t = t;
		int ret = 0;
		while (bfs()) {
			memset(cur, 0, sizeof(cur));
			ret += dfs(s, 9e18);
		}
		return ret;
	}
}dinic;
struct Node {
	int val, u, v;
	bool operator < (const Node &y) const &{
		return val < y.val;
	}
};
signed main(){
#ifdef _DEBUG
//	FILE *file = freopen("out", "w", stdout);
#endif
	ios::sync_with_stdio(0);
	cin.tie(0);
	int n, m;
	cin >> n >> m;
	vector<Node> a(m);
	for (int i = 0; i < m; i++) {
		cin >> a[i].u >> a[i].v >> a[i].val;
		a[i].u--, a[i].v--;
	}
	sort(a.begin(), a.end());
	int ans = 0;
	for (int i = 0; i < m; i++) {
		dinic.init(n);
		for (int j = 0; j < i; j++) {
			if (a[j].val < a[i].val) {
				dinic.addedge(a[j].u, a[j].v, 1);
				dinic.addedge(a[j].v, a[j].u, 1);
			}
		}
		ans += dinic.calc(a[i].u, a[i].v);
	}
	cout << ans << '\n';
	return 0;
}

F - Philosopher’s Walk

题意

给出一个 $N\times N$ 的图(类似于分形?)， $N=2^k(k\leqslant 15)$ ，图形是上一个图形通过对称和平移操作得到的，给出从起点 $(1,1)$ 出发的步数，求最后到达的位置。

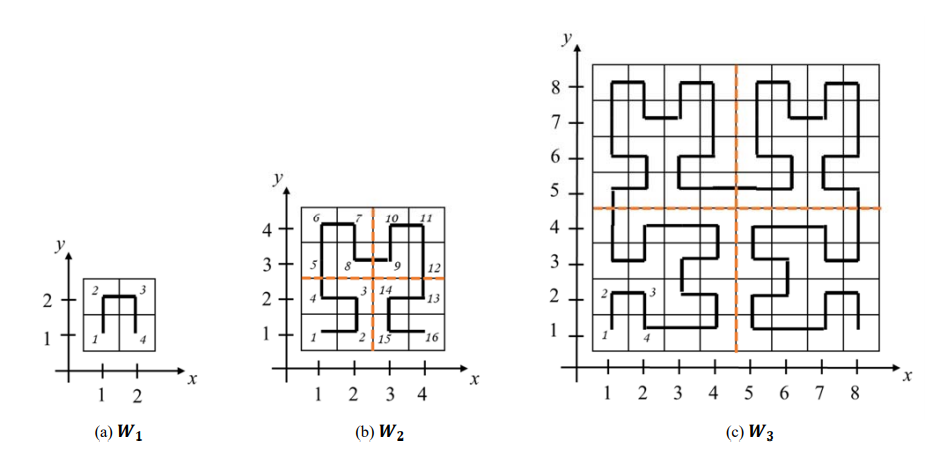
Figure F

思路

考试时好像写了半天，没有抓住题目的关键，就是图形的变换规律，将该图形分为四个区域：

左下是上一个图形关于x=y对称
左上是向上平移 $N/2$ 得到
右上是向右上平移 $N/2$ 得到
右下是先关于y=n/2-x对称后，再向右平移 $N/2$ 个单位后得到

使用递归即可，总复杂度 $O(K)$ 。

点击显/隐代码

#include <bits/stdc++.h>
#define db double
#define ll long long
#define int ll
#define vi vector<int>
#define vii vector<vi >
#define pii pair<int, int>
#define vp vector<pii >
#define vip vector<vp >
#define mkp make_pair
#define pb push_back
#define Case(x) cout << "Case #" << x << ": "
using namespace std;
const int INF = 0x3f3f3f3f;
const int P = 998244353;
pii dfs(int n, int num) {
	if (n ==  2) {
		if (num == 0) return mkp(1, 1);
		else if (num == 1) return mkp(1, 2);
		else if (num == 2) return mkp(2, 2);
		else return mkp(2, 1);
	}
	int tmp = num / (n * n / 4);
	pii ret = dfs(n/2, num % (n * n / 4));
	if (tmp == 0) {
		swap(ret.first, ret.second);
	} else if (tmp == 1) {
		ret.second += n/2;
	} else if (tmp == 2) {
		ret.first += n/2;
		ret.second += n/2;
	} else {
		int x = ret.first, y = ret.second;
		ret.first = n - y + 1;
		ret.second = n/2 - x + 1;
	}
	return ret;
}
signed main(){
#ifdef _DEBUG
//	FILE *file = freopen("out", "w", stdout);
#endif
	ios::sync_with_stdio(0);
	cin.tie(0);
	int n, m;
	cin >> n >> m;
	pii ans = dfs(n, m-1);
	cout << ans.first << ' ' << ans.second << '\n';
	return 0;
}

H - Rock Paper Scissors

题意

两个人玩石头剪刀布，给定对方的序列S和自己的序列T，将自己的序列放在S序列中的某处，使得自己能胜利最多，求最多胜利多少场？

##思路
对于三种获胜方式，也就是石头胜剪刀，剪刀胜布，布胜石头，分三类讨论，每次将自己序列胜利的设置为1其他为0，对方序列胜利的设置为1其他位0，于是做一次卷积即可求出每个位置，自己该状态获胜个数，最后三者求和，取最大值即可。

设 $A$ 为模式串长度为 $m$ ， $B$ 为文本串长度为 $n$ ， $A(x)$ 表示取出 $A$ 串中第 $x$ 个字符，设 $D(i) = A(m-i-1)$ ，则考虑一下函数：

\begin{aligned} f(x) &= \sum_{i=0}^{m-1}A(i)B(x-m+1+i)\\ &=\sum_{i=0}^{m-1}D(m-i-1)B(x-m+1+i)\\ &=\sum_{i=0}^{m-1}D(i)B(x-i) \end{aligned}

由于只有 $1\cdot 1=1$ 所以就能判断每个位置有多少该条件能获胜了。

时间复杂度 $O(3(n+m)\log (n+m))$ 。

点击显/隐代码

#include <bits/stdc++.h>
#define db double
#define ll long long
#define int ll
#define vi vector<int>
#define vii vector<vi >
#define pii pair<int, int>
#define vp vector<pii >
#define vip vector<vp >
#define mkp make_pair
#define pb push_back
#define Case(x) cout << "Case #" << x << ": "
using namespace std;
const int INF = 0x3f3f3f3f;
const int P = 998244353;
const int N = (1<<20) + 10;
int n, m, len, l;
int f[N], g[N], h[N], ans[N], rev[N];
char s[N], t[N];
void pre() {
	for (len = 1, l = 0; len <= n + m; len <<= 1, l++);
	for (int i = 0; i < len; i++) rev[i] = (rev[i>>1] >> 1) | ((i&1) << (l-1));
}
int ksm(int a, int b) {int ret = 1; while (b) {if (b & 1) ret = (ret * a) % P; a = a * a % P; b >>= 1;} return ret;}
void ntt(int *f, int fg) {
	for (int i = 0; i < len; i++) if (i < rev[i]) swap(f[i], f[rev[i]]);
	for (int i = 2; i <= len; i <<= 1) {
		int wn = ksm(3, (P-1) / i);
		if (fg == -1) wn = ksm(wn, P-2);
		for (int j = 0; j < len; j += i) {
			for (int k = j, w = 1; k < j + (i>>1); k++, w = w * wn % P) {
				int p = f[k], q = w * f[k+(i>>1)] % P;
				f[k] = (p + q) % P;
				f[k+(i>>1)] = (p - q + P) % P;
			}
		}
	}
	if (fg == -1) {
		int inv = ksm(len, P-2);
		for (int i = 0; i < len; i++) f[i] = f[i] * inv % P;
	}
}
void solve(char a, char b) {
	for (int i = 0; i < len; i++) {
		f[i] = (s[i] == a) ? 1 : 0;
		g[i] = (t[i] == b) ? 1 : 0;
	}
	ntt(f, 1), ntt(g, 1);
	for (int i = 0; i < len; i++) f[i] = f[i] * g[i] % P;
	ntt(f, -1);
	for (int i = 0; i < len; i++) ans[i] += f[i];
	//for (int i = 0; i < len; i++) ans[i] = (ans[i] + f[i] * g[i] % P) % P;
}
signed main(){
#ifdef _DEBUG
//	FILE *file = freopen("out", "w", stdout);
#endif
	ios::sync_with_stdio(0);
	cin.tie(0);
	cin >> n >> m >> s >> t;
	reverse(t, t + m);
	pre();
	solve('S', 'R');
	solve('R', 'P');
	solve('P', 'S');
	//ntt(ans, -1);
	int mx = 0;
	for (int i = m-1; i < len; i++) mx = max(mx, ans[i]);
	cout << mx << '\n';
	return 0;
}

I - Slot Machines

题意

给出 $n$ 个数字，你可以确定周期的开始位置 $k$ ，和从当前开始位置的周期 $p$ 使得原序列满足该条件（注：不要求最后一段完整），求 $k+p$ 的最小值。

思路

对kmp算法的精妙应用。

kmp算法是可以求出最小周期的，这道题如果能判断每个位置的最小周期，其实就能解决。

考虑将该数字序列反转，我们知道kmp可以求出当前后缀匹配的最长前缀长度，叫做border，假定当前位置为 $i$ ，当前位置的最长后缀记为 $border$ ，那么称 $i-border$ 就是满足上述条件的最小周期。

下面证明一下这个问题：

图一中，蓝色部分和红色部分字符串完全相同，那么我们称绿色部分就是当前位置 $i$ 向左的最小周期。

关键！图二中，可以看出绿色部分在蓝色部分中所占位置用紫色标出，那么由于蓝色和红色部分完全相等，那么该紫色部分就可以传递到红色部分上面。

于是以此类推，得出图三，紫色和绿色部分就是周期串，可以发现最左侧还差一点没有填满，那么它是什么呢？

用棕色标出来最后一段未填满部分，由于它在红色部分，又由于红色和蓝色相同，于是可以转移到蓝色上面，再对称下来，就正好是周期部分的一个前缀，这样最后一段就相当于是一个周期的前部分。

于是这样的周期就正好能够满足题意了。真的妙（

推广：如果我们要判断是否存在一个周期能完全填满以 $i$ 结束的前缀，
那么只需要保证 $i \bmod (i - border) = 0$ 就行了，这样就不存在最后棕色的那一小段了。

对于这道题，只需要将原串反过来，跑一次kmp，将每个位置的最优值求出来取 $\min$ 就行了。

时间复杂度 $O(n)$ 。

点击显/隐代码

#include <bits/stdc++.h>
#define db double
#define ll long long
#define vi vector<int>
#define vii vector<vi >
#define pii pair<int, int>
#define vp vector<pii >
#define vip vector<vp >
#define mkp make_pair
#define pb push_back
#define Case(x) cout << "Case #" << x << ": "
using namespace std;
const int INF = 0x3f3f3f3f;
const int P = 998244353;
void getfail(vi &s, vi &fail) {
	int n = s.size();
	for (int i = 1, j = 0; i < n; i++) {
		while (j && s[i] != s[j]) j = fail[j-1];
		if (s[i] == s[j]) fail[i] = ++j;
	}
}
signed main(){
#ifdef _DEBUG
//	FILE *file = freopen("out", "w", stdout);
#endif
	int n;
	cin >> n;
	vi s(n), fail(n);
	for (int i = n-1; i >= 0; i--) {
		cin >> s[i];
	}
	getfail(s, fail);
	int k = 1e9, p = 1e9;
	for (int i = 0; i < n; i++) {
		int nk = n - i - 1, np = i + 1 - fail[i];
		if (nk + np < k + p || (nk + np == k + p && np < p)) {
			k = nk;
			p = np;
		}
	}
	cout << k << ' ' << p << '\n';
	return 0;
}

K - Untangling Chain

题意

一个顶点再一个网格图上移动，一共移动 $N$ 步，给定每次移动的方向，请你确定每个方向上的移动距离，使得最终的移动路径不会有交点。

$N\leqslant 10^4$

思路

维护一个当前最小矩形覆盖，也就是可以通过这个矩形覆盖当前走过的所有路径，然后每次移动只要都恰好移动出该矩形，即可保证下一次转向的方向上，除了当前顶点外，没有其他路径。

总复杂度 $O(N)$

点击显/隐代码

#include <bits/stdc++.h>
#define db double
#define ll long long
#define int ll
#define vi vector<int>
#define vii vector<vi >
#define pii pair<int, int>
#define vp vector<pii >
#define vip vector<vp >
#define mkp make_pair
#define pb push_back
#define Case(x) cout << "Case #" << x << ": "
using namespace std;
const int INF = 0x3f3f3f3f;
const int P = 998244353;
signed main(){
#ifdef _DEBUG
//	FILE *file = freopen("out", "w", stdout);
#endif
	ios::sync_with_stdio(0);
	cin.tie(0);
	int n, dir = 0, x = 0, y = 0, mxx = 0, mnx = 0, mxy = 0, mny = 0;
	cin >> n;
	for (int i = 0; i < n; i++) {
		int a, b;
		cin >> a >> b;
		if (dir == 0) {
			cout << mxx - x + 1 << ' ';
			x = ++mxx;
		} else if (dir == 1) {
			cout << mxy - y + 1 << ' ';
			y = ++mxy;
		} else if (dir == 2) {
			cout << x - mnx + 1 << ' ';
			x = --mnx;
		} else {
			cout << y - mny + 1 << ' ';
			y = --mny;
		}
		dir = (dir + b + 4) % 4;
	}
	return 0;
}

coding > ICPC

#暴力 #网络流 #最小割 #Kruskal #递归 #FFT #字符串

2017 Korea Daejeon Regional

https://wty-yy.github.io/posts/56269/

作者

wty

发布于

2021年8月14日

许可协议

ABC214 上一篇

原根的性质及运用下一篇