多元函数的 Riemann积分 Darboux积分 Lebesgue外侧度

数学分析第一周，讲了多元函数关于 $Riemann$ 积分的定义和 $Darboux$ 积分的等价证明，定义了 $Lebesgue$ 外侧度及其一些性质。

多元函数的 $Riemann$ 积分的定义，总体思路和一元函数的定义类似，通过定义多元空间中的一个分划，然后定义出 $Riemann$ 和，且在分划足够细的时候，$Riemann$ 和会趋近于一个常数 $I$，这个 $I$ 就是 $f$ 在 $Q$ 上的 $Riemann$ 积分值。

于是先定义下前置芝士：

前置定义

闭方体：$\displaystyle Q=\prod_{i=1}^n[a_i,b_i],\ -\infty < a_i < b_i < +\infty$。

直径：$\text{diam}Q = \sqrt{\sum_i(b_i-a_i)^2}$。

“体积”（在三维的时候叫体积，二维叫面积）：$V(Q)=\prod_i\mid b_i-a_i\mid$。

分划：

• 先定义第 $i$ 维区间 $[a_i,b_i]$ 上的分划： $a_i=c_i^0 < c_i^1 < \cdots < c_i^{N_i} = b_i$，$(1\leqslant i\leqslant n)$
• $n$ 维空间 $Q$ 的分划：$\displaystyle\pi = \{\prod_{i=1}^n[c_i^{j_i-1}, c_i^{j_i}]:1\leqslant j_i\leqslant N_i, 1\leqslant i\leqslant n\}$

分划程度：$\Delta\pi=\max\limits_{q\in\pi}\text{diam}(q)$

分划的细分：对于 $Q$ 的两个分划 $\pi_1, \pi_2$，若 $\forall q\in\pi_2, \exists p\in\pi_1$，使得 $q\subset p$，则称 $\pi_2$ 是 $\pi_1$ 的一个细分，记为 $\pi_2\geqslant \pi_1$。

立方体的中心：若 $\displaystyle q=\prod_{i}[a_i,b_i]$，则 $q$ 的中心 $c_q=\left(\frac{a_i+b_i}{2}\right)^n_{i=1}$

以中心放缩：设 $r > 0$，则 $q$ 以中心放缩 $r$ 倍为：$rq:=\{r(x-c)+c:x\in q\}$

Riemann多元积分

定义1 （闭方体上的Riemann积分）

$Q\subset \mathbb R^n$ 为闭方体，$f:Q\rightarrow \mathbb{R}$，设 $\pi$ 是 $Q$ 的一个分划，考虑和式：

$$S=\sum_{q\in\pi}f(\xi_q)V(q)$$

其中 $\xi_q\in q$（具有任意性），将 $S$ 称为 $f$ 相应于 $\pi$ 的 $Riemann$ 和。

设 $I\in\mathbb R$，若 $\forall \varepsilon > 0, \exists \delta > 0$，使得当 $\Delta\pi\leqslant \delta$ 时，有 $\mid S-I\mid \leqslant \varepsilon$，

则称 $\lim\limits_{\Delta\pi\rightarrow 0} S$ 存在，记 $\lim\limits_{\Delta\pi\rightarrow 0}S=I$。

如果 $\lim\limits_{\Delta\pi\rightarrow 0}S$ 存在，称 $f\ Riemann$ 可积，记 $\int_Q f(x)\,dx = \lim\limits_{\Delta\pi\rightarrow 0}S$，可以简记为 $\int_Q f$。

注：这里的 $x$ 其实都应该是 $n$ 维向量 $\vec{x}$，由于老师也没写（偷懒bushi）就都默认是向量了，下文中出现的 $x$ 也基本都是 $n$ 维向量。

不难发现，常值函数 $f(x)=C$ 的在 $Q$ 上的 $Riemann$ 积分就是 $\int_Q f=C\cdot V(Q)$，特别的，如果令 $C=1$，积出来的就是 $Q$ 的“体积” $V(Q)$。

命题2 （可积固然有界）

如果 $f\ Riemann$ 可积，则 $f$ 有界。

思路：先随便取一个分划 $\pi$，对于 $Q$ 中任意一个向量，一定属于 $\pi$ 的某一个闭方体中，将其取出，利用 $Riemann$ 可积定义构造不等式即可，下面略证。

证明：

有 $Riemann$ 可积性知：$\displaystyle \left|\sum_{q\in\pi}f(\xi_q)V(q)-I\right|\leqslant 1$，

对于 $\forall x\in Q$，$\exists p\in\pi$，使得 $x\in p$，并设 $c_q$ 为 $q$ 的中心，则有：

$$\begin{aligned} &\left|f(x)V(p)+\sum_{q\in\pi,q\neq p}f(c_q)V(q)-I\right|\leqslant 1\\ \Rightarrow&|f(x)|\cdot V(p)\leqslant \sum_{q\in\pi}|f(c_q)|V(q)+|I|+1,\ \text{令} m=\min\limits_{q\in\pi}V(q)\\ \Rightarrow&|f(x)|\leqslant \left(\sum_{q\in\pi}|f(c_q)|V(q)+|I|+1\right)/m \end{aligned}$$

右式中和左侧的 $x$ 无任何关系，故 $f$ 在 $Q$ 上有界。

（引入中心点 $c_q$ 也是为了使得右式为一个只和 $\pi$ 相关的常数）

QED

Darboux多元积分

设 $f:Q\rightarrow \mathbb{R}$ 有界，$A\subset Q$， 先引入三个定义：

• $m_A=\inf\limits_{a\in A}f(a)=\inf\limits_A f$
• $M_A=\sup\limits_{a\in A}f(a)=\sup\limits_A f$
• $w_A=M_A-m_A$ ， $f$ 在 $A$ 上的振幅

定义3 （Darboux上下和）

设 $\pi$ 是 $Q$ 的一个分划，则：

• Darboux下和：$\underline{S}(\pi) = \sum\limits_{q\in\pi}m_qV(q)$
• Darboux上和：$\overline{S}(\pi) = \sum\limits_{q\in\pi}M_qV(q)$

命题4 （与Darboux上下和有关的不等式）

1. 设 $Q$ 的两个分划 $\pi_1,\pi_2$，满足 $\pi_2\geqslant \pi_1$，则 $\overline{S}(\pi_2)\leqslant \overline{S}(\pi_1), \underline{S}(\pi_2)\geqslant \underline{S}(\pi_1)$。

思路：通过细分的性质，将属于同一个 $p$ 的 $q$ 统一计数，再通过 $m_A$ 的定义即可。

2. 对于任意两个 $Q$ 的分划 $\pi_1,\pi_2$，有 $\underline{S}(\pi_1)\leqslant\overline{S}(\pi_2)$。

思路：引入一个 $\pi$，满足 $\pi\leqslant \pi_1$ 且 $\pi\leqslant\pi_2$，再使用上面刚证明的不等式即可。

定义5 （Darboux上下积分）

对于任意的 $Q$ 的分划 $\pi$：

• Darboux下积分：$\underline{\int}_Q f = \sup\limits_\pi \underline{S}(\pi) = \sup\limits_\pi\left(\sum\limits_{q\in\pi}\left(\inf\limits_qf\right)V(q)\right)$

• Darboux上积分：$\overline{\int}_Q f = \inf\limits_\pi \overline{S}(\pi) = \inf\limits_\pi\left(\sum\limits_{q\in\pi}\left(\sup\limits_qf\right)V(q)\right)$

则有：$\underline{\int}_Qf\leqslant\overline{\int}_Qf$

定义6 （Darboux可积）

若 $\underline{\int}_Qf = \overline{\int}_Qf$，则称 $f\ Darboux$ 可积，并称 $\underline{\int}_Qf$ 为 $f$ 的 $Darboux$ 积分。

定理7 （Riemann可积$\iff$Darboux可积）

设 $Q\subset \mathbb{R}^n$ 为闭方体，$f:Q\rightarrow \mathbb{R}$ 有界，则下列命题等价：

1. $f\ Riemann$ 可积。

2. $f\ Darboux$ 可积。

3. $\forall \varepsilon > 0$，存在 $Q$ 的一个分划 $\pi$，使得 $\sum\limits_{q\in\pi}w_qV(q)\leqslant\varepsilon$。

4. $\forall \varepsilon > 0, \exists \delta > 0$，使得对于 $Q$ 的满足 $\Delta\pi \leqslant \delta$ 的分划 $\pi$ 都有：$\sum\limits_{q\in\pi}w_qV(q)\leqslant \varepsilon$。

思路：分别考虑四个证明：

$①\Rightarrow ②:$ 通过 $Riemann$ 可积的定义，写出 $\varepsilon$ 语言，然后将 $Darboux$ 上下和限制在 $\varepsilon$ 范围内即可。

$②\Rightarrow ③:$ 通过 $Darboux$ 上下积分的定义，取两个分划，分别写出 $\varepsilon$ 语言，然后取一个比两个都更细的分划，最后该分划可以被夹在 $\varepsilon$ 范围内即可。

$④\Rightarrow ①:$ 基本和 $Riemann$ 积分定义相同，通过 $Darboux$ 上下和对 $Riemann$ 和进行限制，从而证明 $Riemann$ 和收敛。

$③\Rightarrow ④:$ 证明最为复杂，需要先引入两个引理：

引理1：设 $K\subset \mathbb{R}^n$ 为非空紧集，$\Omega \subsetneqq \mathbb{R}^n$ 为开集， $K\subset \Omega$，则：

$$\text{dist}(K, \partial \Omega):=\inf\limits_{x\in K, y\in\partial\Omega} |x-y| > 0$$

思路：对紧集 $K$ 使用有限覆盖定理，有限覆盖定理可以将一个紧集（可能有无限个元素）拆分成有限个“点”（很小的开集）组成，于是考虑每个“点”的一个半径为 $r_i$ 的球邻域包含于 $\Omega$，那么就有：

$$\text{dist}(K, \partial \Omega) > \min\limits_{i}(r_i) > 0$$

引理2：设 $P_i, (1\leqslant i\leqslant m)$ 为闭方体，$Q_j, (1\leqslant j\leqslant l)$ 为闭方体，且 $Q_j^{\circ}$ 互不相交，若

$$\bigcup_{j}Q_j\subset\bigcup_{i}P_i$$

则有

$$\sum_iV(P_i)\geqslant \sum_jV(Q_j)$$

思路：如果 $\bigcup\limits_{j}Q_j=\bigcup\limits_{i}P_i$，那么 $\{Q_j\}$ 就是 $\bigcup\limits_{i}P_i$ 的一个分划，如果 $\bigcup_{j}Q_j\subsetneqq\bigcup_{i}P_i$，那么可以找到一个区域不包含于 $Q$ 但包含于 $P$，且这个区域是一个开集“体积”不为0。

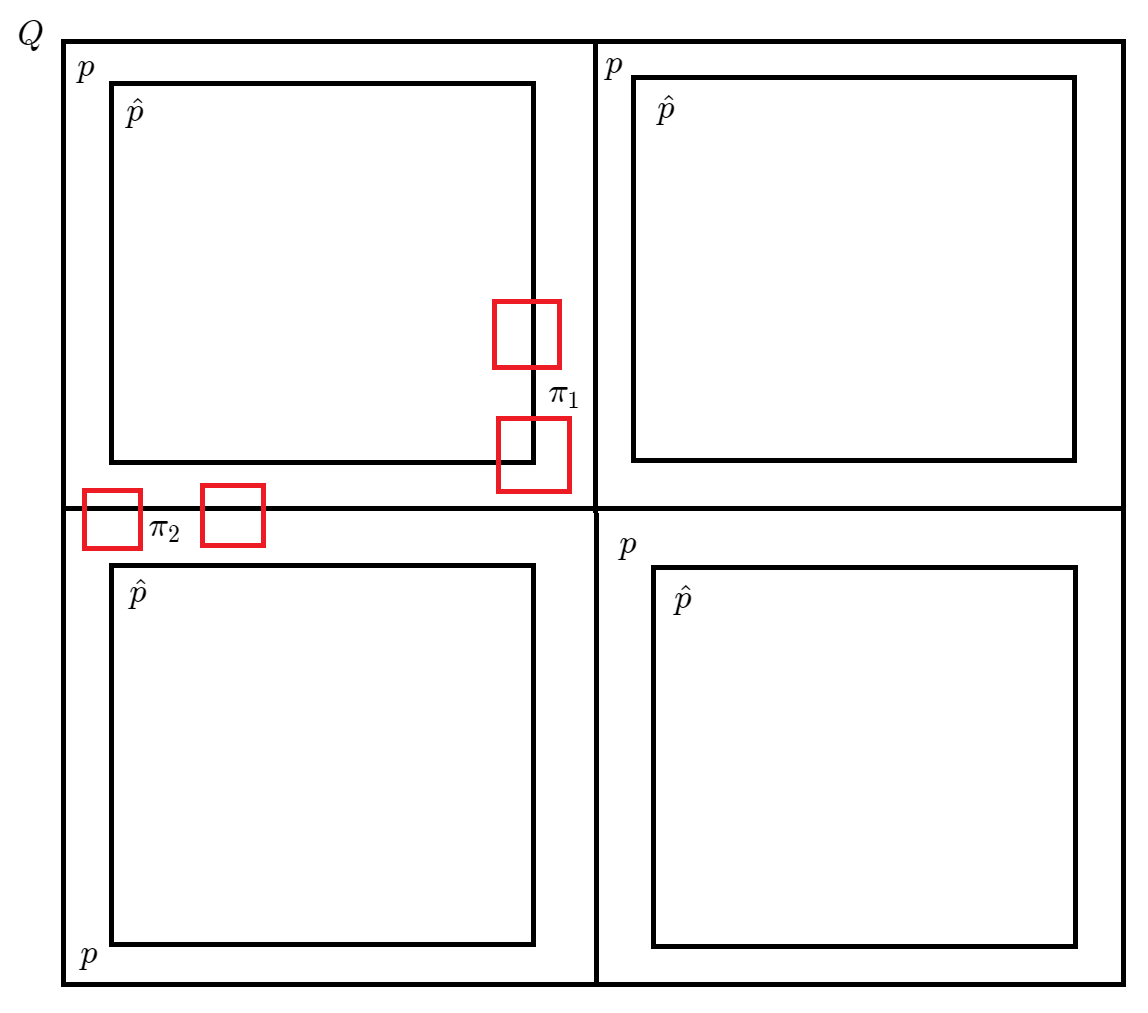
原命题证明的大致思路：随便给出一个满足条件 $3$ 的分划，然后对于每个子集缩小 $(1-\varepsilon)$ 倍，然后验证每个 $\Delta\pi\leqslant \min\limits_p \text{dist}((1-\varepsilon)p, \partial p)/2$ 的分划都能满足条件 $4$。

$③\Rightarrow ④$ 证明：设 $0 < \varepsilon < 1$，则存在 $Q$ 的分划 $\alpha$，使 $\sum\limits_{p\in\alpha}w_pV(p)\leqslant\varepsilon$，

设 $p\in\alpha$，记 $\hat{p} = (1- \varepsilon) p$（这里就是将 $p$ 以中心缩小 $(1-\varepsilon)$ 倍，严格定义见 前置定义），

则 $\hat{p}\subset p^\circ$，由引理1知：$\text{dist}(\hat{p}, \partial p) > 0$，

取 $\delta = \min\limits_{p\in\alpha} \text{dist}(\hat{p}, \partial p) / 2$。（下面就是验证的过程了）

设 $\pi$ 满足 $\Delta\pi\leqslant \delta$，只需证 $\sum\limits_{q\in\pi} w_qV(q)\leqslant C\cdot \varepsilon$，接下来将 $\pi$ 中的集合分为两种，一种是和 $\hat{p}$ 相交的 $\pi_1$，一种是不相交的 $\pi_2$。（这样更加细分后有妙用，只需分别证明 $\pi_1,\pi_2$ 都能被 $\varepsilon$ 限制住就行了）

• $\pi_1 = \{q\in\pi:\exists p_0\in \alpha, q\cap\hat{p_0}\neq \varnothing\}$

• $\pi_2 = \{q\in\pi:\forall p\in\alpha, q\cap\hat{p} = \varnothing\}$

则 $\pi = \pi_1+\pi_2$，于是 $\displaystyle \sum_{q\in\pi}w_qV(q)=\sum_{q\in\pi_1}w_qV(q)+\sum_{q\in\pi_2}w_qV(q)$

分为两部分解决：

$\pi_1$：先证明 $\pi_1$ 中的每一个元素都一定在某个 $p$ 当中（因为 $\Delta\pi$ 的限制给的很足）

设 $q\in\pi_1, \exists p\in\alpha$ 使 $\hat{p}\cap q\neq \varnothing$，又 $\text{dist}(\hat{p}, \partial p)\geqslant 2\delta$ 且 $\text{diam } q\leqslant \delta$，故 $q\subset p$。

对 $\pi_1$ 进行进一步的划分：令 $\pi_{1, p} = \{q\in\pi_1: q\subset p\}, p\in\alpha$，

当 $p_1\neq p_2$ 时，$\pi_{1,p_1}\cap\pi_{1,p_2} = \varnothing$，则 $\pi_1=\sum\limits_{p\in\alpha}\pi_{1, p}$（这里的 $\sum$ 是集合的不交并）。

于是有（第二个不等号处使用了引理2）：

$$\sum_{q\in\pi_1}w_qV(q)=\sum_{p\in\alpha}\sum_{q\in{\pi_{1, p}}} w_qV(q)\leqslant \sum_{p\in\alpha}w_p\sum_{q\in\pi_{1,p}}V(q)\leqslant \sum_{p\in\alpha}w_pV(p)\leqslant \varepsilon$$

下面证明 $\pi_2$ 的部分：

$f$ 有界，设 $|f|\leqslant M$（$f$ 的上界为 $M$），则 $\displaystyle \sum_{q\in\pi_2}w_qV(q)\leqslant 2M\sum_{q\in\pi_2}V(q)$

由于 $\displaystyle V(Q) = \sum_{q\in\pi_1} V(q) +\sum_{q\in\pi_2} V(q), \bigcup_{p\in\alpha} \hat{p}\subset\bigcup_{q\in\pi_1}q$，

则 $\displaystyle \sum_{q\in\pi_1}V(q)\geqslant \sum_{p\in\alpha}V(\hat{p}) = (1-\varepsilon)^n\cdot V(Q)$，

故（第二个不等号使用Bernoulli不等式）：

$$\sum_{q\in\pi_2}w_qV(q)\leqslant 2M(1-(1-\varepsilon)^n)V(Q)\leqslant 2MnV(Q)\varepsilon\leqslant C\cdot \varepsilon$$

综上：$\sum\limits_{q\in\pi}w_qV(q)\leqslant (C+1)\varepsilon$

QED

思考： 看似 $③$ 条件比 $④$ 条件弱很多，它只取了一个分划，但通过证明得知，它们其实是等价的。这说明仅仅利用 $③$ 中的一个分划，是可以确定 $④$ 中的 $\delta$ 条件的，并且将 $④$ 中的分划 $\pi$ 都很好的限制在了 $③$ 这一个分划当中。

Lebesgue 外侧度

定义开方体： $\displaystyle Q=\prod_{i=1}^n(a_i, b_i)$，“体积”：$\displaystyle V(Q)=\prod\limits_{i=1}^n(b_i-a_i)$

定义8 （Lebesgue 外侧度）

设 $A\subset \mathbb{R}^n$，记

$$m^*(A) = \inf\left\{\sum_{j\in J} V(Q_j): J\text{为可数集}, Q_j\text{为开方体}, A\subset\bigcup_{j\in J} Q_j\right\}$$

称为 $A$ 的 $n$ 维 $Lebesgue$ 外侧度。（就是用很多的集合将 $A$ 包住，取它们中“体积”最小的）

定义9 （Lebesgue 零测集）

如果 $A\subset\mathbb{R}^n, m^*(A)=0$，则称 $A$ 为 $Lebesgue$ 零测集。

性质

1. $m^*(\varnothing) = 0, 0\leqslant m^*(A)\leqslant +\infty$

2. 若 $A, A_k\subset \mathbb{R}^n$，$A\subset\bigcup\limits_{k=1}^\infty A_k$，则 $m^*(A)\leqslant \sum\limits_km^*(A_k)$

3. 若 $A\subset B\subset \mathbb{R}^n$，则 $m^*(A)\leqslant m^*(B)$

4. 若 $A_k\subset\mathbb{R}^n$，则 $m^*(\bigcup\limits_{k=1}^\infty A_k)\leqslant \sum\limits_{k=1}^\infty m^*(A_k)$

5. 设 $A\subset \mathbb{R}^n, r > 0$ 记 $A+b:=\{x+b:x\in A\}$，则 $m^*(A+b)=m^*(A)$

6. 设 $A\subset \mathbb{R}^n, r>0$ 记 $rA:=\{rx:x\in A\}$，则 $m^*(rA)=r^nm^*(A)$

7. 若 $Q\subset \mathbb{R}^n$ 为开方体，则 $m^*(Q) = V(Q) = m^*(\overline{Q})$

几个例题

例1：$m^*(\{a\}) = 0$。

例2：$m^*(\{a_1,a_2,\ldots\})\leqslant \sum\limits_i m^*(\{a_i\}) = 0$。（这里可以有无限个 $a_i$ 只要是可数个即可）

命题10 （低维函数在高维中的图像测度为0）

设 $K\subset \mathbb{R}^{n-1}$ 为紧集，$f\in C(K)$（$C(K)$：在 $K$ 上连续的函数集合），
记 $F=\text{graph } f=\{(x, f(x)):x\in K\}$，则 $m^*(F) = 0$。

思路：由于 $K$ 是紧集并且 $f$ 在 $K$ 上连续，则 $f$ 在 $K$ 上一致连续。
则有 $|x_1-x_2|\leqslant \delta$，$|f(x_1)-f(x_2)|\leqslant \varepsilon$，做 $K$ 上的分划 $\pi$，保证 $\forall q\in\pi$，有 $\text{diam }q\leqslant \delta$，则 $w_q\leqslant \varepsilon$，令 $f(q)\subset I_q$，这样就可以用 $K\times I_q$ 将 $F$ 覆盖，由于 $m^*(I_q)\leqslant \varepsilon$，则 $m^*(F)$ 也可以被 $\varepsilon$ 限制了。

推论：$Q\subset \mathbb{R}^n$ 是一个闭方体，则 $m^*(\partial Q) = 0$。

定理11 （间断点构成 Lebesgue 零测集 $\iff$ Riemann 可积）

设 $Q\subset \mathbb{R}^n$ 为闭方体，$f:Q\rightarrow \mathbb{R}$ 有界，记 $D(f) = \{x\in Q:f\text{在} x \text{处不连续}\}$，则 $f\ Riemann$ 可积 $\iff$ $m^*(D(f)) = 0$。

证明方法和一维的推导方法类似。

推论：若 $f\in C(Q)$ 则 $f\ Riemann$ 可积。