设 π ( a ∣ s ; θ ) \pi(a|s;\theta) π ( a ∣ s ; θ ) θ \theta θ V π ( S ) V_\pi(S) V π ( S )
max θ E S [ V π ( S ) ] = : J ( θ ) \max_\theta\mathbb{E}_S[V_{\pi}(S)] =: J(\theta)
θ max E S [ V π ( S ) ] = : J ( θ )
由带基线的策略梯度定理 可知:
∂ J ( θ ) ∂ θ = E S [ E A ∼ π ( ⋅ ∣ S ; θ ) [ ( Q π ( S , A ) ) − V π ( S ) ∇ θ ln π ( A ∣ S ; θ ) ] ] \frac{\partial J(\theta)}{\partial \theta} =
\mathbb{E}_S[\mathbb{E}_{A\sim\pi(\cdot|S;\theta)}[(Q_{\pi}(S,A)) - V_{\pi}(S)\nabla_{\theta}\ln\pi(A|S;\theta)]]
∂ θ ∂ J ( θ ) = E S [ E A ∼ π ( ⋅ ∣ S ; θ ) [ ( Q π ( S , A ) ) − V π ( S ) ∇ θ ln π ( A ∣ S ; θ ) ] ]
设 v ( s ; w ) v(s;w) v ( s ; w ) π ( a ∣ s ; θ ) \pi(a|s;\theta) π ( a ∣ s ; θ ) w w w ( s , a , r , s ′ ) (s,a,r,s') ( s , a , r , s ′ ) Q π ( s , a ) Q_\pi(s,a) Q π ( s , a )
Q π ( s , a ) ≈ r + γ ⋅ v ( s ′ ; w ) Q_\pi(s,a)\approx r + \gamma\cdot v(s';w)
Q π ( s , a ) ≈ r + γ ⋅ v ( s ′ ; w )
则近似策略梯度可以表示为:
J ( θ ) ∂ θ ≈ ( r + γ ⋅ v ( s ′ ; w ) − v ( s ; w ) ) ∇ θ ln π ( a ∣ s ; θ ) \frac{J(\theta)}{\partial\theta} \approx (r+\gamma\cdot v(s';w) - v(s;w))\nabla_\theta\ln\pi(a|s;\theta)
∂ θ J ( θ ) ≈ ( r + γ ⋅ v ( s ′ ; w ) − v ( s ; w ) ) ∇ θ ln π ( a ∣ s ; θ )
对于由策略 π ( a ∣ s ; θ ) \pi(a|s;\theta) π ( a ∣ s ; θ ) ( s , a , r , s ′ ) (s,a,r,s') ( s , a , r , s ′ )
TD target : y ^ = r + γ ⋅ v ( s ′ ; w ) \hat{y} = r + \gamma\cdot v(s';w) y ^ = r + γ ⋅ v ( s ′ ; w )
Loss: L ( w ) = 1 2 ∣ ∣ v ( s ; w ) − y ^ ∣ ∣ 2 2 = 1 2 ∣ ∣ δ ∣ ∣ 2 2 \mathcal{L}(w) = \frac{1}{2}||v(s;w)-\hat{y}||_2^2 = \frac{1}{2}||\delta||_2^2 L ( w ) = 2 1 ∣ ∣ v ( s ; w ) − y ^ ∣ ∣ 2 2 = 2 1 ∣ ∣ δ ∣ ∣ 2 2 δ = v ( s ; w ) − y ^ \delta = v(s;w) - \hat{y} δ = v ( s ; w ) − y ^ TD error
Approximate gradient: g = ( y ^ − v ( s ; w ) ) ∇ θ ln π ( a ∣ s ; θ ) = − δ ⋅ ∇ θ ln π ( a ∣ s ; θ ) g = (\hat{y}-v(s;w))\nabla_\theta\ln\pi(a|s;\theta) = -\delta\cdot\nabla_\theta\ln\pi(a|s;\theta) g = ( y ^ − v ( s ; w ) ) ∇ θ ln π ( a ∣ s ; θ ) = − δ ⋅ ∇ θ ln π ( a ∣ s ; θ )
Update value network: w ← w − α ∂ L ( w ) ∂ w = w − α δ ⋅ ∇ w v ( s ; w ) w\gets w - \alpha \frac{\partial\mathcal{L}(w)}{\partial w} = w - \alpha\delta\cdot \nabla_wv(s;w) w ← w − α ∂ w ∂ L ( w ) = w − α δ ⋅ ∇ w v ( s ; w )
Updata policy network: θ ← θ + β g = θ − β δ ⋅ ∇ θ ln π ( a ∣ s ; θ ) \theta\gets\theta + \beta g = \theta - \beta\delta\cdot \nabla_{\theta}\ln\pi(a|s;\theta) θ ← θ + β g = θ − β δ ⋅ ∇ θ ln π ( a ∣ s ; θ )
在KataRL 中用JAX实现了A2C算法,核心代码a2c_jax.py ,超参数文件 ,不同环境下与其他模型的比较 。
可以看出A2C的效果较差且慢,但是其实现较为简单,以后可以进一步用GAE对其进行优化(类似PPO算法)。测试代码:
python katarl/run/a2c/a2c.py --train --wandb-track
python katarl/run/a2c/a2c.py --train --wandb-track --env-name Acrobot-v1Cartpole environment information - Gymnasium
Agent
model struct:
Input(4)-Dense(32)-Dense(32)-Output (We call it origin one)
Input(4)-Dense(128)-Dense(64)-Dense(16)-Output (We call it deeper one)
model optimizer & learning rate (After multi test, get the best args, maybe~)
Adam: α = 1 0 − 3 , β = 1 0 − 5 \alpha=10^{-3}, \beta=10^{-5} α = 1 0 − 3 , β = 1 0 − 5
SGD: α = 5 × 1 0 − 4 , β = 1 0 − 4 \alpha=5\times 10^{-4}, \beta = 10^{-4} α = 5 × 1 0 − 4 , β = 1 0 − 4
Environment
positive reward r p o s = 1 r_{pos} = 1 r p o s = 1
negative reward r n e g = − 10 r_{neg} = -10 r n e g = − 1 0 − 20 -20 − 2 0
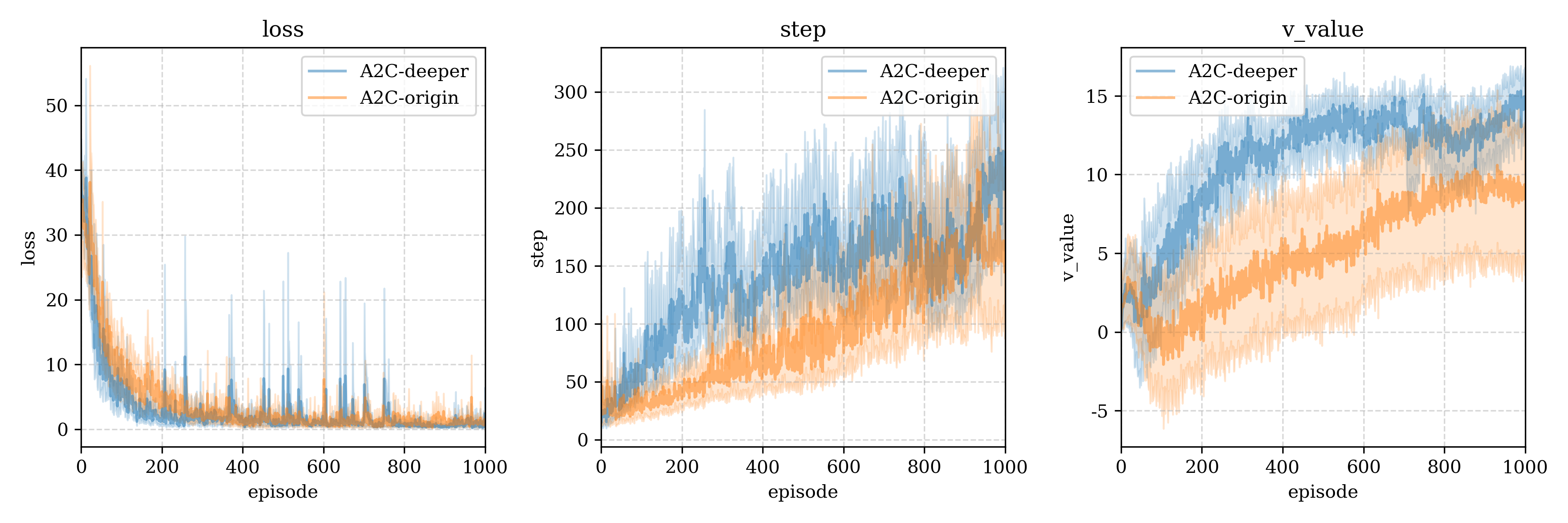
We try different model struct, origin and deeper model, after compare, we found the deeper is almost rolling the origin one.
我们尝试测试origin和deeper两种模型,更深的模型几乎完全碾压了浅的模型。
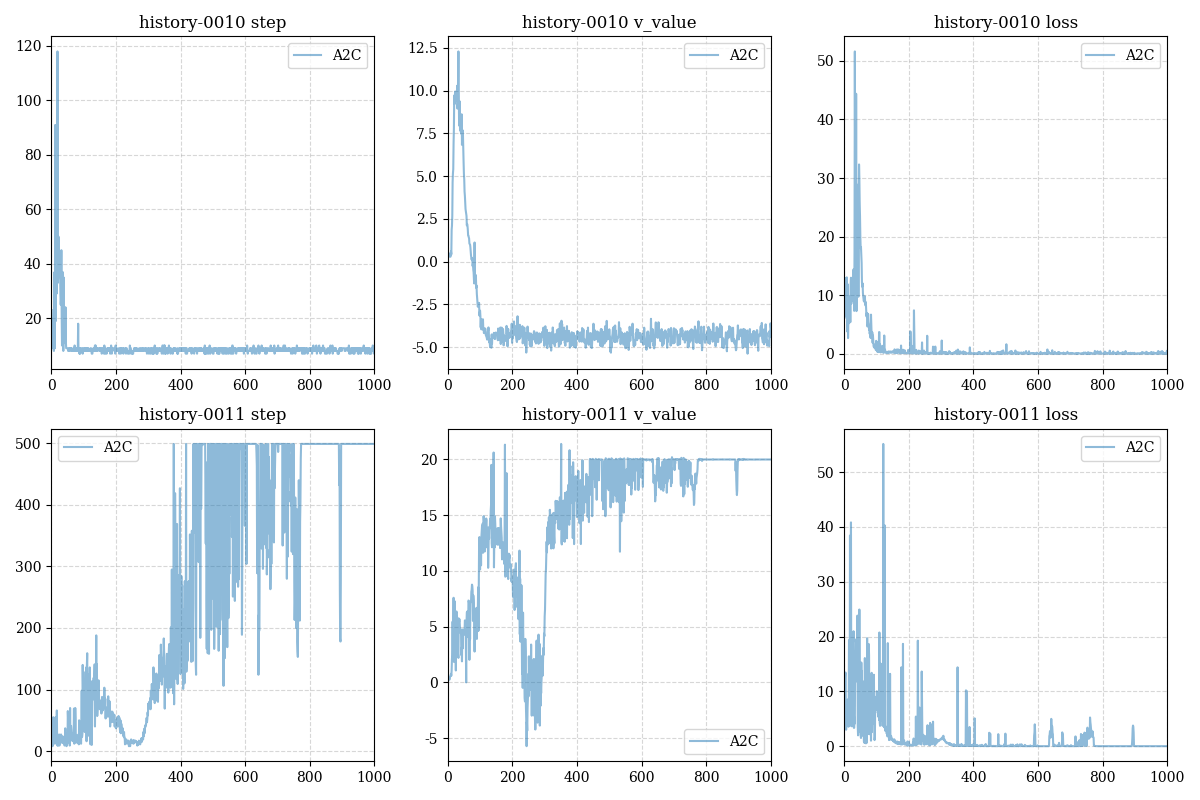
We also find the deeper model can avoid complete failure of the policy since random environment,this is the result of restarting the origin model twice: (one almost dead, and the other is powerful)
我们还发现更深的模型可以避免因环境随机性导致策略完全失效,以下是我们重启origin模型两侧得到的完全不同的两个结果(其中一个几乎无法走出10步,而另一个几乎获得了最优策略)
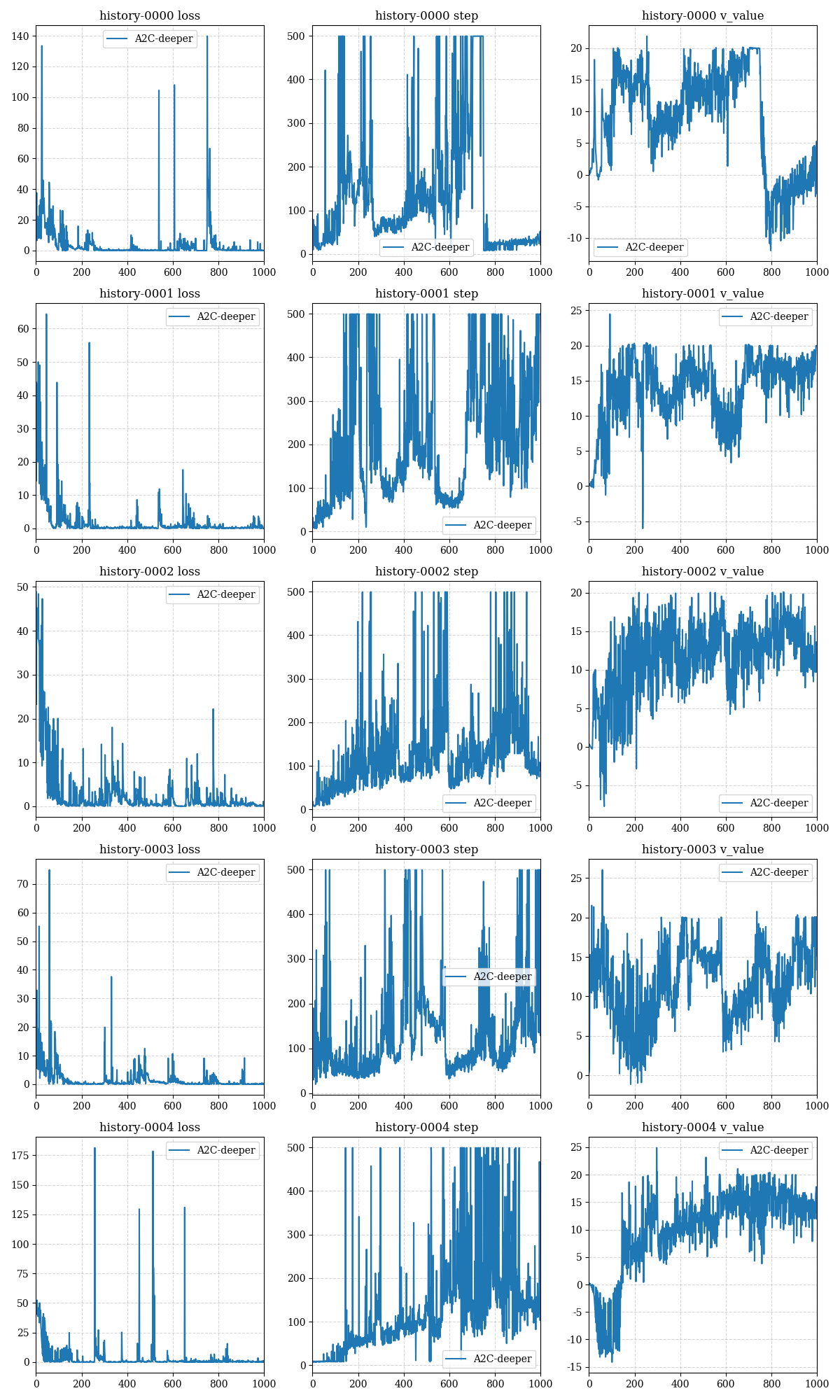
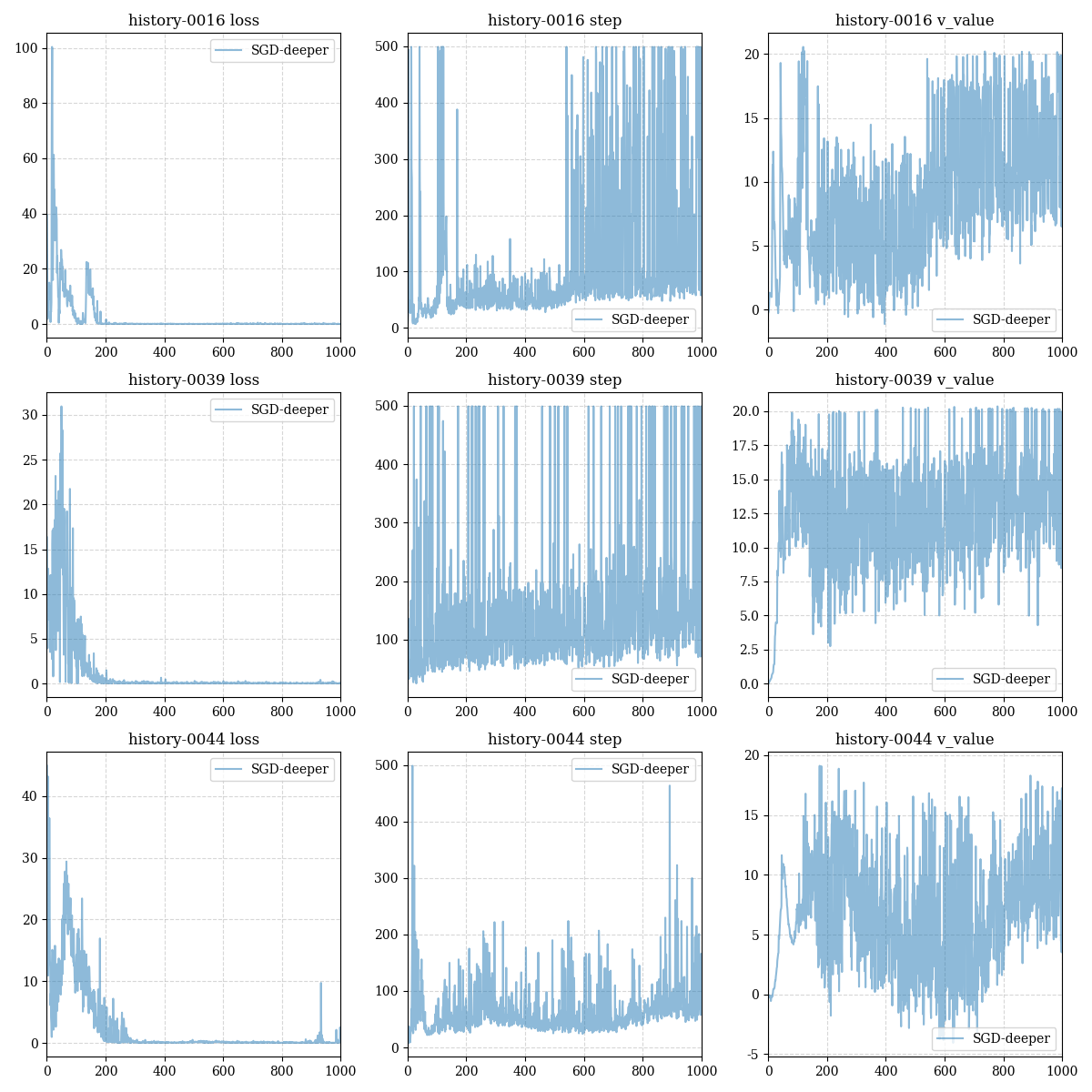
The training results of 5 restarts of the deeper model are given below:
以下给出了5次重启deeper model的训练结果:
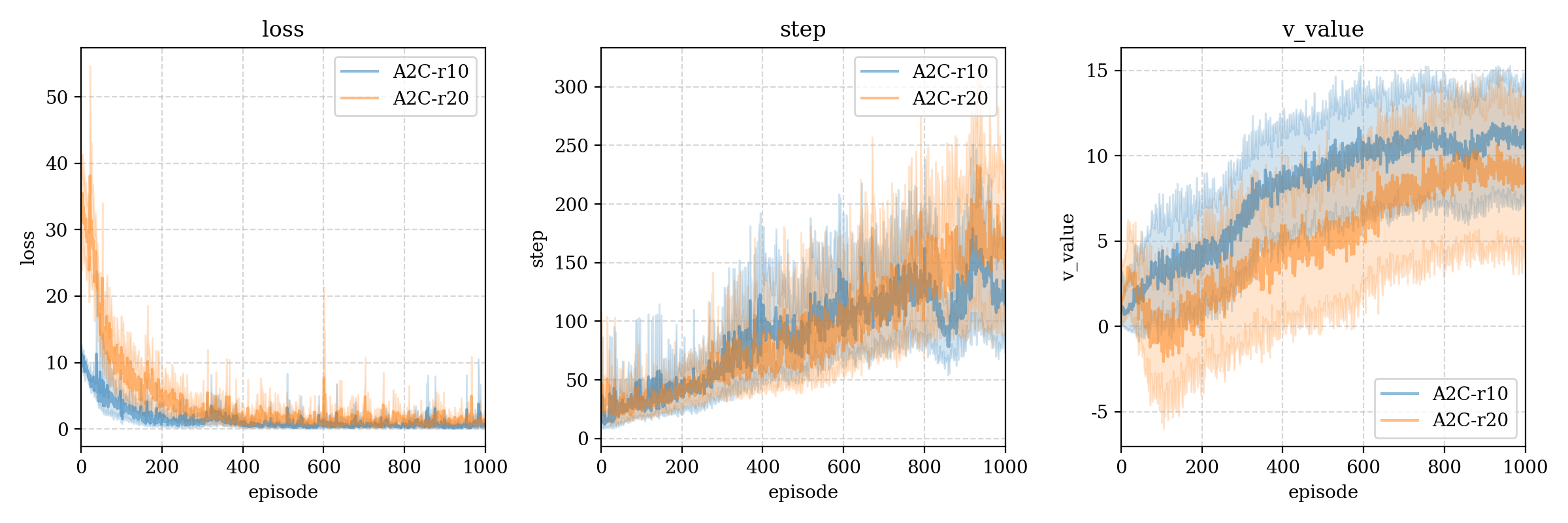
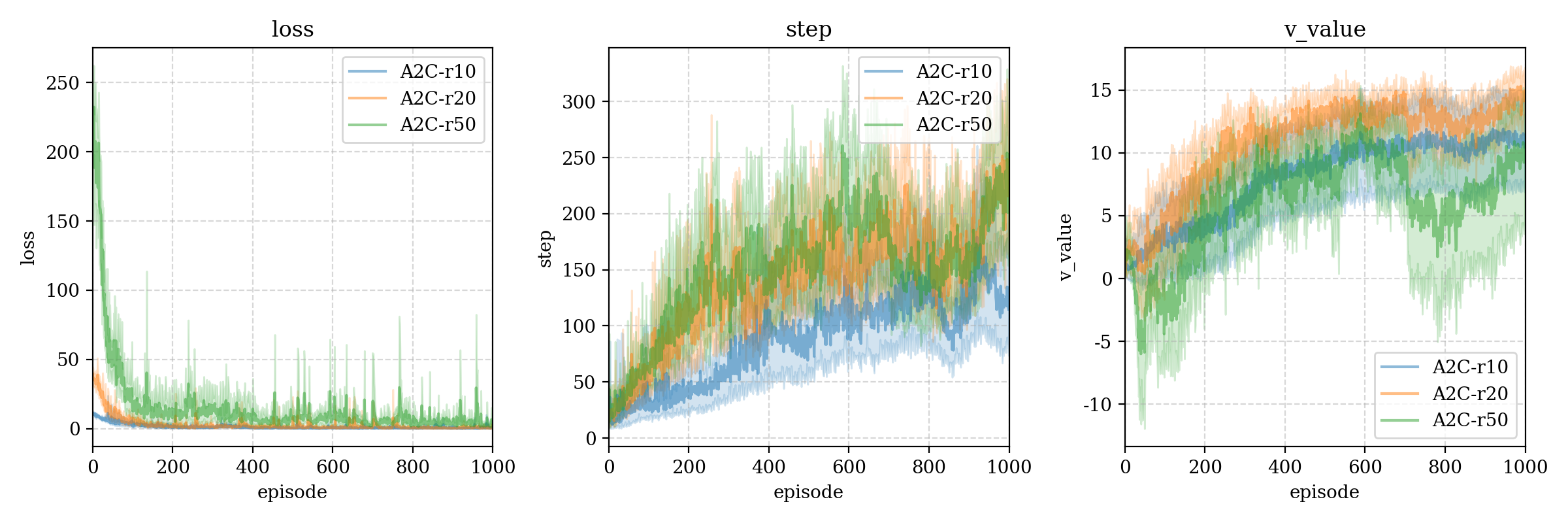
我们又尝试了两种不同的失败损失,如果平衡木在没有达到最长步数(500)时失去平衡,那么最后一个动作就会获得 − 10 -10 − 1 0 − 20 -20 − 2 0 r10 和 r20,根据比对,我们发现更大的失败损失确实能提高达到更高step的可能(可能因为这样critic能给出更准确的判断?因为如果记失败损失是 r n e g r_{neg} r n e g γ = 0.95 \gamma=0.95 γ = 0 . 9 5
1 + γ + ⋯ γ n − 1 − r n e g ⋅ γ n = 0 ⇒ n = log 0.95 1 1 + r n e g / 20 1+\gamma+\cdots\gamma^{n-1}-r_{neg}\cdot \gamma^{n} = 0\Rightarrow n = \log_{0.95}\frac{1}{1+r_{neg}/20}
1 + γ + ⋯ γ n − 1 − r n e g ⋅ γ n = 0 ⇒ n = log 0 . 9 5 1 + r n e g / 2 0 1
带入 r n e g = 10 , 20 r_{neg}=10,20 r n e g = 1 0 , 2 0 n ≈ 8 , 13 n\approx 8, 13 n ≈ 8 , 1 3 r n e g r_{neg} r n e g
在critic评估正确的情况下,critic可以在actor最终失败前 n n n
在critic评估错误的情况下,在失败前的相同步数时,更大的 r n e g r_{neg} r n e g
r r e g r_{reg} r r e g n n n r n e g r_{neg} r n e g l o g log l o g deeper模型下不同的失败损失大小:
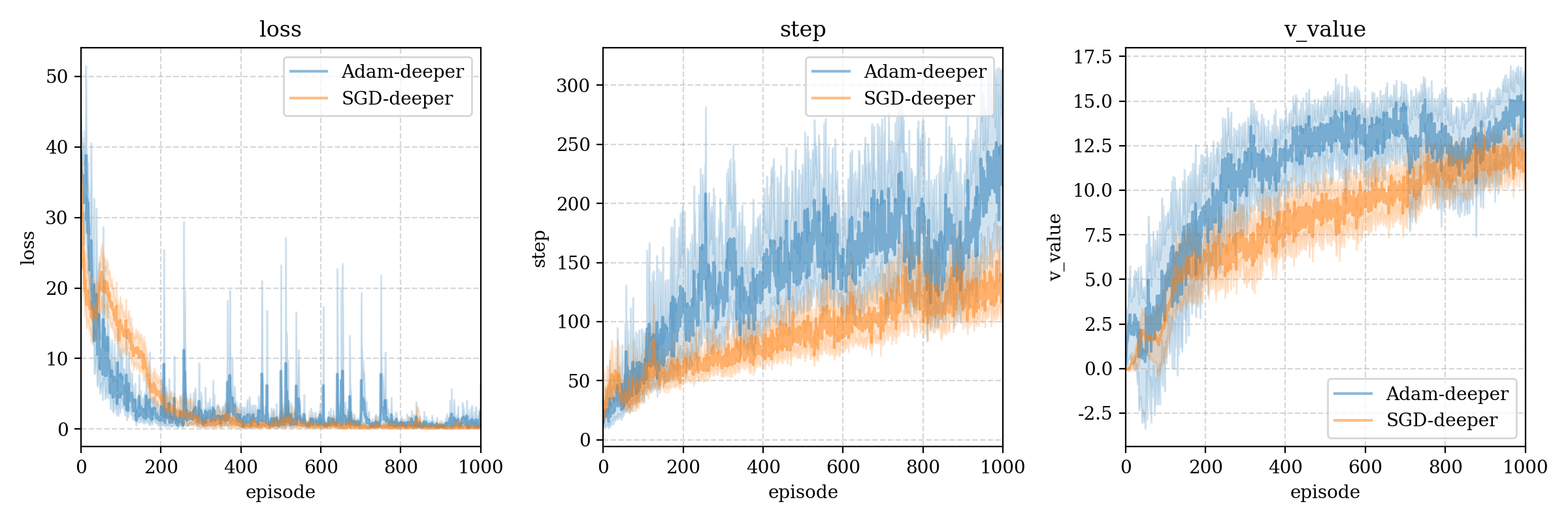
我们尝试两种优化器 Adam 和 SGD(学习率上文已经给出),在deeper网络结构下的比较:
可以看出基本上Adam碾压了SGD,但是SGD优化器竟有时可以在第一个step中达到最优,虽然支撑不了几步: