使用tinyrenderer入门OpenGL
我的github项目链接, 包含全部完整代码和三维图像数据.
介绍
我们使用的是来自 tinyrenderer 的github项目: 使用C++从零开始建立一个光栅化渲染器, 能够帮助我们入门OpenGL并理解其原理. 它所依赖库非常少, 包含他写的两个库文件, tgaimage.cpp, tgaimage.h 和 .obj 3D模型文件读取库 model.cpp, model.h 和 几何类型库 geometry.h.
它可以将当前视角的图像输出为 .tga 格式的文件, 可以使用 PhotoShop 进行预览和修改, 我们使用的是 PhotoShop CS6 版本, g++ 编译器版本为 8.1.0.
中文教程参考: KrisYu 的github项目和 知乎 - 从零构建光栅器,tinyrenderer笔记 对应的github项目 MrZz233/tinyrenderer_notes
由于该简单渲染器并不支持鼠键交互功能, 所以我们打算使用该项目完成作业前两个部分, 即
- 网络顶点和边的非消隐外观显示;
- 网络顶点、边和多边形的动态隐藏元素去除;
其中第二部分我们打算使用Z-buffer算法完成.
后三个部分
- 鼠标, 键盘交互实现模型旋转, 视野放大等;
- 选择显示环境光, 漫反射(Lambert模型), 镜面反射(Phong模型)光照效应的面绘制效果;
- 选择显示Gouraud明暗处理和Phong明暗处理的面绘制效果.
*. 选择独特的网络模型进行可视化.
我们打算使用Unity3D完成.
基础命令
编译方法
假设我们写的程序为main.cpp, 并且和文件tgaimage.cpp, tgaimage.h, model.cpp, model.h, geometry.h, 放在了同一个文件夹下.
编译命令(使用g++的链接编译)
g++ main.cpp tgaimage.cpp model.cpp -o main编译并运行
g++ main.cpp tgaimage.cpp model.cpp -o main && main.exe && output.tga源代码理解
由于我们是第一次接触OpenGL所以对其命令没有任何了解, 只能自己摸索查阅资料, 每部分我会根据结合源代码和别人所写的代码, 给出对命令的解释, 可能并不准确.
绘制点与线
基础命令
根据 tgaimage.h 查看源码, 发现它主要由两部分组成, 分别为 颜色设置(TGAColor) 和 画布设置(TGAImage).
// 颜色设置
TGAColor red = TGAColor(255, 0, 0, 255); // 颜色数据类型, 由RGBA色彩空间确定, 其中RGB是我们熟知的三原色, A为透明度.
//画布设置
TGAImage image(w, h, bpp); // w: width, 长; h: height, 宽; bpp: 使用的颜色参数, 这里有三个配置选项, TGAImage::RGRAYSCALE, TGAImage::RGB, TGAImage::RGBA, 如果没有理解错应该分别是: 灰度, RGB三原色, RGBA色彩空间, 它们的参数值分别为1, 3, 4, 根据这个参数, 可以确定画布的色域.
image.set(x, y, red); // 设置(x, y)坐标处的像素颜色为red
image.flip_vertically(); // 将画布竖向旋转
image.flip_horizontally(); // 将画布横向旋转
image.write_tga_file("output.tga"); // 将画布信息以tga文件格式输出出来点的绘制
绘制四个不同颜色的点
#include <bits/stdc++.h>
#include "tgaimage.h"
const TGAColor white(255, 255, 255);
const TGAColor red(255, 0, 0);
const TGAColor green(0, 255, 0);
const TGAColor blue(0, 0, 255);
int main() {
TGAImage image(6, 6, TGAImage::RGB);
image.set(0, 0, red);
image.set(5, 5, blue);
image.set(0, 5, green);
image.set(5, 0, white);
image.write_tga_file("output.tga");
return 0;
}
绘制交错的点
#include <bits/stdc++.h>
#include "tgaimage.h"
const TGAColor white(255, 255, 255);
const TGAColor red(255, 0, 0);
const TGAColor green(0, 255, 0);
const TGAColor blue(0, 0, 255);
int main() {
TGAImage image(6, 6, TGAImage::RGB);
for (int i = 0; i < 6; i++) {
for (int j = 0; j < 6; j++) {
if ((i + j) & 1) {
image.set(i, j, red);
} else {
image.set(i, j, white);
}
}
}
// image.flip_vertically();
image.write_tga_file("output.tga");
return 0;
} 水平旋转后
水平旋转后

线的绘制
根据两点 和 , 绘制出两点间的线段, 由插值多项式可知, 两点间直线可以表示为
设 , 于是 , 由于像素点都是离散的, 我们考虑递增 坐标, 计算每一个对应的, 再绘制出来.
但是这样有一个问题, 如果两点间的斜率 , 由于 是离散递增的, 即变化量为 , 所以 的变化可能是阶跃的, 这样就导致线是间断的了(见下左图), 所以这种情况下, 我们需要对 坐标进行递增绘图, 为简化代码, 考虑直接交换 坐标即可.
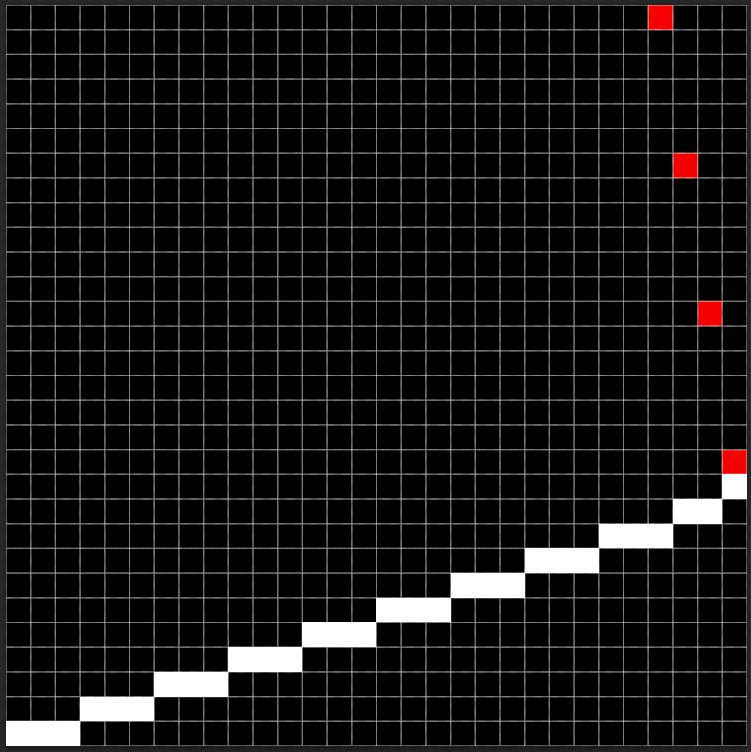 对进行递增后
对进行递增后
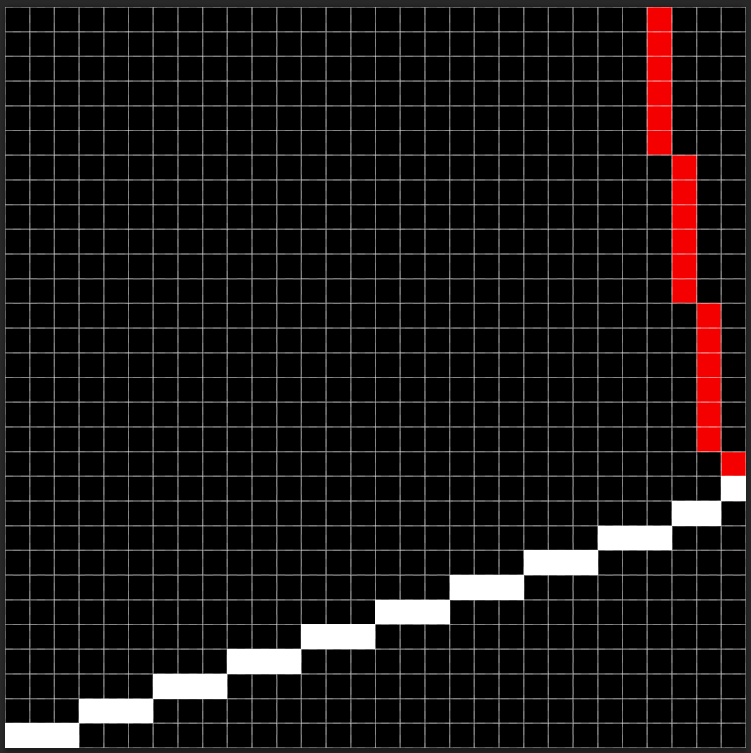
#include <bits/stdc++.h>
#include "tgaimage.h"
const double eps = 1e-5;
const TGAColor white(255, 255, 255);
const TGAColor red(255, 0, 0);
const TGAColor green(0, 255, 0);
const TGAColor blue(0, 0, 255);
void line(int x0, int y0, int x1, int y1, TGAColor color, TGAImage &image) {
bool fg = false;
if (1.0 * std::abs(y1-y0) / std::abs(x1-x0) > 1) { // 如果斜率>1, 则根据y轴递增绘制线段, 否则线段不连续, 直接交换x,y轴, 并用fg记录下来
std::swap(x0, y0);
std::swap(x1, y1);
fg = true;
}
if (x0 > x1) { // 保证(x0, y0)在(x1, y1)的左侧
std::swap(x0, x1);
std::swap(y0, y1);
}
for (int x = x0; x <= x1; x++) {
double t = 1.0 * (x - x0) / (x1 - x0);
int y = t * y1 + (1-t) * y0;
if (!fg) image.set(x, y, color);
else image.set(y, x, color); // 反转了x,y轴
}
}
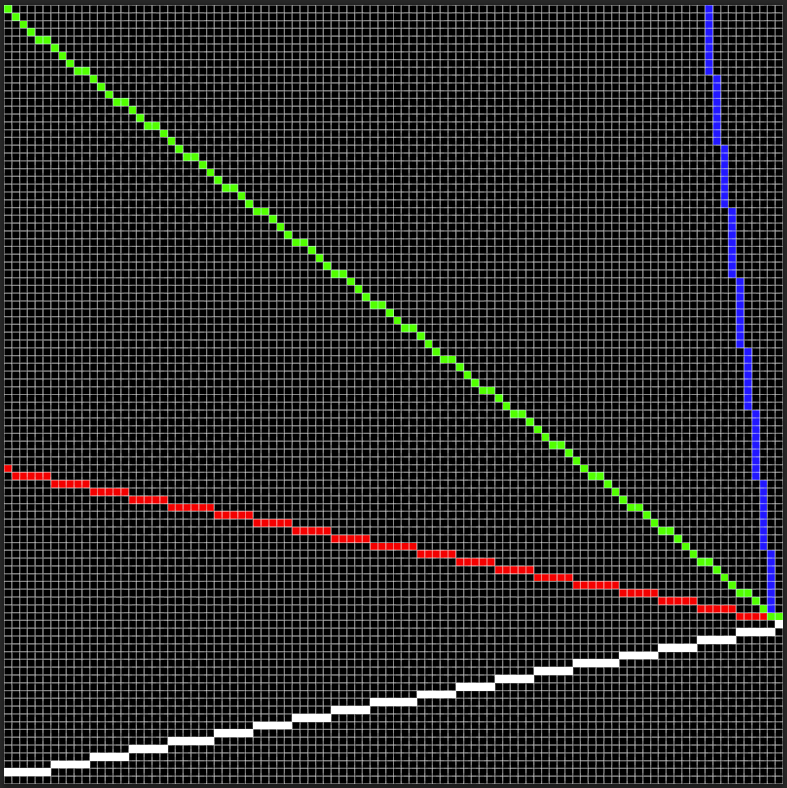
int main() {
TGAImage image(100, 100, TGAImage::RGB);
line(0, 1, 99, 20, white, image);
line(99, 21, 0, 40, red, image);
line(99, 21, 90, 99, blue, image);
line(99, 21, 0, 99, green, image);
image.write_tga_file("output.tga");
return 0;
}
绘制线框模型
我们使用了github - tinyrenderer
项目中所提供的免费模型.
我们知道 .obj 文件一种3D模型文件格式, 这里我们先将其打开, 并绘制出线框模型.
obj文件格式
这里打开第一个非洲人脸模型的数据(省略号省略过多的类似信息)
v -0.000581696 -0.734665 -0.623267
v 0.000283538 -1 0.286843
v -0.117277 -0.973564 0.306907
...
# 1258 vertices
vt 0.532 0.923 0.000
vt 0.535 0.917 0.000
vt 0.542 0.923 0.000
...
# 1339 texture vertices
vn 0.001 0.482 -0.876
vn -0.001 0.661 0.751
vn 0.136 0.595 0.792
...
# 1258 vertex normals
g head
s 1
f 24/1/24 25/2/25 26/3/26
f 24/1/24 26/3/26 23/4/23
f 28/5/28 29/6/29 30/7/30
...
# 2492 faces我们先研究 v 和 f 开头的信息.
-
v后面的三个坐标分别为该顶点的x,y,z坐标, 其中 , 每一行就代表一个顶点的全部信息. -
f 24/1/24 25/2/25 26/3/26表示一个模型的三角面, 一个三角面由三个顶点构成. 一个面由三组信息构成, 每组信息的一个数据表示顶点的序号, 这个例子表示: 该面由序号 三个顶点组成这里的顶点顺序由v的读入顺序确定.
obj文件读取方式
我们在和主函数相同的目录创建名为 obj 的文件夹用于存放 .obj 文件, 并在和主函数相同的目录中新加入三个头文件 geometry.h, model.h, model.cpp, 第一个用于存储几何数据, 如三维和二维中一个点的相关数据, 类名称分别为 Vec3 和 Vec2, 其源代码如下, 我们加入了对其的解释
template <class t> struct Vec3 {
union {
struct {t x, y, z;}; // 顶点的三维坐标
struct { t ivert, iuv, inorm; };
t raw[3];
};
Vec3() : x(0), y(0), z(0) {} // 默认初始化为原点
Vec3(t _x, t _y, t _z) : x(_x),y(_y),z(_z) {}
inline Vec3<t> operator ^(const Vec3<t> &v) const { return Vec3<t>(y*v.z-z*v.y, z*v.x-x*v.z, x*v.y-y*v.x); } // 向量外积
inline Vec3<t> operator +(const Vec3<t> &v) const { return Vec3<t>(x+v.x, y+v.y, z+v.z); } // 向量相加
inline Vec3<t> operator -(const Vec3<t> &v) const { return Vec3<t>(x-v.x, y-v.y, z-v.z); } // 向量相减
inline Vec3<t> operator *(float f) const { return Vec3<t>(x*f, y*f, z*f); } // 向量伸缩f倍
inline t operator *(const Vec3<t> &v) const { return x*v.x + y*v.y + z*v.z; } // 向量内积
float norm () const { return std::sqrt(x*x+y*y+z*z); } // 模长
Vec3<t> & normalize(t l=1) { *this = (*this)*(l/norm()); return *this; } // 单位方向
template <class > friend std::ostream& operator<<(std::ostream& s, Vec3<t>& v); // 重载输出格式
};
typedef Vec3<float> Vec3f; // 浮点形式的坐标
typedef Vec3<int> Vec3i; // 整点形式的坐标第二个和第三个用于读取文件, 我们从 Model 类来看
class Model {
private:
std::vector<Vec3f> verts_; // 顶点数组
std::vector<std::vector<int> > faces_; // 面数组
public:
Model(const char *filename); // 构造函数(文件位置)
~Model(); // 析构函数
int nverts(); // 返回顶点个数
int nfaces(); // 返回面的个数
Vec3f vert(int i); // 返回verts_[i]
std::vector<int> face(int idx); // 返回faces_[idx]
};Model 类给出了一个模型所有的数据, vert是vertex的缩写, 即顶点; face是三角面.
-
私有变量的动态数组
verts_, faces_分别存储该模型的顶点和面的数据, 其中verts_是一维动态数组, 而faces_是二维动态数组(因为其中要存储三个顶点的数据). -
函数
nverts(), nfaces()能够返回当前模型所拥有的的顶点数和面数, 对应于私有变量动态数组verts_, faces_的大小, 即返回verts_.size(), faces_.size(). -
函数
vert(int i), face(int idx)分别用于访问私有数组verts_, faces_中的元素, 即返回verts_[i], faces_[idx].
下面代码给出了如何使用 Model.h 来读取文件和显示线框图.
#include <bits/stdc++.h>
#include "tgaimage.h" // tga画图库
#include "model.h" // 模型库, 实现模型读取
#include "geometry.h" // 几何库, 定义顶点数据Vec2和Vec3
const TGAColor white(255, 255, 255);
const int width = 800;
const int height = 800;
int main() {
Model *model = new Model("obj/african_head.obj"); // 读取模型
// Model *model = new Model("obj/monster.obj");
// Model *model = new Model("obj/.obj");
TGAImage image(width, width, TGAImage::RGB); // 创建画布
for (int i = 0; i < model->nfaces(); i++) {
std::vector<int> face = model->face(i);
for (int j = 0; j < 3; j++) {
// 取出三角面中相邻的两个顶点
Vec3f v0 = model->vert(face[j]);
Vec3f v1 = model->vert(face[(j+1)%3]);
// 做拉伸变换从 (-1, -1)->(0, 0), (1, 1)->(width, height)
int x0 = (v0.x+1) * width / 2;
int x1 = (v1.x+1) * width / 2;
int y0 = (v0.y+1) * height / 2;
int y1 = (v1.y+1) * height / 2;
line(x0, y0, x1, y1, white, image);
}
}
image.write_tga_file("output.tga"); // line函数和上文相同
delete model;
return 0;
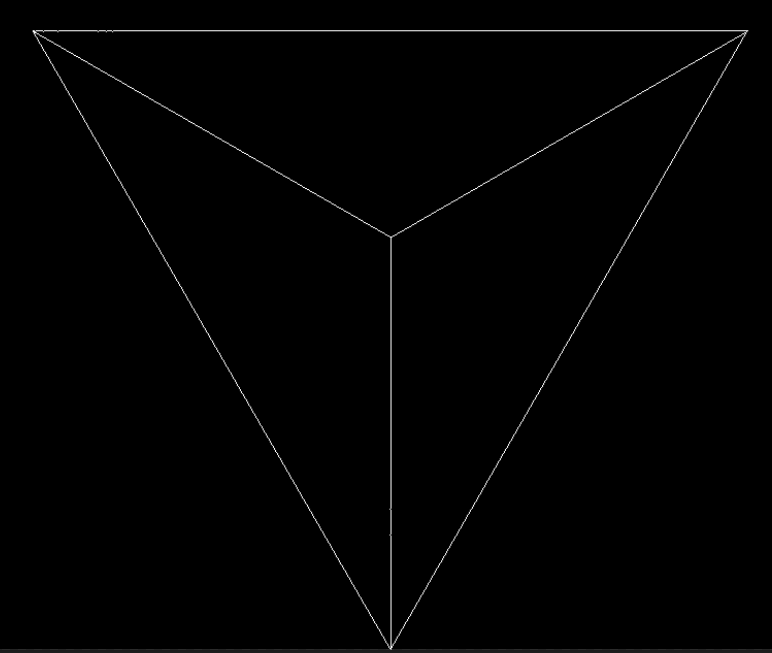
}该视角为沿z正轴方向投影图.


平面着色
我们已经会绘三角形面了, 接下来研究如何对三角形进行染色, 使我们的图片更加好看, 有立体感.
不难想到, 填充三角形内部可以绘制一条条横线段完成, 每一条横线左端点为三角形的左边的边界, 右端点为右边的边界, 我们先对y轴坐标排序, 然后对每个x计算左端点和右端点坐标即可.
假设三角形三个坐标为 且 . 我们可以把当前扫到的 轴坐标视为一条扫描线, 从下至上扫过去, 每次对扫描线上三角形内部点进行填充.
-
扫描线的左端点计算比较容易, 根据 即可得出.
-
右端点需要确定当前的扫描线有没有经过中间的顶点, 假设当前右端点在线段 上, 则 , 初始时 , 当扫描线 时, .
#include <bits/stdc++.h>
#include "tgaimage.h" // tga画图库
#include "model.h" // 模型库, 实现模型读取
#include "geometry.h" // 几何库, 定义顶点数据Vec2和Vec3
const double eps = 1e-5;
const TGAColor white(255, 255, 255);
const TGAColor red(255, 0, 0);
const TGAColor green(0, 255, 0);
const TGAColor blue(0, 0, 255);
void line(Vec2i v0, Vec2i v1, TGAColor color, TGAImage &image) {
bool fg = false;
if (1.0 * std::abs(v1.y-v0.y) / std::abs(v1.x-v0.x) > 1) { // 如果斜率>1, 则根据y轴递增绘制线段, 否则线段不连续, 直接交换x,y轴, 并用fg记录下来
std::swap(v0.x, v0.y);
std::swap(v1.x, v1.y);
fg = true;
}
if (v0.x > v1.x) { // 保证(x0, y0)在(x1, y1)的左侧
std::swap(v0, v1);
}
for (int x = v0.x; x <= v1.x; x++) {
double t = 1.0 * (x - v0.x) / (v1.x - v0.x);
int y = t * v1.y + (1-t) * v0.y;
if (!fg) image.set(x, y, color);
else image.set(y, x, color); // 反转了x,y轴
}
}
void fill(Vec2i v0, Vec2i v1, Vec2i v2, TGAColor color, TGAImage &image, bool outline=false) {
if (v0.y == v1.y && v0.y == v2.y) return; // 如果y轴相等则无法填充颜色
// 简单冒泡排序, 使得 v0.y < v1.y < v2.y
if (v0.y > v1.y) std::swap(v0, v1);
if (v0.y > v2.y) std::swap(v0, v2);
if (v1.y > v2.y) std::swap(v1, v2);
Vec2i vt = v0; // 存储当前(x1,y1)连接的顶点
for (int y = v0.y; y <= v2.y; y++) {
int l = v0.x + 1.0 * (y - v0.y) / (v2.y - v0.y) * (v2.x - v0.x);
if (y > v1.y || v0.y == v1.y) vt = v2; // 扫过中间点时或v0和v1的y坐标相同时, 交换(x1,y1)连接的顶点, 避免除以0导致程序错误
int r = v1.x + 1.0 * (y - v1.y) / (vt.y - v1.y) * (vt.x - v1.x);
if (l > r) std::swap(l, r);
for (int x = l; x <= r; x++) image.set(x, y, color);
}
if (outline) { // 绘制轮廓线
line(v0, v1, red, image);
line(v0, v2, red, image);
line(v1, v2, red, image);
}
}
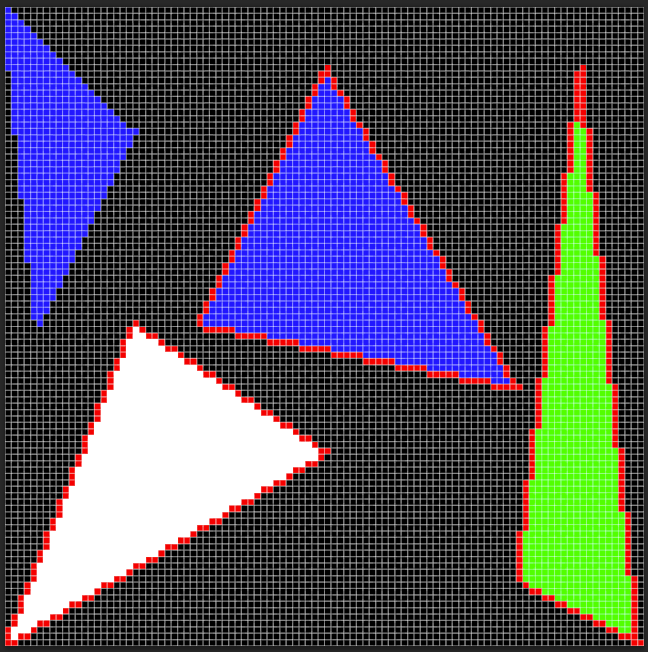
int main() {
TGAImage image(100, 100, TGAImage::RGB);
Vec2i v0 = Vec2i(0, 0), v1 = Vec2i(50, 30), v2 = Vec2i(20, 50);
fill(v0, v1, v2, white, image, true);
v0 = Vec2i(30, 50), v1 = Vec2i(80, 40), v2 = Vec2i(50, 90);
fill(v0, v1, v2, blue, image, true);
v0 = Vec2i(99, 0), v1 = Vec2i(80, 10), v2 = Vec2i(90, 90);
fill(v0, v1, v2, green, image, true);
v0 = Vec2i(0, 99), v1 = Vec2i(20, 80), v2 = Vec2i(5, 50);
fill(v0, v1, v2, blue, image, false);
image.write_tga_file("output.tga");
return 0;
}
我们接下来根据光照角度决定的光强, 对人脸绘制阴影, 以体现出其立体感, 这种方法称为Gouraud着色.
具体方法是, 先通过三角形的三个点, 计算出正面的法向量 , 给定光照的方向 , 利用内积即可计算出光照强度 .
// Gouraud着色
void draw(Vec3f light, Model *model, TGAImage &image, std::string filename) {
for (int i = 0; i < model->nfaces(); i++) {
std::vector<int> face = model->face(i);
std::vector<Vec2i> screen(3); // 存储图像坐标
std::vector<Vec3f> world(3); // 存储世界坐标
for (int j = 0; j < 3; j++) {
Vec3f tmp = model->vert(face[j]);
screen[j].x = (tmp.x + 1) * width / 2;
screen[j].y = (tmp.y + 1) * height / 2;
world[j] = tmp;
}
// 外积计算三角面的单位法向量
Vec3f n = ((world[2] - world[0]) ^ (world[1] - world[0])).normalize();
double intensity = n * light; // 内积计算光强
if (intensity > 0) { // 光强<0, 不进行绘制, 即背面裁剪
uint8_t c = 255 * intensity;
fill(screen[0], screen[1], screen[2], TGAColor(c, c, c), image);
}
}
image.write_tga_file(filename);
}
int main() {
Model *model = new Model("obj/african_head.obj");
// Model *model = new Model("obj/monster.obj");
TGAImage image(width, height, TGAImage::RGB);
draw(Vec3f(0, 0, -1), model, image, "output.tga");
delete model;
return 0;
}垂直光照

斜照射

其实该光照算法有明显的问题, 当法向量和入射光线夹角大于 时, 即外积为负数, 我们是不会进行绘制阴影的, 这就导致有很多暗色地方没有三角形面填充.
而且, 模型的嘴部由于有内腔的存在, 所以导致内部渲染将外部渲染覆盖掉了, 下面我们将用Z-buffer算法对其进行改进.
Z-buffer 算法
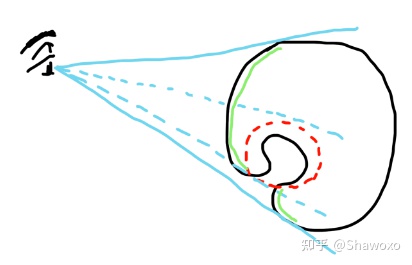
这张图很好的揭示了, 如何处理内腔, 当视线上有两个面同时存在时, 我们只需要将视线最前方的图像显示出来即可.
质心坐标
首先我们需要引入质心坐标这个概念, 对于一个 , 设点 为其内点
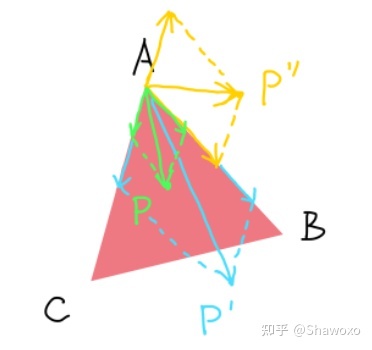
则向量 一定能表示为 的线性组合, 即
我们做一点变形可得
我们称 为点 对于 的质心坐标
于是可以得出以下结论:
点 在 的内部, 当且仅当, 对于 的质心坐标的每一维分量均大于 .
接下来考虑给出点 的坐标, 如何计算点 对于 的质心坐标. 由 式可知
最后一个等号原因: 通过 式可以看出 正是右边两个向量的外积方向上. 所以
且当 三点共线时 .
计算质心坐标的代码如下
//计算重心相对坐标, 返回(1-u-v, u, v)
Vec3f barycentric(Vec3f A, Vec3f B, Vec3f C, Vec3f P) {
Vec3f v[2];
v[0] = Vec3f(B.x - A.x, C.x - A.x, A.x - P.x);
v[1] = Vec3f(B.y - A.y, C.y - A.y, A.y - P.y);
Vec3f u = v[0] ^ v[1];
// 当ABC三点共线时, u.z=0, 无法绘制返回(-1,1,1)
if (std::abs(u.z) < eps) return Vec3f(-1, 1, 1);
return Vec3f(1-(u.x+u.y)/u.z, u.x/u.z, u.y/u.z);
}所以又有一种填充三角形的方法, 先将三角形用外接矩形框住, 然后枚举矩形中的每一个点, 如果该点在三角形内部则进行绘制, 否则不绘制.
Z-buffer算法
思路非常简单, 将每个像素到光源的最短距离计算出来, 然后对于同一个像素位置, 取最短距离的点进行绘制即可.
我们利用质心坐标可以很容易计算出每个像素的距离, 公式如下
我们先初始化一个和画布相同大小的数组 zbuffer, 用于储存当前每个像素点的到光源终点的最大距离(也就是更原理光源起点了), 初始值为最小值, 绘制的时候判断是否距离更大, 然后用较大值进行覆盖即可.
#include <bits/stdc++.h>
#include "tgaimage.h" // tga画图库
#include "model.h" // 模型库, 实现模型读取
#include "geometry.h" // 几何库, 定义顶点数据Vec2和Vec3
#define vd std::vector<double>
#define vdd std::vector<vd>
const double eps = 1e-5;
const TGAColor white(255, 255, 255);
const TGAColor red(255, 0, 0);
const TGAColor green(0, 255, 0);
const TGAColor blue(0, 0, 255);
const int width = 800;
const int height = 800;
Vec3f light; // 光源位置
//计算重心相对坐标, 返回(1-u-v, u, v)
Vec3f barycentric(Vec3f A, Vec3f B, Vec3f C, Vec3f P) {
Vec3f v[2];
v[0] = Vec3f(B.x - A.x, C.x - A.x, A.x - P.x);
v[1] = Vec3f(B.y - A.y, C.y - A.y, A.y - P.y);
Vec3f u = v[0] ^ v[1];
// 当ABC三点共线时, u.z=0, 无法绘制返回(-1,1,1)
if (std::abs(u.z) < eps) return Vec3f(-1, 1, 1);
return Vec3f(1-(u.x+u.y)/u.z, u.x/u.z, u.y/u.z);
}
// 将世界坐标转为图像坐标
Vec3f world2screen(Vec3f v) {
return Vec3f((int)((v.x + 1) * width / 2), (int)((v.y + 1) * height / 2), v.z);
}
void fill(std::vector<Vec3f> &pts, vdd &zbuffer, TGAColor color, TGAImage &image) {
Vec2f boxmin(width-1, height-1), boxmax(0, 0);
for (int i = 0; i < 3; i++) {
boxmin.x = std::min(boxmin.x, pts[i].x);
boxmax.x = std::max(boxmax.x, pts[i].x);
boxmin.y = std::min(boxmin.y, pts[i].y);
boxmax.y = std::max(boxmax.y, pts[i].y);
}
for (int x = boxmin.x; x <= boxmax.x; x++) {
for (int y = boxmin.y; y <= boxmax.y; y++) {
Vec3f P(x, y, 0);
Vec3f bc = barycentric(pts[0], pts[1], pts[2], P);
if (bc.x < 0 || bc.y < 0 || bc.z < 0) continue;
P.z = pts[0].z * bc.x + pts[1].z * bc.y + pts[2].z * bc.z;
// 计算到光源的距离
double dis = (world2screen(light) - P).norm();
if (zbuffer[P.x][P.y] < dis) { // 当前点远离光源终点, 更接近光源
zbuffer[P.x][P.y] = dis;
image.set(P.x, P.y, color);
}
}
}
}
void draw(vdd &zbuffer, Model *model, TGAImage &image, std::string filename) {
for (int i = 0; i < model->nfaces(); i++) {
std::vector<int> face = model->face(i);
std::vector<Vec3f> screen(3); // 存储图像坐标
std::vector<Vec3f> world(3); // 存储世界坐标
for (int j = 0; j < 3; j++) {
Vec3f tmp = model->vert(face[j]);
screen[j] = world2screen(tmp);
world[j] = tmp;
}
// 外积计算三角面的单位法向量
Vec3f n = ((world[2] - world[0]) ^ (world[1] - world[0])).normalize();
double intensity = n * light; // 内积计算光强
if (intensity < 0) continue; // 光强<0, 不进行绘制, 即背面裁剪
uint8_t c = 255 * intensity;
fill(screen, zbuffer, TGAColor(c, c, c), image);
}
image.write_tga_file(filename);
}
int main() {
Model *model = new Model("obj/african_head.obj");
// Model *model = new Model("obj/monster.obj");
TGAImage image(width, height, TGAImage::RGB);
vdd zbuffer(width, vd(height, -1e30));
light = Vec3f(0, 0, -1);
// light = Vec3f(-1, 0, -1).normalize();
draw(zbuffer, model, image, "output.tga");
delete model;
return 0;
}垂直光照


斜光照

