Perceptron Learning Algorithm 感知器算法 - 神经网络基础
感知器(英语:Perceptron)是Frank Rosenblatt在1957年就职于康奈尔航空实验室(Cornell Aeronautical Laboratory)时所发明的一种人工神经网络。它可以被视为一种最简单形式的前馈神经网络,是一种二元线性分类器。(From:Wiki-感知器)
感知器可以理解为神经网络中的一个“神经细胞”,在这里我们研究是最简单的神经网络问题,只有一个感知器的情况,而神经网络中则是由大量的感知器分层组合而成,问题更加复杂。我们先理解感知器学习原理以后,在回过头看它和神经网络的关系。
问题引入
问题:在 空间中,有 个离散点,分别为 ,它们被分为两种,一个点要么具有性质一,要么具有性质二,考虑如何使用一个超平面将这两种点分离开来,即一种类型的点尽可能多的在同一面。
下面通过一个二维的例子进一步理解这个问题。
我们考虑一个 空间中的分类问题,比如学生的上课时长和自主学习时长与是否可以通过某门课程的问题,如下图
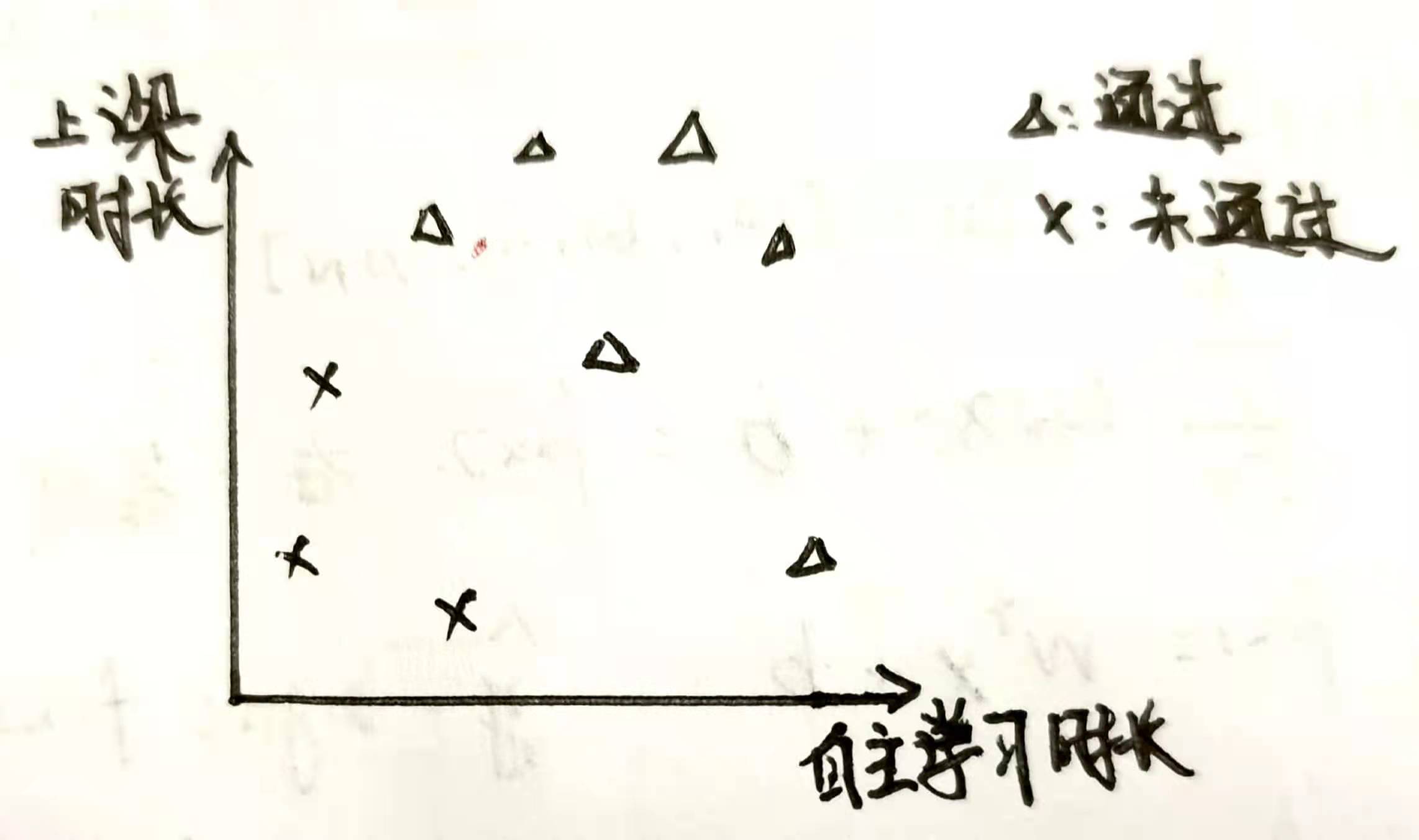
我们期望找到一条直线(二维中的超平面就是直线,三维为平面),使得这条直线将两种点区分开,所有的叉都在直线的下方,三角形都在直线的上方。比如
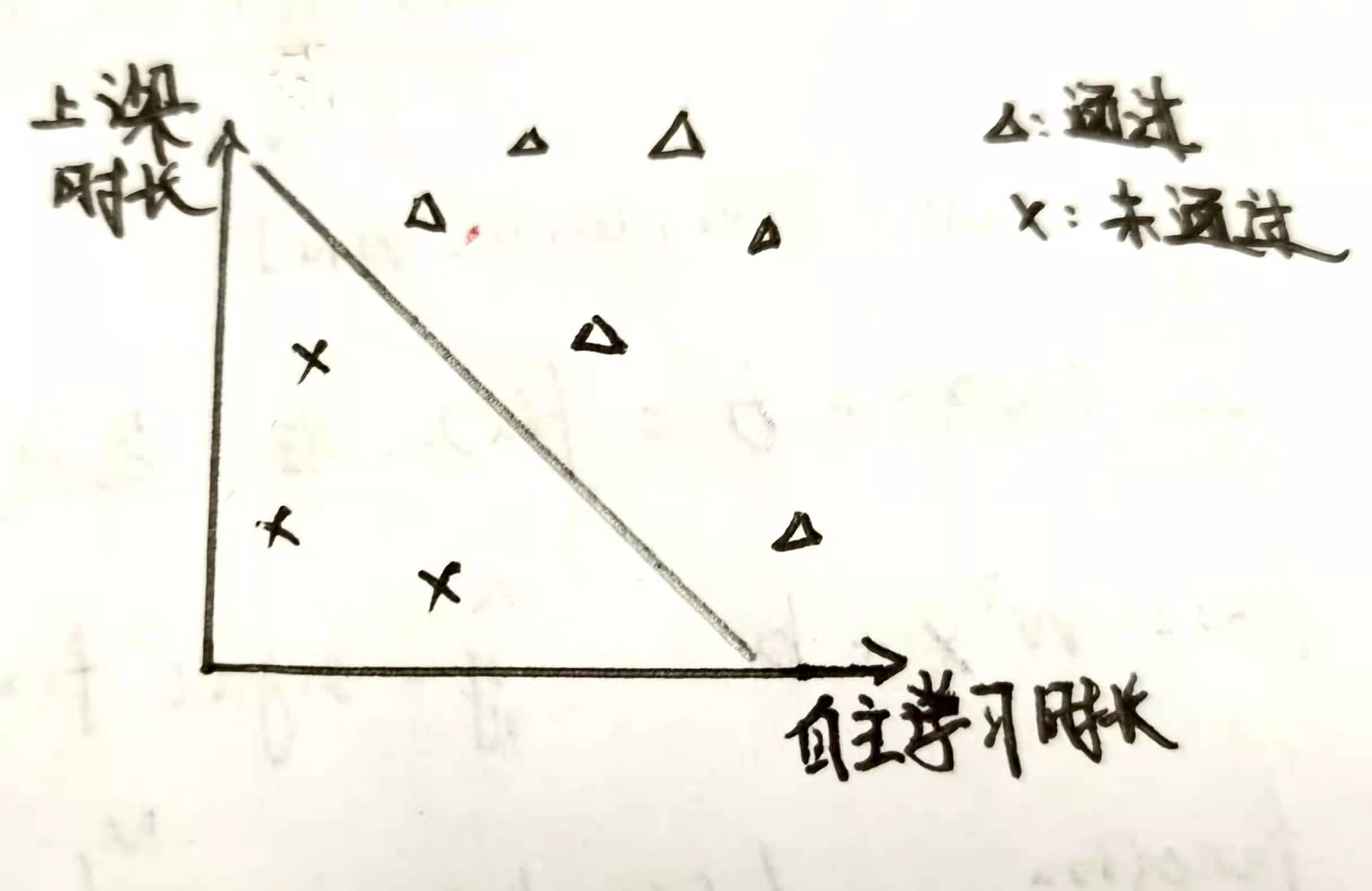
利用最小二乘法可以直接计算出最优解,但这里不进行讨论
一个很容易的想法是,随便给出一条直线,通过不断调整位置,不断改进,从而满足条件,比如现在随机给出一条直线如下图
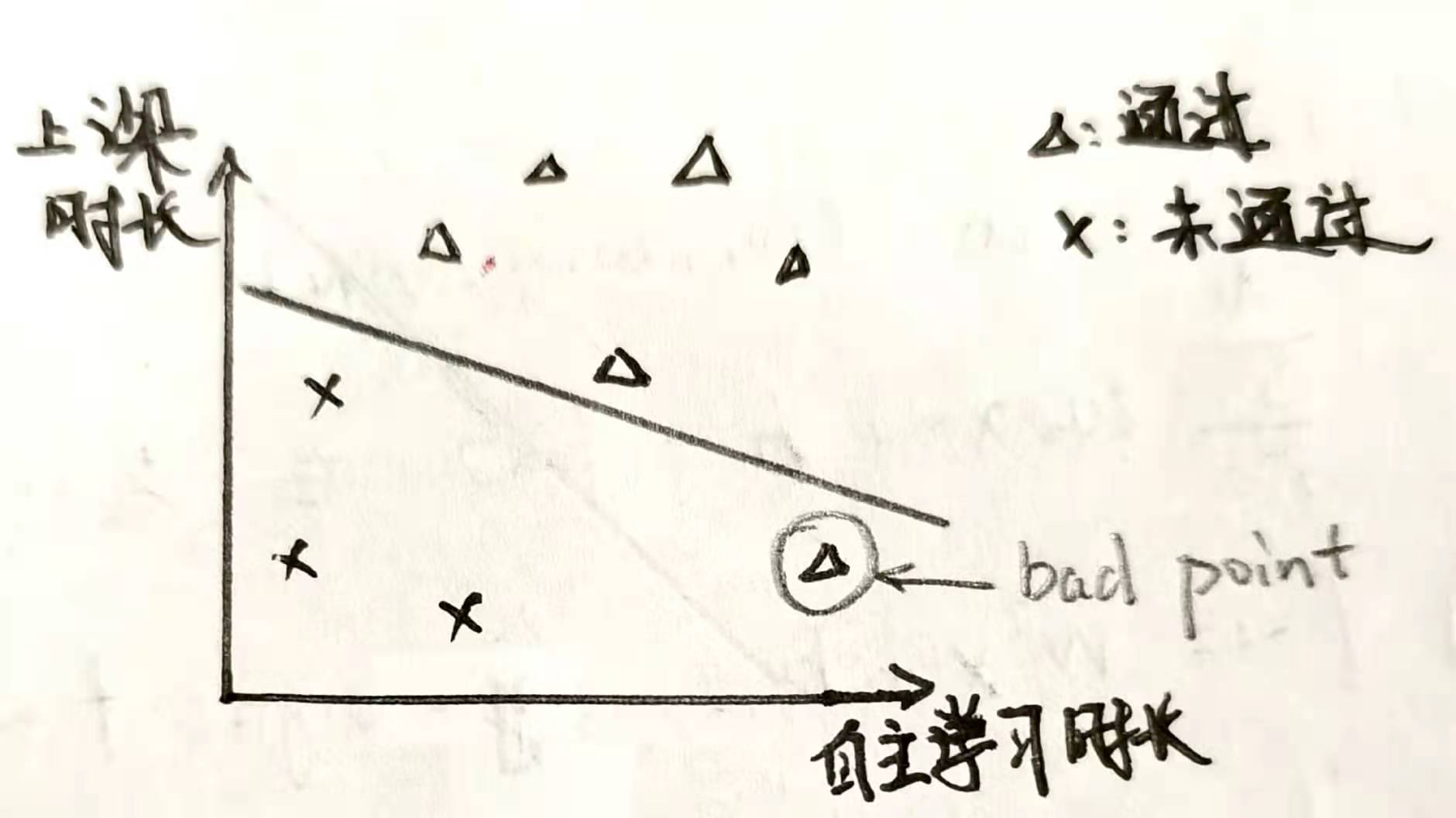
图中明显有一个三角形在直线的下方,那么应该如何调整这条直线,使得这个三角形调整到直线上方去呢?
数学模型
为了便于理解,全部的定义先在二维空间上进行,最后再推广到多维空间中
符号定义
我们将这个分类问题数学化,假设一共有 个点,点集合为
每个点都具有两种属性之一,现在考虑第 个点,将它的属性记为 ,则我们可以这样理解 :
接下来定义直线,我们知道二维的直线可以通过三个参数来定义:
做出如下定义:
则可以将直线写成向量乘积的形式:
所以对于一个点 ,代入当前直线方程 ,可得如下含义
我们发现,如果 和 同号,则说明该点在分类正确,否则需要对直线进行调整。
而且可以通过点到直线的距离表示当前点的权重,由几何知识可知,点 到直线 的距离可以表示为:
问题设计
对于这个问题,我们可以设计如下的一个最优化问题:
其中 是所有分类错误的点集合,即 。
它的含义是:考虑当前所有分类错误的点集合,由于 说明它当前分类错误,则需要修改曲线,则 应该增大,为了转化为最小值问题,需要在前面加上负号。 则表示当前点的权重对 的影响。由于 恒正,对于一次优化过程为常数,所以可以视为 ,于是最优化问题为:
随机梯度下降法
要使得 最小,就是使得每一个分类错误的点的 达到最小。下面我们考虑一个分类错误的点 ,记 ,考虑通过最速下降法使得 减小,即沿负梯度方向更新 ,使得 对于当前点 下降速度最快,具体方法如下,当前要最小化的函数为
其中 表示当前分类错误的点所具有的属性,所以
则,权向量 的更新方法为:
其中 为新的权向量, 为学习参数,当 较大时,每次更新对 的影响较大,变化速度较快,反之, 的变化速度较慢,参数 可以与很多变量相关,这里不进行深入讨论,直接将其取值为 。所以
如果只考虑单个分类错误的点对权向量 的修改,可能会导致其他分类正确的点变得分类错误,所以为了均摊每一个点对权向量的影响,每次从 中随机取出一个点,对 进行更新。
推广
不难发现,上述方法可以直接推广到 中,公式完全和二维形式相同,对向量定义稍加修改
对于每个分类错误的点 对 进行如下的更新即可
代码实现
使用 Jupyter Notebook 完成,源代码下载,可以直接使用VsCode查看。或者在Github上查看,Github传送门
import numpy as np
import numpy.random as nr
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = (12, 12) #固定图像大小
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号# 生成随机点
N = 100
xn = nr.rand(N, 2) # 第一列为横轴,第二列为纵轴
x = np.linspace(0, 1) # 选取[0,10]上的线性分布
# 选取一线性函数
# a, b = nr.rand(), nr.rand()
a, b = 0.8, 0.2
f = lambda x : a*x + b
#fig = plt.figure() # 创建图层
#figa = plt.gca() # get current axes 获取当前的坐标轴,处理坐标轴相关信息
plt.plot(x, f(x), 'tab:red')
dn = np.zeros([N, 1]) # 点在分割线上方为1,反之为-1
def print_base(xn, dn):
plt.plot(xn[:,0], xn[:,1], 'o', color='tab:blue') # 蓝色,圆点
for i in range(N):
if (f(xn[i, 0]) > xn[i, 1]): # 分割线下方
dn[i] = 1
plt.plot(xn[i, 0], xn[i, 1], 'o', color='tab:green')
else:
dn[i] = -1 # 分割线上方
print_base(xn, dn)
plt.legend(['上方', '分割线', '下方'])
plt.title('根据分割线选择点')
plt.show()
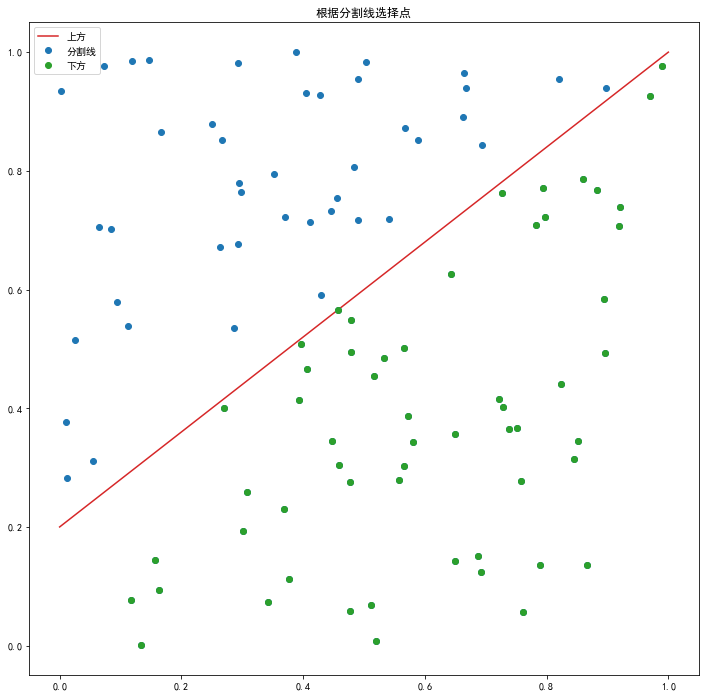
现在假设我们不知道这条分割线,只能根据这些点的位置和它们所具有的两种性质,找到一条直线将它们分为两半,这就是最简单的分类算法,下面用二维分类问题举例。
假设一个点坐标为,则可以记为为,这样方便写成直线的形式,记,则当前直线可以写为,假设当前的点的性质和不符合,即它本应该在下方但是它现在在上方,则我们希望通过改变参数旋转或平移直线,使得当前点的性质得以满足,将以上问题转化为下面这个优化问题:
具体解释可以看博客,通过最速下降法,即沿梯度方向更新,得到如下更新的方法:
其中为学习系数,即每次更新的权重,下面代码中直接取值为,通过代码运行可以看出迭代效果
def print_per(xn, dn, w): # 打印图像
if (w[2] == 0):
return
y = lambda x: -w[0]/w[2] - w[1]/w[2]*x
x = np.linspace(0, 1)
plt.plot(x, y(x), 'tab:blue')
print_base(xn, dn)
def perceptron(xn, dn, max_iter=10000, w=np.zeros(3)):
'''
二维分类问题
Input:
xn: 数据点,Nx2矩阵
dn: 分类标准,Nx1矩阵
max_iter: 最大迭代次数
w: 初始化参数矩阵
Output:
w: 迭代结果,最优分类曲线
'''
f = lambda x: np.sign(w[0] + w[1] * x[0] + w[2] * x[1]) #当前点x在f的上方则返回正数
now = 1
plt.figure(figsize=(10, 60))
chk = [10, 100, 500, 1000, 5000, 9999] #打印迭代过程中的图像
for _ in range(max_iter):
i = nr.randint(N) #随机取出一个点
if (_ in chk):
plt.subplot(6, 1, now)
plt.title('当前迭代次数'+str(_))
now += 1
print_per(xn, dn, w)
if (dn[i] != f(xn[i,:])): # 如果分类错误,则进行修正曲线
w[0] += dn[i]
w[1] += dn[i] * xn[i,0]
w[2] += dn[i] * xn[i,1]
plt.show()
return w
w = perceptron(xn, dn)

plt.figure();
print_base(xn, dn)
y = lambda x: -w[0]/w[2] - w[1]/w[2]*x
plt.plot(x,y(x),'b--',label='感知器求出的解')
plt.plot(x,f(x),'r',label='原始分割线')
plt.legend()
plt.title('比较原始分割线和求出的解')
plt.show()
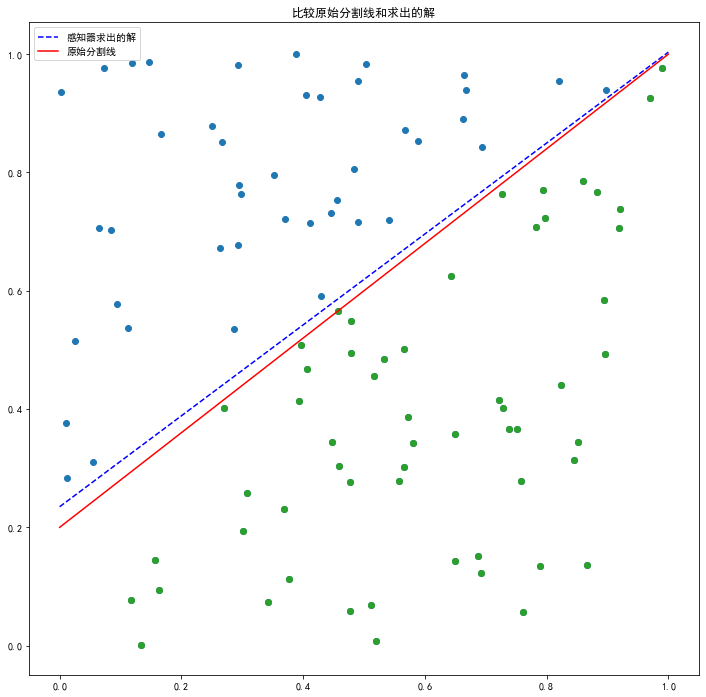
过拟合问题
如果我们将最大迭代次数 max_iter 调的过大,比如现在的 10000 就会发生过拟合问题,就是该曲线对于改组数据虽然能做到完美分类,但是并不一定能对新的数据有很好的的分类效果,所以最大迭代次数并不能调的太大,通过观察过程图像,可以发现其实迭代次数达到 1000 次的时候已经达到比较好的分类效果了。
过拟合问题在复杂的神经网络中会有更多的处理方法,留到以后接着讨论。
回顾算法
我们可以通过下图来清晰的理解感知器算法:
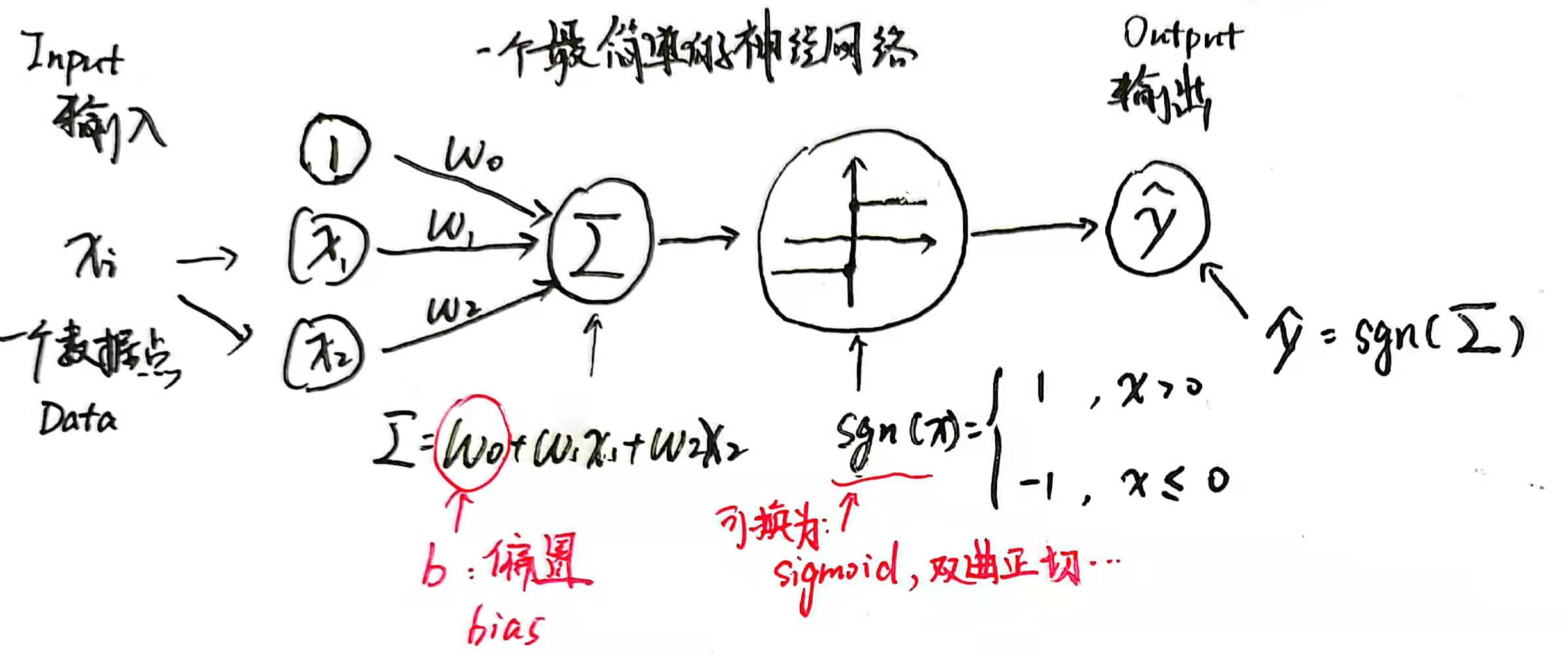
其中偏置(bias)是以后神经网络中常用的名词。整个算法的计算流程可以分为上图中的四步,先随机取出一个数据点,加权求和,通过一个正规化函数(这里是 ),然后输出;根据损失函数 的负梯度方向修正 ,这就是整个神经网络的工作原理。
为了能够完成更加复杂的分类问题,我们可以将这样的感知器堆叠在一起形成更复杂的神经网络,计算也变得更加复杂,但原理和一个感知器本质上没有任何区别,所以理解一个感知器的工作原理对后续神经网络的学习是十分有用的。
上文中python代码和markdown文件,可以直接在Github上查看下载,Github传送门
上文的算法没有参考某本具体的神经网络课本,只是通过视频学习和参考别人代码思路后自己总结的一些内容,如有错误请直接指出`(>﹏<)′