CTC Loss及OCR经典算法CRNN实现
这里我们将基于深度神经网络CNN+CTC loss进行OCR(图像文本识别),可以使用经典CRNN网络,但是我这里使用的是全卷积网络,因为文本长度并不长,所以并不想考虑文本的序列信息,没有使用LSTM部分。
参考文献:
- (CTC loss)Connectionist Temporal Classification: Labelling Unsegmented Sequence Data with Recurrent Neural Networks
- (CRNN)An End-to-End Trainable Neural Network for Image-based Sequence Recognition and Its Application to Scene Text Recognition
- YC Note - OCR:CRNN+CTC開源加詳細解析
- ZhiHu - jax:CTC loss 实作与优化
OCR检测
在OCR检测问题中,设数据集格式为 ,其中 表示输入的图像数据, 表示该图像对应的文本串,假设我们的图像长宽一定均为 的灰度图像。
注:此处的 表示的是已经通过目标检测出来的带有一行文字的图片框(如下所示),也就是说必须确保该图像中具有文字,目标检测技术可以使用YOLO,R-CNN,SDD等等。





设数据集中全体字符集大小为 (包含空字符,用于占位),考虑一个样本 ,设文本串 长度为 ,设深度神经网络为 ,于是我们可以利用卷积的平移等变性,将 的输出压缩成一个高度为 宽度为 的 维特征,于是输出中第 列特征,就正好代表原始图像 中,按照宽度平均划分为 份中的第 块的信息(这块信息大小也称为卷积的感受野范围)。
也就是说,如果我们图像中的文本正好就是横向排布的,而且只有一行,那么如果我们的 将原图划分的足够细,那么对于原图中第 个字符,,使得 表示的特征正好是该字符对应的,下图中的Feature Sequence就是 ,其中每个特征向量对应的感受野大小就是虚线所指向在图片中的框大小:
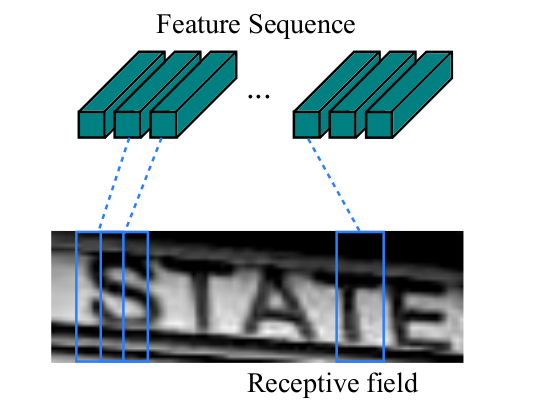
并且我们网络的输出 ,所以可以直接作用 后就是该处对应的字符概率分布,但是这里我们会很容易发现一个问题,我们的预测的特征数目 一定是大于字符长度 的,所以我们将会有非常多的空字符和重复字符(相近的感受野可能识别成同样的字符),举一个例子:
我们将空字符记为 ,假设标签为 ,则 ,一个训练好的模型的识别结果可能是
如果两个字符之间的间距过大则模型可能识别出多个空字符 ,如果字体过大或者文本特征非常明显,可能识别出重复的字符例如 ,那么我们就需要分别对上述两个问题进行解决,首先将连续出现的相同字符是保留一个,再将剩余的 全部去掉即可,我们将由大小为 的字符集构成的全体字符串集合记为 ,其中的字符串记为 ,将上述化简算子记为 。
容易发现一个小问题,如何识别 呢?这样重复出现的字符之间就必须预测出一个空字符,例如 。
模型预测方法
不基于字典的理论预测方法非常直接,枚举所有可能字符串 和所有可能的预测串 ,求出通过简化运算得到该串 的概率,取概率最大的一个即可:
但是实际上我们当然不可能枚举出所有的 和 ,所以简单来说可以通过贪心或者贪心树搜索来寻找,效果其实差不多,贪心就是直接取每个位置 出现概率最大的字符,然后通过简化运算即可得到预测结果。
训练方法
CTC Loss
该问题的难点在于如何训练,简单来说,我们只需要通过极大似然就可以对概率进行优化:
难点在于我们如何求出 ,这就是一个动态规划(DP)问题了:
首先我们将 中间隔插入 变为 ,例如 CAT 就变为 -C-A-T-,其中 - 表示 ,假设我们的预测的序列长度为 ,那么简化运算 生成的所有序列就是下面表格中从红色点开始,对于位置 ,只能向右移动到 或 或者当 时可以移动到 ,最终移动到蓝色点上,全体路径通过 运算均可以得到 CAT,又由于每条路径对应了一个概率,我们只需要考虑所有路径的概率和,就是我们要求的 了。
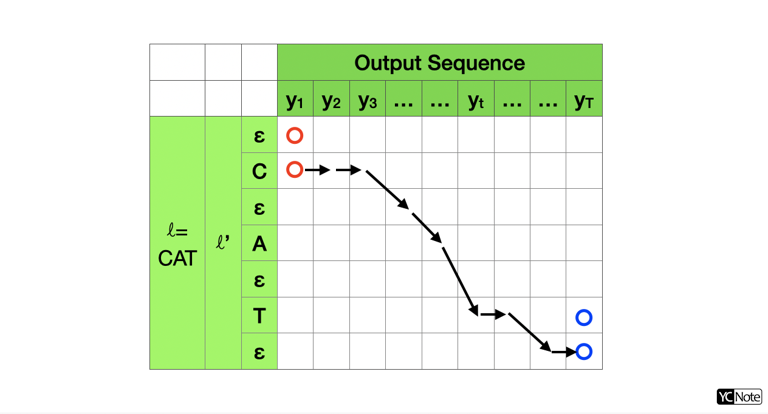
假设表格中 处的概率大小为 ,设状态 表示从任意一个起点到达 全部路径的概率之和,即
考虑点 的状态只能来自于 ,或者当前 且 时可以从 转移得到,则状态转移方程为
其中 只有当其中的条件判断为真时为 否则为 。
初始化:。
时间复杂度:,最终CTC损失函数
JAX 实现
但是,这里不是C++,不仅要正向求出损失函数,还需反向计算梯度,在论文和YC Note中介绍了如何计算反向梯度,于正向方法类似,也是利用DP。
但是现在自动微分技术这么强,并且能用GPU加速,不想这么麻烦。所以下面将利用JAX实现GPU加速的CTC损失计算:
首先要有JAX的基础,知道JAX中不能直接使用 if, for 这样会使得代码变得非常慢,常用的技巧是,用 mask 或者 jax.lax.cond 代替 if,用 jax.lax.scan 代替 for,参考 optax.ctc_loss 的代码设计方法(实际运用中推荐直接调用 optax.ctc_loss),我也自己重新实现了一遍,并且在小数据上速度略高于 optax.ctc_loss,这里具体对其原理进行解释:
我们先要将概率转化为 域下的运算,即做变换 ,这样可以避免浮点数的精度问题,在数值计算中我们还需要一个 ,用于表示概率为 (代码中取为 ),则原状态转移方程变化为:
将 的奇偶行分别提取出来:令,其中
那么 就表示到达原字符串 中点的概率大小, 表示到达空字符中点的概率大小,于是我们可以分别对他们俩进行求解:
其中
并且由红色表出的部分为二者共同的一项,只不过 计算中需要取去除掉重复的部分,所以我们可以先计算 中红色的项,然后补全重复的项就可以得到 了,部分代码如下:
def update_h(h, delta): # 错位加和
return jnp.logaddexp(
h,
jnp.pad(delta, ((0,0),(1,0)), constant_values=log_eps)
)
tmp = update_h(pre_log_h, pre_log_g + repeat * log_eps) # 上式中红色部分
log_g = jnp.logaddexp(pre_log_g, tmp[:,:-1]) + logprob_char
log_h = update_h(
tmp,
pre_log_g + (1.0 - repeat) * log_eps # 补全去除掉的部分
) + logprob_blank最后利用 jax.lax.scan 对 对应的维度进行遍历即可,初始化
还有一些小技巧,例如计算 用到了爱因斯坦求和约定 jnp.einsum:
logprobs = jax.nn.log_softmax(logits)
B, T, C = logits.shape
B, N = labels.shape
one_hot = jax.nn.one_hot(labels, C) # (B,N,C)
logprobs_char = jnp.einsum('btc,bnc->tbn', logprobs, one_hot) # (T,B,N)@jax.jit
def ctc_loss(logits, labels, blank_id=0, log_eps=-1e5):
logprobs = jax.nn.log_softmax(logits)
B, T, C = logits.shape
B, N = labels.shape
lens = jnp.max(jnp.where(labels!=0, jnp.arange(N)+1, 0), axis=-1) # (B,)
one_hot = jax.nn.one_hot(labels, C) # (B,N,C)
logprobs_char = jnp.einsum('btc,bnc->tbn', logprobs, one_hot) # (T,B,N)
logprobs_blank = jnp.transpose(logprobs[..., blank_id:blank_id+1], (1,0,2)) # (T,B,1)
pre_log_g = jnp.ones((B,N)) * log_eps
pre_log_h = jnp.ones((B,N+1)) * log_eps
pre_log_h = pre_log_h.at[:,0].set(0.0)
repeat = jnp.pad(labels[:,:-1] == labels[:,1:], ((0,0),(0,1))).astype(jnp.float32)
def update_h(h, delta):
return jnp.logaddexp(
h,
jnp.pad(delta, ((0,0),(1,0)), constant_values=log_eps)
)
def loop_func(pre, x):
pre_log_g, pre_log_h = pre
logprob_char, logprob_blank = x
tmp = update_h(pre_log_h, pre_log_g + repeat * log_eps)
log_g = jnp.logaddexp(pre_log_g, tmp[:,:-1]) + logprob_char
log_h = update_h(
tmp,
pre_log_g + (1.0 - repeat) * log_eps
) + logprob_blank
ret = (log_g, log_h)
return ret, ret
init = (pre_log_g, pre_log_h)
xs = (logprobs_char, logprobs_blank)
_, (log_g, log_h) = jax.lax.scan(loop_func, init, xs) # (T,B,N)
ans = update_h(log_h[-1], log_g[-1])
ans_mask = jax.nn.one_hot(lens, N+1) # (B,N+1)
per_loss = -jnp.einsum('bn,bn->b', ans, ans_mask)
return per_loss这份代码和 optax.ctc_loss 的唯一区别就在于更新 的方法,我这里使用的是 jnp.pad 然后做加法,而 optax.ctc_loss 中用的是 jnp.concatenate 对 [h[:,:1], jnp.logaddexp(h[:,1:], delta)] 进行拼接,使用 jnp.pad 在CPU上速度能快接近一倍,在GPU上速度仍有微小优化。
我在代码 ctc_loss.py 中对 optax.ctc_loss ,我写的 ctc_loss ,知乎上 jax:CTC loss 实作与优化 中两个版本的代码,还有PyTorch官方代码 torch.ctc_loss ,总共四个代码进行了速度比较,如果在CPU上跑JAX并无优势,速度反而慢了接近一倍,但是在GPU上,JAX速度比PyTorch能更快一倍,在实际训练中训练速度应该能够更快:

网络架构
CRNN顾名思义,就是将网络拆分成CNN和RNN两部分:
- CNN为Backbone部分,用于提取图像特征,由于我们的输入图像大小仅有 ,所以这部分使用的是VGG模型(卷积+最大池化),同样能保持较小的参数量。
- RNN为BiLSTM,假设我们的输入维度为 ,分别表示Batch大小、时间序列长度 和特征维度 ,两个LSTM分别按照维度 的正向和反向对 分别求出两个输出结果 ,,最后对每个 按照最后一个维度进行合并就得到了BiLSTM的输出 。简单来说就是创建了两个LSTM,分别对序列的特征进行了正向和反向的提取。
网络结构与论文所给出的基本一致,如下图所示:

这里右侧Shape是我后续加的,现实了左侧层输出的宽度和高度或者特征的维数,输入图像为灰度,宽度必须为 的倍数,常用宽度为 ,则输入尺度为 输出尺度为 ,其中 为不同字符的类别数目。做的一点改进在于将所有的激活函数换成了Mish,所有的卷积后都会跟上BatchNormalization。
代码实现
使用MJSynth数据集,该数据集共包含8919273个样本(但是我解压后损坏了29个图像),都是通过打印体字体进行数据增强来模仿真是环境中的各种字体,总共包含 种字符,英文大小写共 个,数字共 个。代码包括两部分:
- 数据集tfrecord转化及预处理:katacv/utils/ocr:
- 核心代码:katacv/ocr
cd KataCV
python katacv/utils/ocr/translate_tfrecord.py --path-dataset "your/mjsynth_path" # 创建tfreocrd文件到数据集同级目录下
python katacv/ocr/ocr_ctc.py --train --path-dataset-tfrecord "your/mjsynth_path/tfrecord" # 开始训练可以在 ocr_ctc.py 中加入 --wandb-track 参数使用 wandb 在线查看训练情况。模型训练参数可以在 katacv/ocr/constant.py 中进行修改,也可以通过 ocr_ctc.py
训练结果
训练上使用了cosine学习率调整,初始学习率为 ,训练20个epochs,batch size大小为 ,没有使用 正则项:训练结果 wandb-OCR CRNN
通过贪心方法对字符进行预测,则整个字符串完全对应的准确率分别为:
- 验证集准确率:。
- 训练集准确率:。