Scikit-Learn 常用函数及模型写法

Scikit-learn安装

pip install scikit-learn  # 基础包安装
pip install scikit-image  # 图像处理包

Scikit-Learn设计原则

参考论文API design for machine learning software: experiences from the scikit-learn project，这里给出Scikit-Learn的估计器模型一致具有的功能：

1. 估算：能够根据数据集对于某些参数进行估算的对象称为估算器. 估算通过 fit() 函数执行，参数为数据集（包含一个或两个参数，第二个参数可以为数据集标签）. 引导估算过程的其他参数称为超参数（可通过 *.strategy 查看），一般在构造实例时确定.

2. 转换：部分估算器可以转化数据集称为转换器（例如 imputer）. 转换通过 transform() 函数执行，参数为待转换的数据集，返回的是转换后的数据集. 所有转换器都支持更为方便的函数 fit_transform()，相当于先调用 fit() 再调用 transform() 函数.

3. 预测：部分估算器可以基于给定的数据进行预测称为预测器（例如 LinearRegression）. 预测通过 predict() 函数执行，参数为待预测的数据集，返回数据集对应的预测结果. 还有可以进行评估，score() 用于衡量给定测试集的预测质量（输入为特征和对应标签）.

4. 检查模型：所有估计的超参数可以通过公共实例变量访问 *.strategy，所有估计其的学习参数可以通过有下划线的后缀公共实例变量访问，例如*.statistics_.

5. 数据类型：Scikit-Learn中所有的数据集都会使用 Numpy 或者 SciPy 稀疏矩阵表示，超参数为Python字符串或者数字.

6. 搭建估算器：可通过对转化器后加上预测器创建一个 Pipline 估算器.

数据处理

划分数据集

基于固定的随机种子进行的抽样.

均匀抽样

设定随机种子进行均匀划分，train_test_split(df, test_size=0.2, random_state=42)：df为数据集，test_size为测试集比例，random_state为随机种子.

from sklearn.model_selection import train_test_split

train, test = train_test_split(df, test_size=0.2, random_state=42)

分层抽样

分层划分数据集，由于测试集需要代表整个数据集的整体信息，首先对数据特征进行层划分，在每一层中，我们希望都要有足够的信息来表示这种类别，表示该层的重要程度.

1. 首先利用 pd.cut() 对层进行划分，例如划分为 $[0, 1.5, 3, 4.5, 6, \infty]$ 这样 $5$ 段.

2. 再使用Scikit中的api函数实例化划分模型 split=StratifiedShuffleSplit(n_splits=1, test_size=0.2, random_state=42)：n_splits 表示划分的总数据集个数，test_size 为测试集占比，random_state 表示随机种子.

3. 最后通过迭代方式生成训练集与测试集：train_idx, test_idx = next(split.split(df, df['income_cat']))（由于只生成一个数据集，所以可以直接用next获取第一个迭代结果）

from sklearn.model_selection import StratifiedShuffleSplit

df['income_cat'] = pd.cut(df['median_income'], bins=[0., 1.5, 3., 4.5, 6., np.inf], labels=[1,2,3,4,5])  # 根据需要划分出层


split = StratifiedShuffleSplit(n_splits=1, test_size=0.2, random_state=42)
train_idx, test_idx = next(split.split(df, df['income_cat']))
strat_train = df.loc[train_idx]  # 分层抽样得到的训练集
strat_test = df.loc[test_idx]  # 分层抽样得到的训练集
for ds in (strat_train, strat_test):  # 最后删除用于分层的列income_cat
    ds.drop('income_cat', axis=1, inplace=True)

分层抽样与均匀抽象对于特定类别的抽样偏差（抽样偏差计算方法：$(sample - base) / base * 100$），这里以收入中位数进行划分为 $5$ 类，如左图所示，右图中的前三列为总体、分层、均匀每层的数据占比，右侧为分层、均匀的抽样偏差.

绘制直方图及计算偏差表格代码

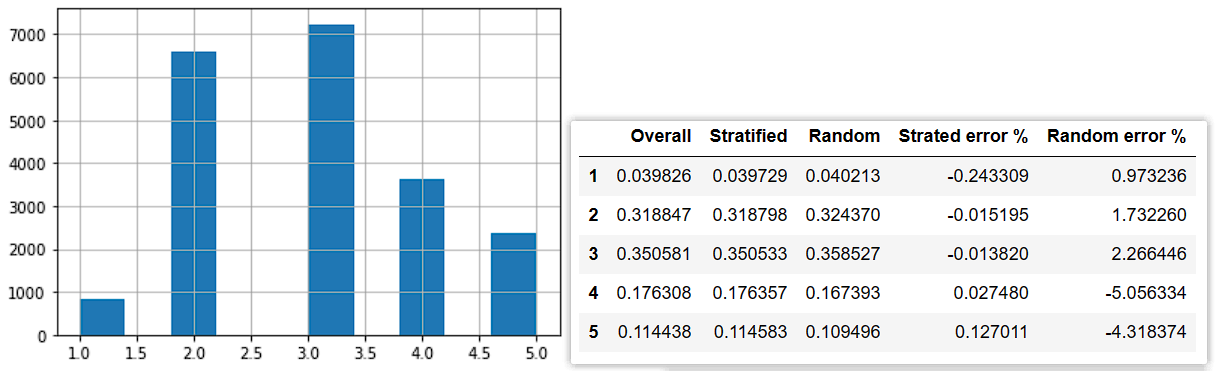
df['income_cat'].hist()  # 绘制直方图
plt.show()

base_income_ratio = df['income_cat'].value_counts() / len(df)  # 计算总体每层占比
strat_income_ratio = strat_test['income_cat'].value_counts() / len(strat_test)  # 计算分层抽样每层占比
test_income_cate = pd.cut(test['median_income'], bins=[0., 1.5, 3., 4.5, 6., np.inf], labels=[1,2,3,4,5])  # 计算均匀抽样的分层后标签
random_income_ratio = test_income_cate.value_counts() / len(test)  # 计算均匀抽样每层占比

# 计算误差表格
def calc_error(base, x):
    return (x - base) / base * 100
diff_test_sample = pd.concat([base_income_ratio, strat_income_ratio, random_income_ratio,
                              calc_error(base_income_ratio, strat_income_ratio),
                              calc_error(base_income_ratio, random_income_ratio)], axis=1)
diff_test_sample.columns = ['Overall', 'Stratified', 'Random', 'Strated error %', 'Random error %']
diff_test_sample = diff_test_sample.sort_index()
diff_test_sample  # 显示表格

转换器

主要使用Scikit-Learn中的转化器进行数据集转化，转化器介绍请见Scikit-Learn设计原则.

简易处理缺失值

使用 SimpleImputer 类对数据集中的缺失值进行填补（对每一列均进行相同的策略进行填补）. 填补策略 strategy 有 mean, median, most_frequent, constant（默认为 mean），当使用constant时会使用额外的参数 fill_value 进行填充.

# 使用Scikit-Learn中的方式进行填补
from sklearn.impute import SimpleImputer
imputer = SimpleImputer(strategy='median')  # 利用每列的中位数进行填补
df_num = df.drop('ocean_proximity', axis=1)  # 仅导入纯数字列
train_x = imputer.fit_transform(df_num)

print('填补策略:', imputer.strategy, '学习参数:', imputer.statistics_)

特征缩放

Scikit-Learn中的特征缩放相关类属于 sklearn.preprocessing，这里给出两个常用的缩放方法：

1. 归一化 MinMaxScaler，将数据集减去最小值后除以最大值，X = (X - np.min(X)) / np.max(X).

2. 标准化 StandardScaler，将数据集减去均值后除以标准差，X = (X - np.mean(X)) / np.std(X).

使用方法遵循转化器的使用方法，首先实例化，然后利用 .fit_transform(X) 对数据进行转化.

特征缩放类使用方法

from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import MinMaxScaler
std_scaler = StandardScaler()
mm_scaler = MinMaxScaler()
X = np.array(df_x[['housing_median_age']])

scale1 = std_scaler.fit_transform(X)  # 归一化
scale2 = mm_scaler.fit_transform(X)  # 标准化

自定义转换器

为了方便地使用Scikit-Learn功能（例如搭建 Pipline），自定义的转换器一般需要满足如下三种函数：fit(), transform(), fit_transform()，转换器中 fit() 可以直接返回 self.

还可以通过添加父类 sklearn.base.BaseEstimator 这个类可以在实例化的过程中确定的超参数（构造函数中必须给定具体参数名称，不能有*arg或**kargs）进行保存，便于后续查看 get_params() 或修改 set_params()；通过添加父类 sklearn.base.TransformerMixin 这个类可以自动生成 fit_transorm() 函数，无需自己重写.

---

这里以对原数据集的特征加入新的属性为例：

1. 每户平均所用房间数: rooms_per_households.

2. 每户平均人口数：population_per_households.

3. 每间房的平均卧室数：bedrooms_per_rooms. （可选是否添加）

由于原始数据为DataFrame格式，转化为numpy后无法通过列名进行查找，所以先要给定列名与索引的查找关系，所需列的索引编号分别有 total_rooms, total_bedrooms, population, households.

from sklearn.base import BaseEstimator, TransformerMixin

class CombinesAttributersAdder(BaseEstimator, TransformerMixin):
    def __init__(self, idxs, add_bedrooms_per_rooms=True):
        self.idxs = idxs
        self.add_bedrooms_per_rooms = add_bedrooms_per_rooms
    def fit(self, X, y=None):
        return self
    def transform(self, X):
        rooms_per_households = (X[:, self.idxs['total_rooms']] / X[:, self.idxs['households']]).reshape([-1,1])
        population_per_households = (X[:, self.idxs['population']] / X[:, self.idxs['households']]).reshape([-1,1])
        ret = [X, rooms_per_households, population_per_households]
        if self.add_bedrooms_per_rooms:
            ret.append((X[:, self.idxs['total_bedrooms']] / X[:, self.idxs['total_rooms']]).reshape([-1,1]))
        return np.concatenate(ret, axis=1)

idxs = dict([(col, i) for i, col in enumerate(df_x.columns)])  # 获取列名与索引的对应关系
attr_adder = CombinesAttributersAdder(idxs, add_bedrooms_per_rooms=False)
df_extra_attribs = attr_adder.fit_transform(df_x.values)

# 可以通过set_params()和get_params() 修改、查看超参数
attr_adder.set_params(add_bedrooms_per_rooms=False)
attr_adder.get_params()

编码器

文本转数字

使用 sklearn.preprocessing.OrdinalEncoder 转化器，每一个字符换转化为唯一对应的数字（从0开始）. 用法如下

from sklearn.preprocessing import OrdinalEncoder
df_cat = df_x[['ocean_proximity']]  # 数据集中 ocean_proximity 列为字符数据，注意使用切片，要使得结果为矩阵而不是向量
ordinal_encoder = OrdinalEncoder()
df_cat_encoded = ordinal_encoder.fit_transform(df_cat)  # df_cat为字符串数据集
# 注: df_cat.shape 应该为 (-1, 1) 的形式（即是矩阵而不是向量）

print(ordinal_encoder.categories_)  # 显示转换器转化的类别名称

用数字表示类别，相近的数字可能会使机器认为两种类别相近，但实则不然，所以引入one-hot表示方法.

文本转one-hot向量

one-hot向量本质就是将类别以仅含有0,1的向量形式表示出来，例如总类别数目为5个，若当前样本属于类别0，则它对应的one-hot向量为 [1,0,0,0,0]，即对应类别处为1，其他位置都是0.

使用 sklearn.preprocessing.OneHotEncoder 转化器可以很容易做到这点. 用法如下（转化结果为 SciPy 的稀疏矩阵形式，因为结果中有较多的 0，为了节省内存，使用稀疏矩阵仅保存 1 的位置，可通过 .toarray() 显示稀疏矩阵的内容）

使用 .categories_ 可以查看分类的名称.

加入 handle_unknown='ignore' 可以避免在transform中遇到了fit中未见过的类别（这种情况可能在OneHotEncoder在K-折交叉验证中出现）

from sklearn.preprocessing import OneHotEncoder
onehot_encoder = OneHotEncoder(handle_unknown='ignore')
df_cat_onehot = onehot_encoder.fit_transform(df_cat)

df_cat_onehot[:10].toarray()  # 显示前10行内容

数字编码与one-hot编码的对应关系

# 数字 <-> 稀疏矩阵
[[1.],     [[0., 1., 0., 0., 0.],
 [4.],      [0., 0., 0., 0., 1.],
 [1.],      [0., 1., 0., 0., 0.],
 [4.],      [0., 0., 0., 0., 1.],
 [0.],      [1., 0., 0., 0., 0.],
 [3.],      [0., 0., 0., 1., 0.],
 [0.],      [1., 0., 0., 0., 0.],
 [0.],      [1., 0., 0., 0., 0.],
 [0.],      [1., 0., 0., 0., 0.],
 [0.]]      [1., 0., 0., 0., 0.]]

转换流水线

最为方便的数据预处理做法就是将上述的转换器全部堆叠起来，成为流水线式的转换操作，称之为 Pipline.

在Scikit-Learn中 Pipline 是由一系列的转换器进行的堆叠（也就是必须要有 fit_transform() 函数），而堆叠的最后一个只需是一个估计器（也就是可以只有 fit() 函数），最后流水线也具有最后一个估计器的功能，如果最后一个估计器有 transform() 函数，那么流水线也有 fit_transform() 函数，如果最后一个估计器有 predict() 函数，那么流水线也具有 fit_predict() 函数.

通过 .named_steps 可以获得内部转换器模块，从而检查参数.

---

这里构造的流水线具有以下三个功能：

1. 数据缺失值处理（中位数填补）.

2. 属性值添加（自定义的转换器）.

3. 特征缩放（标准化转换器）.

Pipline 的构造函数包含一个元组列表，每个元组包含 (名称, 转化器)，第一个属性为转化器的名称，命名自定义（不包含双下划线，不能重复），第二个属性为转化器构造函数

from sklearn.pipeline import Pipeline

num_pipeline = Pipeline([
    ('imputer', SimpleImputer(strategy="median")),  # 转化器
    ('attribs_adder', CombinedAttributersAdder(idxs)),  # 转化器
    ('std_scaler', StandardScaler()),  # 仅需为估计器
])
df_num_tr = num_pipeline.fit_transform(df_num)

---

对不同列分别进行转换

由于原数据集中既有数字特征，也有文本特征，所以需要分别做预处理，sklearn.compose.ColumnTransformer 可以很好的完成这项操作. 它可以非常好的适配 DataFrame 数据类型，通过列索引找到需要处理的列，最后逇返回值，会根据最终矩阵的稠密度来判断是否使用稀疏矩阵还是密集矩阵（矩阵密度定义为非零值的占比，默认阈值为 sparse_threshold=0.3）

构造函数中，需要一个元组列表，每个元组包含 名称, 转化器, 列索引列表，名称同 Pipline 的要求（自定义，不重复，无双下划线），列索引列表可以直接为 DataFrame 中的列名.

通过 .named_transformers_ 可以获得内部转换器模块，从而检查参数.

from sklearn.compose import ColumnTransformer

# 从分层抽样后的训练数据中划分出特征与标签
df_x = strat_train.drop('median_house_value', axis=1)
df_num = df_x.drop('ocean_proximity', axis=1)  # 划分出纯数字特征，便于预处理
train_y = np.array(strat_train['median_house_value']).copy()  # 注意不要破坏原始数据集

num_attribs = list(df_num)  # numeral
cat_attribs = ['ocean_proximity']  # category

full_pipline = ColumnTransformer([
    ('num', num_pipeline, num_attribs),  # 将数字使用之前的pipline进行转化
    ('cat', OneHotEncoder(), cat_attribs),  # 将字符串转化为one-hot类别
])

train_x = full_pipline.fit_transform(df_x)

模型训练与评估

如果模型训练速度太慢，想看到训练进度可以在模型超参数设定处加入 verbose=1，就可以看到训练进度，verbose 数字越大数据越详细.

常用模型

多分类模型

一些严格的二元分类器（SVM，线性分类器）也可以用于分类，有以下两种策略可以通过多个二元分类器实现多分类的目的：（例如创建一个模型将数字图像分类为0到9）

1. 一对多(One vs Rest)：训练10个二元分类器，每种数字一个，用于区分是或不是该数字，例如一个分类器用于划分是数字0或不是数字0，最后取最高的分类器对特定数字的决策分数作为整个模型的预测结果.

2. 一对一(One vs One)：训练 $\binom{2}{10}=45$ 个二元分类器，每个分类器用于区分两种数字，例如区分0和1,0和2,1和2等等. 每个分类器得到一个预测结果，最后通过判断哪个类获胜最多作为模型的预测结果.

可以查看官方文档得到分类器对于多分类的实现方法.

线性模型

线性回归

1. sklearn.linear_model.LinearRegression 使用SVD分解求解线性模型（适合小数据量，复杂度约为 $\mathcal{O}(n^2)$），lin_reg.intercept_ 返回截距（偏置项），lin_reg.coef_ 返回各个特征属性值的对应系数.

from sklearn.linear_model import LinearRegression

lin_reg = LinearRegression()
lin_reg.fit(train_x, train_y)  # 模型估计

x = train_x[:5]  # 测试部分训练数据
y = train_y[:5]
print("Predictions:", lin_reg.predict(x))  # 预测结果
print("Labels", list(y))  # 真实结果

2. sklearn.linear_model.SGDRegressor(max_iter=1000, loss='squared_error', penalty='l2', alpha=0.0001, learning_rate, eta0, random_state, l1_ratio) 使用随机梯度下降法求解线性模型（适合大数据量），使用均方误差损失函数，正则项默认使用参数的 $\ell_2$ 范数，正则化系数为 alpha，eta0 为初始学习率，学习率默认使用随迭代次数增加而递降的动态形式，递降策略由 learning_rate 控制，最大迭代次数为 max_iter，随机种子为 random_state，当正则项为弹性网络时，l1_ratio 为 l1 范数的占比.

from sklearn.linear_model import SGDRegressor

sgd_reg = SGDRegressor(max_iter=1000, penalty=None, eta0=0.1, random_state=42)
sgd_reg.fit(X, y)

多项式回归

from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures

polynomial_pipeline = Pipeline([
    ("poly_features", PolynomialFeatures(degree=2, include_bias=False)),  # 使用最高为二次多项式，构造特征之间的关系
    ("std_scaler", StandardScaler()),  # 记得标准化特征
    ("lin_reg", LinearRegression())  # 最后用线性回归训练
])
polynomial_pipeline.fit(X, y)

Logistic回归

使用 sklearn.linear_model.LogisticRegression(C) 实现Logistic回归，默认使用 $l_2$ 正则化项，正则化系数为 $1/C$，如果不想使用正则化，可将 $C$ 设置为较大值.

from sklearn.linear_model import LogisticRegression

log_reg = LogisticRegression(random_state=42)
log_reg.fit(X, y)

Softmax回归

也是使用 sklearn.linear_model.LogisticRegression(multi_class='multinomial')，只需将 multi_class 设置为 multinomial 即可使用Softmax回归求解多分类任务（否则可能使用“一对多(OvR)”分类策略）

from sklearn.linear_model import LogisticRegression

log_reg = LogisticRegression(multi_class='multinomial', C=10, random_state=42)
log_reg.fit(X, y)

随机梯度下降优化SVM

适用于大数据训练，初始参数默认为 loss='hinge', max_iter=1000，可以设定随机种子 random_state.

from sklearn.linear_model import SGDClassifier

sgd_clf = SGDClassifier(random_state=42)
sgd_clf.fit(train_x, train_y)

绘制PR曲线

混淆矩阵，精度，召回率定义请见混淆矩阵-定义.

SGD 模型输出的是对样本的打分，而判断是否属于哪类则是通过阈值来确定的，默认阈值为 0，对于二分类问题，阈值与召回率成负相关关系（因为如果将所有都预测为真，则召回率一定很好），我们可以根据不同的阈值从而获得不同的预测结果，对应不同的模型，从而绘制出精度与召回率的关系图.

首先需要求出模型对每个样本的打分，还是用过 cross_val_predict 获得，但是这里需要从模型的 decision_function 获得评分，而不是最后的预测结果，使用 method 可以选择最后模型输出的函数，默认为 method='predict'.

最后使用 sklearn.metrics.precision_recall_curve 不同阈值下的精度与召回率的值，使用方法为

• precision_recall_curve(y_true, probas_pred)，第一个参数为标签真实值，第二个参数为所有可能的得分. 于是阈值会根据全部得分从小到大逐一选择，并求出对应精度与召回率. 返回值：精度，召回率，阈值.

注意：精度和召回率的维数为 (n_thresholds + 1,) 比阈值大1，精度最后一个元素为 1，而召回率最后一个元素为 0，绘图时记得将其删去.

from sklearn.metrics import precision_recall_curve
from sklearn.metrics import auc

train_y_scores = cross_val_predict(sgd_clf, train_x, train_y_5, cv=3, method='decision_function')
precisions, recalls, thresholds = precision_recall_curve(train_y_5, train_y_scores)

def plot_precision_recall_vs_threshold(precisions, recalls, thresholds):
    plt.figure(figsize=(10, 5))
    plt.plot(thresholds, precisions[:-1], "b--", label="精度")
    plt.plot(thresholds, recalls[:-1], "g-", label="召回率")
    plt.legend()
    plt.xlabel("阈值")
    plt.axis([thresholds.min(), thresholds.max(), 0, 1.05])
plot_precision_recall_vs_threshold(precisions, recalls, thresholds)
plt.show()

def plot_precision_vs_recall(precisions, recalls):
    plt.figure(figsize=(6, 6))
    plt.plot(recalls, precisions, 'r-', lw=2)
    plt.xlabel('召回率(Recall)')
    plt.ylabel('精度(Precision)')
    plt.axis([0, 1, 0, 1])
    plt.title('P-R曲线')
plot_precision_vs_recall(precisions, recalls)
plt.show()
print("曲线下面积为:", auc(recalls, precisions))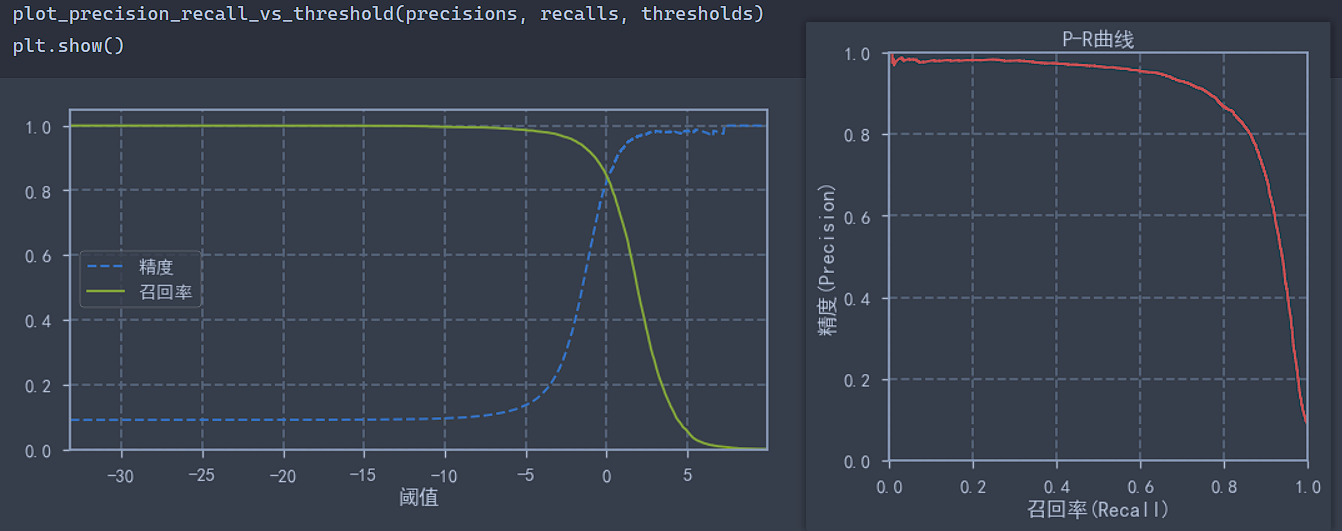

绘制ROC曲线

ROC曲线的定义请见 PR曲线与ROC曲线.

使用 sklearn.metrics.roc_curve 获得 fpr, tpr, theresholds 对应结果（与 precision_recall_curve 曲线返回值相同）

注：由于有 drop_intermediatebool=True 参数，会自动舍弃一些次优阈值，使得曲线显示更加平滑（个人认为是求了凸包后的结果），所以返回结果中阈值个数可能远小于输入的样本个数.

使用 sklearn.metrics.roc_auc_score 还可以非常方便的求出ROC曲线的曲线下面积AUC.

from sklearn.metrics import roc_curve
from sklearn.metrics import roc_auc_score

fpr, tpr, thresholds = roc_curve(train_y_5, train_y_scores)
print("ROC得分:", roc_auc_score(train_y_5, train_y_scores))

def plot_roc_curve(fpr, tpr, label=None):
    plt.figure(figsize=(8, 6))
    plt.plot(fpr, tpr, lw=2)
    plt.plot([0, 1], [0, 1], 'k--')
    plt.axis([0, 1, 0, 1])
    plt.xlabel('FPR（1-特异度）')
    plt.ylabel('TPR（召回率）')
plot_roc_curve(fpr, tpr, label='SGD')
plt.show()
print("ROC得分:", auc(fpr, tpr))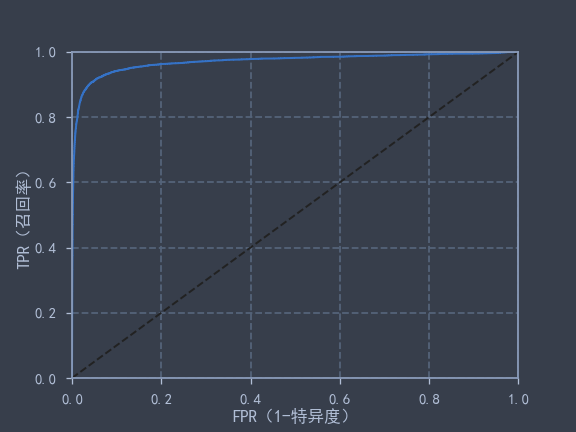

决策树

from sklearn.tree import DecisionTreeRegressor

tree_reg = DecisionTreeRegressor()
tree_reg.fit(train_x, train_y)

K近邻

回归

一个有效的方法是用于对图像进行降噪处理，以MNIST数据集为例.

# 生成随机噪声图像
import numpy as np
np.random.seed(42)
noise = np.random.randint(0, 100, (len(train_x), 784)) / 255
train_x_modify = train_x + noise
noise = np.random.randint(0, 100, (len(test_x), 784)) / 255
test_x_modify = test_x + noise
train_y_modify = train_x
test_y_modify = test_x

使用 sklearn.neighbors.KNeighborsRegressor 即可获得K近邻回归模型，并选取一些图像进行预测，显示图像的函数请见 常用命令 - Matplotlib 同时绘制多个图像 中的 plot_figures.

from sklearn.neighbors import KNeighborsRegressor

knn_reg = KNeighborsRegressor()
knn_reg.fit(train_x_modify, train_y_modify)

some_idx = [0, 4, 6, 10]
sample_x_modify = test_x_modify[some_idx]
sample_y_modify = test_y_modify[some_idx]

clean_image = knn_reg.predict(sample_x_modify)
plot_figures(np.concatenate([(sample_x_modify[i], sample_y_modify[i], clean_image[i]) for i in range(len(some_idx))]), images_per_row=3)

下图中第一列为噪声图像，第二列为原图像，第三列为降噪后效果.

随机森林

回归模型

from sklearn.ensemble import RandomForestRegressor

# 可以设定随机种子；训练速度比较慢，有些时候可以查看训练进度
forest_reg = RandomForestRegressor(random_state=42, verbose=1)
forest_reg.fit(train_x, train_y)

# 随机森林模型还有每种类别的重要性分数
feature_importances = rand_search.best_estimator_.feature_importances_
# 进一步我们可以获得每种类别的重要度排名
extra_attribs = ['rooms_per_households', 'popultion_per_households', 'bedrooms_per_rooms']  # 额外加入的属性
cat_encoder = full_pipline.named_transformers_['cat']  # 获取字符串编码器的类别名
cat_attribs = list(cat_encoder.categories_[0])  # 字符串类别名
attributes = list(df_num) + extra_attribs + cat_attribs
sorted(zip(feature_importances, attributes), reverse=True)  # 对每种类别与对应的名称一并进行排名

分类模型

使用 .predict_proba 可以获得预测的概率分布.

获取预测得分：当分类问题是二分类时，通过 cross_val_predict 获得预测的概率分布，然后将正例列切片作为得分.

通过得分可以绘制ROC曲线图，参考SGD模型绘制ROC曲线，随机森林与SGD的ROC曲线对比.

from sklearn.ensemble import RandomForestClassifier

forest_clf = RandomForestClassifier(random_state=42)
forest_clf.fit(train_x, train_y)

# 获取预测概率分布
y_probas_forest = cross_val_predict(forest_clf, train_x, train_y, cv=3, method='predict_proba')
# 做正例切片作为得分
y_scores_forest = y_probas_forest[:, 1]
# 可以绘制ROC曲线图，计算ROC评分
fpr_forest, tpr_forest, thresholds_forest = roc_curve(train_y, y_scores_forest)
print("随机森林ROC评分:", roc_auc_score(train_y, y_scores_forest))

模型评估

交叉验证

一种简单的方法是使用 train_test_split 将训练集进一步划分为较小的训练集和验证集，然后使用较小的数据集进行训练，并在验证集上进行评估.

另一种方便的做法是使用Scikit-Learn中的K-折交叉验证功能 sklearn.model_selection.cross_val_score，假设 $K=10$，则具体做法是将训练集随机划分为10个不同的子集，每个子集称为一个折叠，对模型进行10次训练与评估——每次选取1个折叠作为验证集，剩余9个折叠作为训练集，返回一个包含10次评分的数组，评分规则可以在 scoring 属性中设定.

cross_val_score(model, train_x, train_y, scoring=make_scorer(mean_squared_error), cv=10)：待检验模型 model，训练集特征 train_x，训练集标签 train_y，scoring 打分标准（这里使用均方误差 mean_squared_error，还需要一个得分转化器，或者直接使用 neg_mean_squared_error 但返回的是负的均方误差)，cv 为划分的折叠个数为.

如果训练速度太慢，可以在模型构建处加入 verbose 参数，数字越大数据越详细.

from sklearn.model_selection import cross_val_score
from sklearn.metrics import make_scorer, mean_squared_error

scores = cross_val_score(model, train_x, train_y, scoring=make_scorer(mean_squared_error), cv=10)

自定义K-折交叉验证

通过 sklearn.model_selection.StratifiedKFold 实现自定义的K-折交叉验证，使用方法和 cross_val_score() 类似，只不过这里将折叠数参数记为 n_splits（默认为5），如果要保持相同的随机结果需要加入固定随机种子 random_state 并令 shuffle=True.

下面以一个二分类器为例：

from sklearn.model_selection import StratifiedKFold
from sklearn.base import clone

skfolds = StratifiedKFold(n_splits=3, random_state=42, shuffle=True)

for train_idx, test_idx in skfolds.split(train_x, train_y):
    clone_clf = clone(sgd_clf)  # 每次新创建一个模型
    train_x_folds = train_x[train_idx]
    train_y_folds = train_y[train_idx]
    test_x_folds = train_x[test_idx]
    test_y_folds = train_y[test_idx]

    clone_clf.fit(train_x_folds, train_y_folds)
    pred = clone_clf.predict(test_x_folds)
    accuracy = sum(pred == test_y_folds)
    print(accuracy / len(pred))  # 输出准确率

均方误差

在回归问题中，可以利用 sklearn.metrics.mean_squared_error 可以计算训练数据集上的均方误差MSE，另一个常用的是开更号后的结果RMSE.

from sklearn.metrics import mean_squared_error

mse = mean_squared_error(train_y, model.predict(train_x))
rmse = np.sqrt(mse)
# 可用 mean_squared_error(train_y, model.predict(train_x), squared=False) 直接计算RMSE

混淆矩阵

定义

混淆矩阵的列是真实值，行是预测值，$(i,j)$ 处的值表示真实值为 $i$ 时，模型预测结果为 $j$ 的个数.

在二分类的混淆矩阵的每个元素都有对应的名称：假设真实值与预测结果的列表排列均为 [假, 真]，则每个位置的元素对应名称如下所示：

• (1,1) 表示真负类(TN).
• (1,2) 表示假正类(FP).
• (2,1) 表示假负类(FN).
• (2,2) 表示真正类(TP).

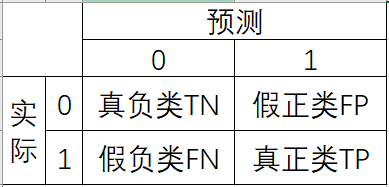
记忆方法非常简单，名称中第一个“真与假”表示是否预测正确，第二个“正与负”表示预测结果的类别.

有两个常用参数：

$$\text{精度} = \frac{TP}{TP+FP},\qquad \text{召回率} = \frac{TP}{TP+FN}$$

• 精度(Precision)：预测结果是真的时候，有多大概率是对的.
• 召回率(Recall)：标签为真的时候，能有多大的概率预测对.（如果用假设检验的第一类错误来理解，设原假设为样本标签为真，那么“1-召回率”就是第一类错误）

一种评估精度与召回率的方法是 $F_1$ 参数（两者的调和平均数）：

$$F_1 = \frac{2}{\frac{1}{\text{精度}}+\frac{1}{\text{召回率}}}$$

用法：使用F1一般是希望精度与召回率同时较高时所用，但是对于特定问题，可能仅需要某一种参数越高越好. 例如检测小偷，肯定希望召回率越高越好，也就是所谓的“宁可错杀一千，不可放过一个”；而视频筛选中，希望精度越高越好，因为我们希望即使错筛了很多好的视频，但是留下来的都是好的就行.

PR曲线与ROC曲线

精度-召回率曲线：模型通过得分是否超过阈值判断样本属于的类别，通过设定不同的阈值，从而可以得到不同的PR值，绘制出的曲线，一般称为PR曲线，一般也用PR曲线与x轴围成的面积(Area Under Curve, AUC)评估模型好坏（越大越好），面积计算可以使用 sklearn.metrics.auc. 具体实现请见 SGD模型绘制PR曲线.

---

另一种常用的曲线称为 受试者工作特征曲线(Receiver Operating Characteristic Curve, ROC)，绘制的是真正类率（TPR，召回率）和假正类率（FPR）的关系，而TPR就是之前定义的召回率，而FPR与特异度(TNR)定义相关，它们的定义如下

$$\text{假正类率FPR} = \frac{FP}{TN+FP},\\ \textbf{真负类率TNR(特异度)} = 1-FPR = \frac{TN}{TN+FP}$$

不难发现，这种什么什么率就是按照混淆矩阵的行占比来定义的，例如上述两个FPR和TNR就分别是全部负类样本中被错误预测的概率的和被正确预测的概率，特别的TNR还被称为特异度.

实际使用中，我们会直接画出ROC曲线，然后用曲线下面积AUC来评判模型的好坏. 具体实现请见 SGD模型绘制ROC曲线

实现

使用 sklearn.metrics.confusion_matrix(true_y, pred_y) 可以很容易地获得混淆矩阵. 而获得预测值的很好的一个方法是通过交叉验证返回的预测结果 sklearn.model_selection.cross_val_predict. 由于只使用了训练集，使用交叉验证可以保证将训练集进一步划分为更小的训练集与验证集，保证了预测的干净（预测数据没有再训练中出现）

from sklearn.model_selection import cross_val_predict
from sklearn.metrics import confusion_matrix

train_y_pred = cross_val_predict(sgd_clf, train_x, train_y, cv=3)
confusion_matrix(train_y, train_y_pred)

Scikit-Learn中可以很容易地计算出精度，召回率和 $F_1$ 参数，分别为 sklearn.metrics 中的 precision_score, recall_score, f1_score，代入预测值与真实值即可计算出结果.

from sklearn.metrics import precision_score, recall_score, f1_score
print("精度:", precision_score(train_y, train_y_pred))
print("召回率:", recall_score(train_y, train_y_pred))
print("F1:", f1_score(train_y, train_y_pred))

可视化

下面以MNIST数据集为例，使用 SGDClassifier 模型进行预测，通过 plt.matshow 绘制混淆矩阵图像，并绘制对应的每种类别的错误率.

train_y_pred = cross_val_predict(sgd_clf, train_x, train_y, cv=3)
confuse_matrix = confusion_matrix(train_y, train_y_pred)
plt.matshow(confuse_matrix, cmap='gray')
plt.show()

row_sums = conf_mx.sum(axis=1)
norm_confuse_matrix = confuse_matrix / row_sums
np.fill_diagonal(norm_confuse_matrix, 0)
plt.matshow(norm_confuse_matrix, cmap='gray')
plt.show()  # 可以看出，3很容易被分类成5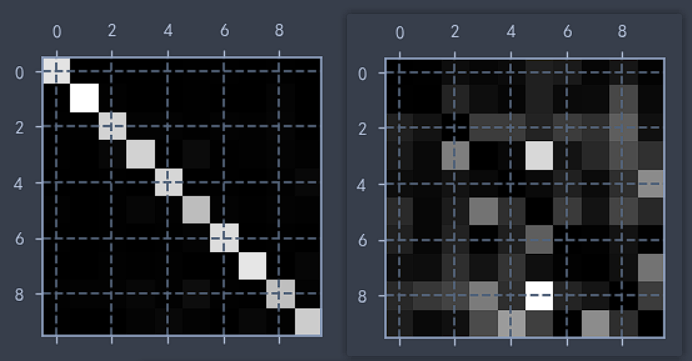

通过 常用命令 - Matplotlib 同时绘制多个图像 中的 plot_figures 对错误率较高的图像（3与5）绘制混淆矩阵实例图.

cl_a, cl_b = 3, 5  # class a and class b
aa_x = train_x[(train_y == cl_a) & (train_y_pred == cl_a)]
ab_x = train_x[(train_y == cl_a) & (train_y_pred == cl_b)]
ba_x = train_x[(train_y == cl_b) & (train_y_pred == cl_a)]
bb_x = train_x[(train_y == cl_b) & (train_y_pred == cl_b)]
plt.figure(figsize=(6, 6))
plt.subplot(221); plot_figures(aa_x[:25], images_per_row=5)
plt.subplot(222); plot_figures(ab_x[:25], images_per_row=5)
plt.subplot(223); plot_figures(ba_x[:25], images_per_row=5)
plt.subplot(224); plot_figures(bb_x[:25], images_per_row=5)
plt.show()

模型微调

在通过交叉验证确定了有效的模型后，对其参数进行进一步微调.

网格搜索

通过Scikit-Learn的 sklearn.model_selection.GridSearchCV 可以方便的尝试模型不同给定的参数组合，其会在不同的参数组合下进行交叉验证，所以也有 cv 参数设置，交叉验证的打分结果默认为越大越好，所以是参数是负的均方误差 neg_mean_squared_error.

• return_train_score=True 可以返回模型在训练集上的打分（一般用于判断模型的过拟合程度）.
• verbose=2 可以看到具体算到第几个折叠了.

使用GridSearchCV自动探寻超参数：基于 complete_pipline 和双下划线 __ 可以修改内部估计器的超参数. 这也就是不能用双下划线命名的原因.

这里建议将 error_score='raise' 参数进行设置，这样可以当输出值为 nan 时报出错误，从而便于调试错误的估计器.（有时候非常有用）

这里以随机森林的网格搜索为例.

from sklearn.model_selection import GridSearchCV
from sklearn.ensemble import RandomForestRegressor

params_grid = [  # 总共进行12+6=18次评估
    {'n_estimators': [3, 10, 30], 'max_features': [2, 4, 6, 8]},  # 第一个评估组合，3x4=12
    {'bootstrap': [False], 'n_estimators': [3, 10], 'max_features': [2, 3, 4]},  # 第二个评估组合，2x3=6
]
forest_reg = RandomForestRegressor(random_state=42)

grid_search = GridSearchCV(forest_reg, params_grid, cv=5, scoring='neg_mean_squared_error', return_train_score=True, verbose=2, error_score='raise')
grid_search.fit(train_x, train_y)  # 进行搜索

# 输出搜索到的最好参数组合
print(grid_search.best_params_)

# 输出不同参数对应的均值RMSE
cvres = grid_search.cv_results_
for mean_score, params in zip(cvres['mean_test_score'], cvres['params']):
    print(np.sqrt(-mean_score), params)

# 显示交叉验证全部结果（数据较多，用表格方便查看）
pd.DataFrame(grid_search.cv_results_)

随机搜索

通过 sklearn.model_selection.RandomizedSearchCV 可以方便的尝试各种随机参数组合，用法和 GridSearchCV 类似，只是多了两个属性：迭代搜索次数 n_iter 和随机种子random_state.

通过 scipy.stats.randint 可以随机产生一定范围内的整数，便于尝试不同组合.（可以先用网格搜索找到参数的大致区间，然后再用随机搜索找更优的参数组合）

from sklearn.model_selection import RandomizedSearchCV
from scipy.stats import randint

params_distri = [  # 参数分布
    {'n_estimators': randint(3, 30), 'max_features': randint(2, 8)},
]
forest_reg = RandomForestRegressor(random_state=42)

rand_search = RandomizedSearchCV(forest_reg, params_distri, cv=5, n_iter=20, random_state=42,  # 随机搜索20次
                                 scoring='neg_mean_squared_error', return_train_score=True, verbose=2)
rand_search.fit(train_x, train_y)  # 进行搜索

# 输出最好的组合及得分
print("参数组合:", rand_search.best_params_)
print("得分:", np.sqrt(-rand_search.best_score_))

# 尝试过的组合及对应的打分
cvres = rand_search.cv_results_
for mean_score, params in zip(cvres['mean_test_score'], cvres['params']):
    print(np.sqrt(-mean_score), params)

模型保存

Scikit-Learn训练好的模型可以通过 joblib.dump(model, 'model_name.pkl') 非常方便的保存，载入只需 joblib.load('model_name.pkl') 即可.

模型保存方法

import joblib

joblib.dump(model, "model.pkl")
model_loaded = joblib.load("model.pkl")