用JAX复现基于Transformer的miniGPT模型

参考文献：Atteetion Is All You Need $^{[1]}$ , On Layer Normalization in the Transformer Architecture $^{[2]}$ , Improving Language Understanding by Generative Pre-Training $^{[3]}$
参考Blog：The Illustrated Transformer - Jay Alammar
参考Code：minGPT-pytorch, decision-transformer, tinyGPT-jax

概述

Transformer 由论文[1]提出，这篇文章的核心框架就是 Self-Attention 和 Multi-Head Attention 架构，基于 Multi-Head Attention 本文给出了 Transformer 的 Encoder-Decoder 架构，但是当前流行的 GPT 模型只使用 Decoder 部分。首先我们将分析 Attention 部分，再分析 GPT1 模型的架构，最后在小文本数据集上进行训练，并可以进行简单句子扩写。

模型介绍

前置芝士

首先简单介绍 NLP 任务的前置芝士，Token 表示对文字的 $D$ 维编码，不同语言 Token 的对象不同：中文一般为一个字，英文可以是一个单词、也可以是一个阿拉伯字母，每个单词或者字母都有其对应的 $D$ 维编码。在 NLP 任务中，输入样本的维度一般为 $\mathbb{R}^{B\times T\times D}$ ，其中 $B$ 表示 Batch Size 大小， $T$ 表示 Token 数量， $D$ 表示对每个 Token 进行编码后的维度。（不失一般性，我们下面讨论的时候都省略第一个维度 $B$ ）

对字母进行编码 (Embedding) 成 $D$ 维 Token 就是一个 hash 过程，假设我们的字符集大小为 $N$ ，通过创建一个 $\mathbb{R}^{N\times D}$ 矩阵 $W = \{w_1,w_2,\cdots,w_N\}^T$ ，则字符集中第 $i$ 个字符的对应 Token 就是 $W_i$ 。在机器学习中，该编码矩阵 $W$ 可以在梯度下降中自动更新，无需自己手动设定。

Self-Attention 机制

Self-Attention 是一种自监督机制（此处也成为交叉注意力机制 Cross-Attention），本质上就是一种基于协方差矩阵对另一个向量进行加权平均的结果。定义如下：（默认声明 $w_i$ 表示矩阵 $W$ 的第一个维度中的第 $i$ 个元素）

设 $Q, K \in \mathbb{R}^{T\times d_k}, V\in\mathbb{R}^{T\times d_v}$ 分别表示第 $i$ 个 Token 的询问值 $q_i$ (Query)，键 $k_i$ (Key) 和值 $v_i$ (Value)，其中我们用 $\langle q_i, k_j\rangle$ 衡量第 $i$ 个 Query 与第 $j$ 个 Key 的相关性大小，我们想要求出每个 Query 对所有的 Key 计算平均后，对 Value 进行加权求和得到的结果，该过程可以表示如下：

z_i = \sum_{j=1}^{T}\text{softmax}(\{\langle q_i, k_l\rangle\}_{l=1}^{T})_j\cdot v_j

写成矩阵形式如下：

Z = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V,\qquad \text{其中softmax作用在最后一个维度上}

在这里 $1/\sqrt{d_k}$ 的原因： $\forall i\in \{1,\cdots, T\}$ 有 $q_{ij},k_{ij}\sim \mathcal{N}(0,\sigma^2), (j = 1,\cdots, d_k)$ ，则 $\sum_{j=1}^{d_k}q_{ij}k_{ij}\sim \mathcal{N}(0,d_k\sigma^4)$ ，由于 $\sigma\approx 1$ ，所以系数 $1/\sqrt{d_k}$ 可以保持输出的方差在 $1$ 左右，避免发散。

Self-Attention

注意力矩阵的修正

Causal Self-Attention（因果自注意力机制）：这里 $\Sigma:=QK^T$ 就是协方差矩阵（注意力矩阵），可以被用来衡量两组随机变量的相关性，其中 $\Sigma_{ij}$ 表示第 $i$ 个 Query 和第 $j$ 个 Key 之间的相关性大小，如果我们只期望每个 token 只考虑它及它前面的相关性，我们只需要令 $\Sigma_{ij}=0, (i>j)$ （只保留下三角部分，其余部分用 $0$ 替代）。通过这样变换后的协方差矩阵作用在 $V$ 上得到的结果就是因果注意力机制的输出。

文本续写：在文本续写时候，我们输入的文本 Token 数量通常会小于最大 Token 数量 $T$ ，我们就需要用 $0$ 对输入进行填充，即 $x = \{x_1,\cdots, x_t, 0,\cdots, 0\}^T$ ，那么我们在计算协方差矩阵时候就不要对填充部分计算相关性，即令 $\Sigma_{ij} = 0, (i>t, j>t)$

那么什么是自注意力中的自从哪来？我们还没有介绍 $Q,K,V$ 如何获得，假设我们输入的样本维度为 $x\in\mathbb{R}^{T\times D}$ ，有意思的是自监督中的三个值就是通过三个全连接 $W^{Q},W^{K}\in\mathbb{R}^{T\times d_k}, W^{V}\in\mathbb{R}^{T\times d_v}$ 分别输出得到的，即 $Q = xW^{Q}, K = xW^{K}, V = xW^{V}$ 。综上，自注意力机制表示如下：

\text{Attn}(x; W^{Q},W^{K},W^{V}) = \text{softmax}\left(\frac{xW^Q(W^K)^Tx^T}{\sqrt{d_k}}\right)(xW^V)

所以说模型到底是怎么理解 $Q,K,V$ 的真实含义其实我们无法知道，Query,Key,Value 这只是我们赋予其的概念。

排列等变性

设变换 $T: X\in\mathbb{R}^{N}\to Y\in\mathbb{R}^{N}$ ， $\forall x\in X$ ，对于任意的排列变换 $p: \mathcal{I}_{n}\to\mathcal{I}_{n}$ ， $\mathcal{I}_n$ 表示大小为 $n$ 的指标集（排列变换满足 $p(x) = p(x_1,x_2,\cdots,x_N) = (x_{i_1},x_{i_2},\cdots,x_{i_N}), (i_j\neq i_k, i_j,i_k\in\{1,\cdots, N\})$ ），若有 $T(p(x)) = p(T(x))$ 则称变换 $T$ 具有排列等变性。（简单来说就是把输入 $x$ 的下标重新排列下，再经过 $T$ 变换后的结果 $T(p(x))$ ，和直接把 $x$ 经过 $T$ 变换后再进行相同重新排列 $p(T(x))$ 结果一致）

下面我们证明 $\text{Attn}(p(x)) = p(\text{Attn}(x))$ ，设 $X\in \mathbb{R}^{L\times d} = (x_1,\cdots,x_L)^T$ ，忽略掉 softmax 和 $1/\sqrt{d_k}$ 系数，我们可以得到自注意力变换为 $XW^Q(W^K)^TX^TXW^V$ ，由于最后的 $W^V$ 是对第二维度进行变换的矩阵，满足对第一维度的排列等变性，简化为 $f(X) = XAX^TXB$ ，只需证 $f$ 具有排列等变性。由于

f(X) = XAX^TXB = \begin{bmatrix}x_1^T\\\vdots\\x_L^T\end{bmatrix}A\begin{bmatrix}x_1&\cdots&x_T\end{bmatrix}\begin{bmatrix}x_1^T\\\vdots\\x_L^T\end{bmatrix} = \begin{bmatrix} x_1^T\\\vdots\\x_L^T \end{bmatrix}A\sum_{i=1}^Lx_ix_i^T

注意到 $A\sum_{i=1}^Lx_ix_i^T$ 是与排列变换无关的常量，当我们将输入 $X$ 中的 $i,j$ 行交换后，输出的 $i, j$ 行也会相应进行交换，所以变换 $f$ 具有排列等变性。 QED

形象理解：由于自注意力是对 Query 进行的查询，当 Query 位置发生变换时，自注意力输出的结果也会相应发生变换。上式中的体现：结果中最左边的 $x$ 唯一确定输出的行排列顺序，而这个 $x$ 也同时确定 Query 的位置。

位置信息嵌入 (Position Embedding)

正是由于自注意力机制关于排列具有不变性，也即每个 Token 的位置信息无法被模型获取，所以我们传入样本 $x$ 时候，需要嵌入位置信息 $\text{PE}\in\mathbb{R}^{T\times D}$ ，其中 $\text{PE}_{i}$ 表示处于当前输入中第 $i$ 个 Token 的位置信息编码，我们可以将其直接加到传入样本上： $x\gets x + \text{PE}$ ，从而引入位置信息。

在论文[1]中是一个 $\text{PE}$ 由 $sin, cos$ 交错形成的固定矩阵（位置和频率相关），而更通用的做法则是将 $\text{PE}$ 作为可学习参数，让模型自己学习得到（初始化为全零）。

Multihead-Attention 模型

多头注意力模型（Multihead-Attention）就是将 Self-Attention 进行堆叠得到的，我们将上面的自注意力过程简记为 $\text{Attn}(x)$ ，设自注意力头数目为 $h\in \mathbb{N}_{+}$ ，则 Multi-Attention 过程表示如下：

\text{Multi}(x) = \left[\overset{h}{\underset{i=1}\text{Concate}}(\text{Attn}_i(x))\right]W^0\in \mathbb{R}^{T\times d_e}

其中 $\text{Concate}(W_1,W_2,\cdots,W_n)$ 表示将矩阵 $W_i$ 按照最后一个维度进行连接， $W^0\in \mathbb{R}^{(hd_v)\times d_e}$ ，其中 $d_e$ 表示 Multi-Attention 最终输出的每个 Token 的编码 (Embed) 维度。

Multihead-Attention

代码实现

Multihead-Attention 的代码实现上需要注意一下细节：

一般有 $h$ 能够整除 $d_e$ ，即 $h | d_e$ 且 $d_v = d_k = d_e / h$ ，所以我们无需定义 $d_v,d_k$ 。
可以将计算 $Q,V,K$ 的三个神经网络合为一个大网络，输出维度为 $3d_e$ ，将输出的结果先按照 $h$ 头数目进行划分，再将最后特征维度平均划分为三个维度为 $d_e / h$ 的 $Q,K,V$ 。
在计算完自注意力矩阵后需要通过一个 Dropout，避免过拟合。

# JAX 实现的 Causal Self-Attention 的多头注意力模型
class CausalSelfAttention(nn.Module):
  n_embd: int  # 表示 d_e NOTE: n_embd % n_head == 0
  n_head: int  # 表示 h
  p_drop_attn: float

  @nn.compact
  def __call__(self, x: jnp.ndarray, train: bool, mask_len: int = None):
    D = self.n_embd // self.n_head  # d_k = d_v
    B, L, _ = x.shape  # Bachsize, Token长度, Token特征维度
    mask = jnp.tri(L)  # Causal Self-Attention 中每个 Query 只考虑在其位置之前的 Key
    if mask_len is not None:  # 将大于 mask_len 的相关性设置为 0
      mask = jnp.where(jnp.arange(L).reshape(L, 1) >= mask_len, 0, mask)

    x = nn.Dense(3 * self.n_embd)(x)  # 统一计算 Q, K, V
    q, k, v = jnp.array_split(x.reshape(B, L, self.n_head, -1).transpose(0, 2, 1, 3), 3, -1)  # (B, h, L, D)
    attn = q @ jnp.swapaxes(k, -1, -2) / jnp.sqrt(D)  # (B, h, L, L)
    attn = jnp.where(mask == 0, -1e18, attn)  # 基于mask重置相关性矩阵，由于要作用softmax所以给的是-inf
    attn = jax.nn.softmax(attn)
    attn = nn.Dropout(self.p_drop_attn)(attn, deterministic=not train)
    y = (attn @ v).transpose(0, 2, 1, 3).reshape(B, L, self.n_embd)  # (B, L, n_embd)
    y = nn.Dense(self.n_embd)(y)  # (B, L, n_embd)
    return y

Transformer Block (Transformer Layer)

Transformer Block (Transformer Layer)就是一种带有残差连接和 Layer Normalization 的 Attention 架构，在论文中介绍了两种 Layer Norm 的放置位置，如下图所示：

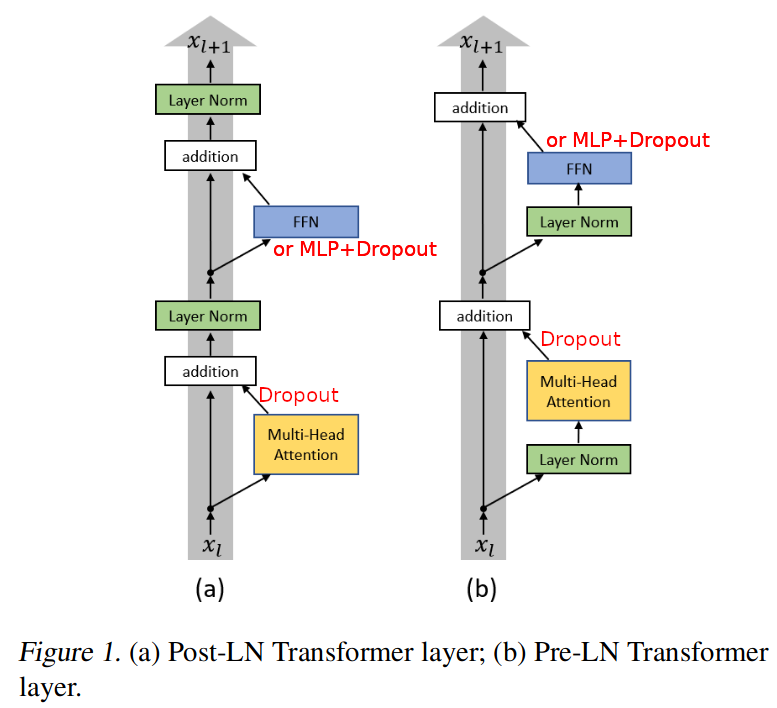
Transformer Layer

左图为论文[1]中所提出的原始 Transformer Layer 结构，右图为该论文给出将 Layer Norm 前置的结构，通过实验验证了前置的效果优于后置的。这里的残差连接和 ResNet 理念一致，因为一个 Transformer 模型需要非常多的 Transformer Block (Transformer Layer)，残差连接就是为了深度提升的同时保持原始特征不丢失。

后置 Layer Norm 的 JAX 代码实现如下：

# 定义一个 GPT 模型所需的参数配置
class GPTConfig(MainCLS):
  n_embd = 768
  n_head = 12  # Multihead个数
  n_block = 12  # Attention Block个数
  p_drop_embd = 0.1  # Embedding 后的 Dropout 比率
  p_drop_resid = 0.1  # 每次残差连接前的 Dropout 比率
  p_drop_attn = 0.1  # Attention计算完Softmax后的 Dropout 比率

  def __init__(self, n_vocab, n_token, **kwargs):
    self.n_vocab = n_vocab  # 词库大小（用于对输入的x进行Embedding）
    self.n_token = n_token  # Token的最大数目（训练时填满，预测时未填满时补零，并令 mask_len 为输入字符长度）
    for k, v in kwargs.items():
      setattr(self, k, v)
    assert self.n_embd % self.n_head == 0, "n_embd must be devided by n_head"

class TransformerBlock(nn.Module):
  cfg: GPTConfig

  @nn.compact
  def __call__(self, x: jnp.ndarray, train: bool, mask_len: int = None):
    attn_cfg = {key: getattr(self.cfg, key) for key in ['n_embd', 'n_head', 'p_drop_attn']}
    # 第一个残差连接 Multihead-Attention
    z = nn.LayerNorm()(x)
    z = CausalSelfAttention(**attn_cfg)(z, train, mask_len)
    x = x + nn.Dropout(self.cfg.p_drop_resid)(z, deterministic=not train)
    # 第二个残差连接 MLP 两层全连接: n_e -> 4n_e -> n_e
    z = nn.Sequential([
      nn.LayerNorm(),
      nn.Dense(4*self.cfg.n_embd), nn.selu,
      nn.Dense(self.cfg.n_embd),
    ])(x)
    x = x + nn.Dropout(self.cfg.p_drop_resid)(z, deterministic=not train)
    return x

GPT模型

在论文[1]中最开始提出的是一种Encoder-Decoder的形式，而论文[3]中给出的GPT-1模型则是只用Decoder进行编码，方法非常简单，只需将 Transformer Block 进行堆叠，最后连接一个全连接网络以及Softmax给出每个 Token 的下一个 Token 预测。例如训练集中有“我很好。”这句话，那么输入 $x$ 可以为“我很好”的编码，维度为 $\mathbb{R}^{3\times d_e}$ ，模型的预测目标为“很好。”，然而模型需要给出对每个 Token 的下一个 Token 的概率分布预测，也就是从整个词库中选出下一个词，即输出维度为 $\mathbb{R}^{3\times n_v}$ ，其中 $n_v$ 表示整个词库大小。

从代码上理解非常容易：

class GPT(nn.Module):
  cfg: GPTConfig

  @nn.compact  # x: (B, L, Nv)
  def __call__(self, x: jnp.ndarray, train: bool, mask_len: int = None):
    cfg = self.cfg
    # 为位置编码 pos_embd 创建一个可学习变量，下面两种创建方法结果一致
    pos_embd = self.param('pos_embd', lambda _, shape: jnp.zeros(shape), (1, cfg.n_token, cfg.n_embd))  # 直接声明新的变量
    # 或者 pos_embd = jnp.expand_dims(nn.Embed(cfg.n_token, cfg.n_embd)(jnp.arange(cfg.n_token)), 0)  # 通过 nn.Embed 创建相同的变量，注意需要在Batch维度扩展
    x = pos_embd + nn.Embed(cfg.n_vocab, cfg.n_embd)(x)  # (B, L, n_e)
    x = nn.Dropout(cfg.p_drop_embd)(x, deterministic=not train)
    for _ in range(cfg.n_block):
      x = TransformerBlock(cfg)(x, train, mask_len)
    x = nn.LayerNorm()(x)
    x = nn.Dense(cfg.n_vocab)(x)  # 预测的对数概率形式
    return x

模型训练及预测代码可以见下文（用JAX实现，PyTorch实现类似）。

模型训练

def model_step(state: TrainState, x: jnp.ndarray, y: jnp.ndarray, train: bool):
  dropout_rng, base_rng = jax.random.split(state.dropout_rng)  # 创建 dropout 随机种子
  def loss_fn(params):
    logits = state.apply_fn({'params': params}, x, train=train, rngs={'dropout': dropout_rng})  # (B, L, n_vocab)
    tmp = -jax.nn.log_softmax(logits).reshape(-1, logits.shape[-1])  # 计算对数概率 (BxL, n_vocab)
    loss = tmp[jnp.arange(tmp.shape[0]), y.reshape(-1)].mean()  # 根据target计算cross-softmax损失
    acc = (jnp.argmax(logits, -1).reshape(-1) == y.reshape(-1)).mean()  # 计算准确率
    return loss, acc
  (loss, acc), grads = jax.value_and_grad(loss_fn, has_aux=True)(state.params)  # 求导
  state = state.apply_gradients(grads=grads)  # 更新梯度
  state = state.replace(dropout_rng=base_rng)  # 更新随机种子
  return state, (loss, acc)

模型预测

def predict(state: TrainState, x: jnp.ndarray, rng: jax.Array, mask_len: int = None):
  logits = state.apply_fn({'params': state.params}, x, train=False, mask_len=mask_len)
  if mask_len is not None:  # 之取出最后一个我们所关心的预测值
    logits = logits[jnp.arange(logits.shape[0]), mask_len-1, :]  # (B, n_vocab)
  pred = jax.random.categorical(rng, logits, -1)  # 使用 gumbel 概率进行离散采样
  return pred

简单文本训练

数据集搭建

训练数据集来自 tinyGPT-jax，文本包含四大名著以及几篇莎士比亚的文章，这里我采用 torch.utils.data.Dataset 做数据读入，值得注意的是数据集划分方式（文本数据集不像图像数据集直接随机采样就行，文本还要求每个样本的字符保持连续性），由于数据量非常小，所以我们可以将全部文本字符串读入到内存中，存储到字符串 text 中，简单起见，我们将每个 token 定义为一个中文字符和一个阿拉伯字母（而非一个英文单词）。

设整个文本数据集大小为 $N$ ，训练集与验证集大小占比为 $(1-r):r$ ，我们首先将其平均划分为 $n_d$ 块，每块大小为 $n_c = \left\lfloor\frac{N}{n_d}\right\rfloor$ ，然后再将每个块中的前 $(1-r)n_c$ 个字符划分给训练集，后面剩余的字符划分给验证集。

text = ...  # 全部文本数据
data = self.encode(text)  # 将文本对应为非负整数索引
block_size = len(data) // n_divide  # 块大小
train_block_size = int(block_size * (1 - val_ratio))  # 每个块中的训练集大小
self.data = {  # 划分数据集
  'train': np.concatenate([data[i:i+train_block_size] for i in range(0, len(data), block_size)]),
  'val': np.concatenate([data[i+train_block_size:i+block_size] for i in range(0, len(data), block_size)])
}

我们的数据集大小为 $8650026$ ，词库大小为 $5840$ ，划分的训练集大小为 $6920026$ ，验证集大小为 $1730000$ ，如果把每个字符开始的一段句子都作为样本进行训练，大约要 $(6920026-128)/64 \times 0.37 \approx 11 \text{hours}$ （在 RTX4060-Laptop 上训练一个 batch_size=64, n_token=128 的时间为 0.37s）。

所以为了简短时间，我将每个训练集大小设置为 $512\times 128$ 个 Token 也就是训练 $512\times 0.37\approx 3 \text{mins}$ ，验证集大小设置为 $32\times 128$ 个 Token 也就是训练 $10 \text{seconds}$ 左右，而 Token 的开始位置就是从对应的数据集中随机采样获取。具体实现如下：

class TextDataset(Dataset):
  def __init__(self, data, n_token, datasize):
    # 文本数据集（以转为非负整数索引），一个样本的Token数量，随机采样的数据集大小
    self.data, self.n_token, self.datasize = data, n_token, datasize
  
  def __len__(self):
    return self.datasize
  
  def __getitem__(self, idx):
    idx = random.randint(0, len(self.data) - 2 - self.n_token)  # 随机获取一个Token开始的采样点
    d = self.data[idx:idx+self.n_token+1]  # 获取一个长度为n_token的样本
    x, y = d[:self.n_token], d[1:]  # 构建input与target
    return x, y

代码框架

源代码中包含5个代码文件：

ckpt_manager.py  # 使用orbax对模型参数进行管理
dataset.py  # 使用torch.utils.data.Dataset和DataLoader读取数据集
miniGPT.py  # 使用flax搭建GPT-1模型
predict.py  # 模型预测，通过读取模型参数进行文本续写
train.py  # 模型训练（支持Tensorboard记录训练曲线，wandb上传）

使用方法：直接运行 train.py 等待训练完成（RTX 4060 Laptop）WandB训练结果。

predict.py 执行效果：

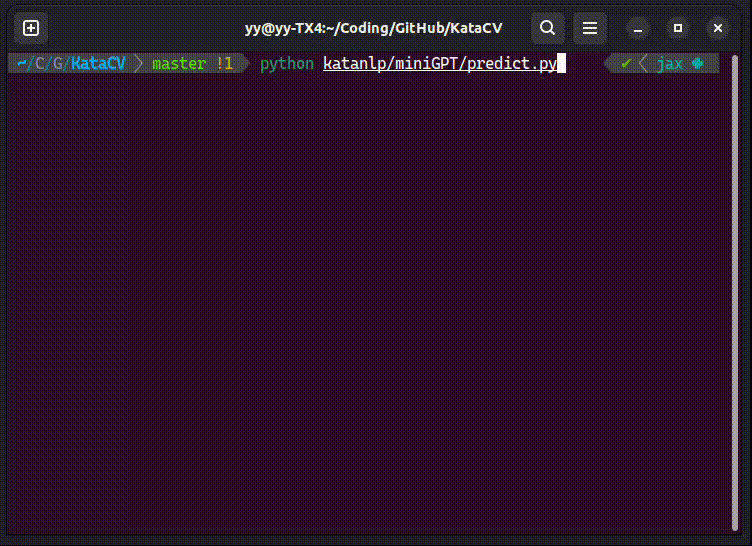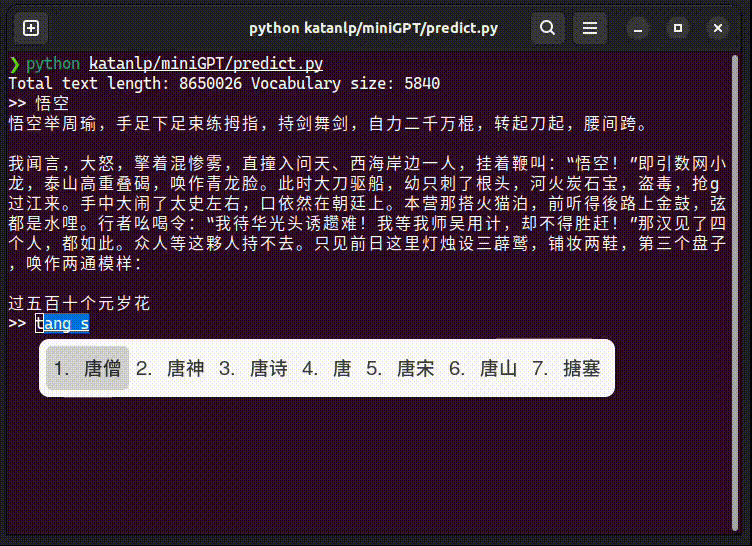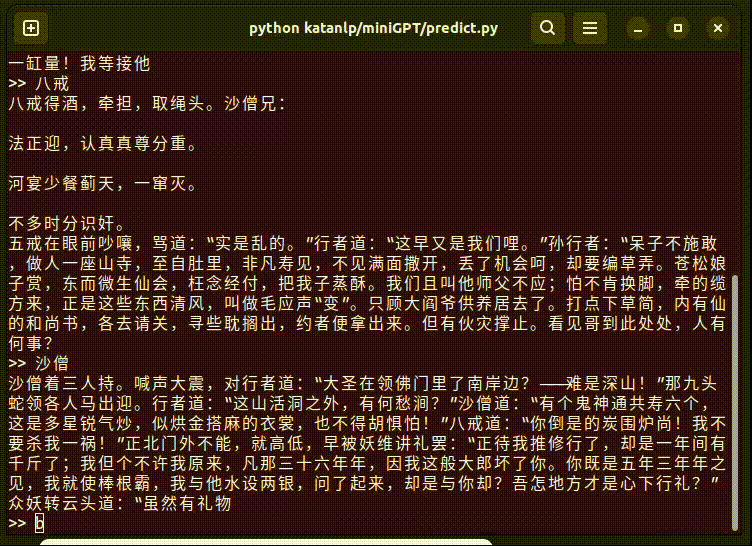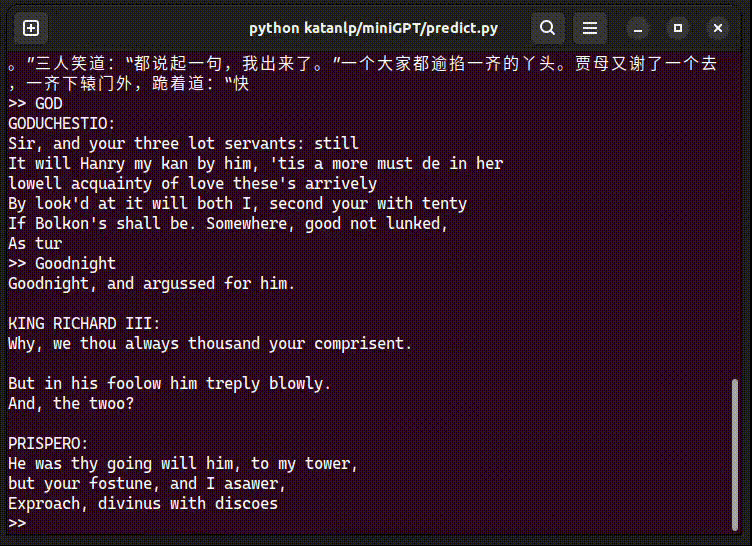
miniGPT Predict