2022 xjtu校赛 B题西安二手房房价分析 pandas数据分析 线性回归模型

题意

python整理代码

由于是第一次使用pandas进行数据分析，有很多不熟悉的地方，首先记录一下.

使用的是Jupyter Notebook完成，这个做数据分析确实非常好用，效果可以直接从网页中打开：

完整代码（颜色不清楚，请使用白色背景）：数据处理，回归分析-改进

使用的头文件，和绘图所用的参数

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.stats import kstest  # 进行k-s测试，判断是否满足正态分布，没用上
plt.rcParams['font.size'] = 20 # 固定字体大小
plt.rcParams['figure.figsize'] = (14, 6) # 固定图像大小
plt.rcParams['font.sans-serif']=['SimSun'] # 用来正常显示中文标签，使用宋体
plt.rcParams['axes.unicode_minus']=False # 用来正常显示负号

pandas中用到的重要函数：

以这个表格为例表格例子，data.xlsx：

	name	5_price	6_price	size	metro	bus	school	hospital	shop	city	year
0	恒大名都	NaN	13808	109.00	838.0	579.0	840.0	854.0	613.0	0	2012.0
1	锦园新世纪花园社区	NaN	15822	145.00	1007.0	845.0	220.0	221.0	210.0	0	2004.0
2	万科金色悦城	NaN	15352	72.00	833.0	719.0	467.0	1987.0	212.0	0	17.0
3	绿地香树花城	NaN	15345	72.00	1195.0	297.0	836.0	994.0	471.0	0	15.0
4	万科金域东郡	NaN	16539	281.00	611.0	561.0	984.0	654.0	842.0	0	17.0
...	...	...	...	...	...	...	...	...	...	...	...
355	世纪锦城	NaN	12373	122.08	238.0	150.0	513.0	123.0	501.0	11	13.0
356	怡景华庭	NaN	16630	101.00	103.0	176.0	436.0	712.0	371.0	11	7.0
357	奥林匹克花园二期	NaN	14491	127.00	761.0	238.0	658.0	300.0	324.0	11	16.0
358	同德晨曦园	NaN	12443	116.73	2500.0	129.0	279.0	290.0	263.0	11	16.0
359	紫薇万科大都会	NaN	15884	110.00	1900.0	280.0	1311.0	1086.0	802.0	11	19.0

360 rows × 11 columns

基础读入输出，简单分析

df = pd.read_excel('data.xlsx')  # 读取excel文件
df = pd.read_csv('data.csv')  # 读取csv文件
n, m = df.shape  # 读取全部行号与列号
n = df.shape[0]  # 读取行号
df.dtypes  # 查看每一列所列对应的数据类型，第一步检查数据，同一列的数据类型是否一致
df1 = df  # 这个是浅拷贝
df1 = df.copy()  # 这个是深拷贝
df['bus'].mean()  # 获取该列的均值
df['bus].std()  # 获取该列的标准差
df.describe()  # 显示表格的基本信息

df.describe() 可以获得以下信息

	5_price	6_price	size	metro	bus	school	hospital	shop	city	year
count	79.000000	318.000000	318.000000	318.000000	318.000000	318.000000	318.000000	318.000000	318.000000	318.000000
mean	15652.468354	15961.877358	119.421447	981.216981	515.022013	633.874214	957.610063	505.902516	5.679245	8.855346
std	3844.218722	4330.880408	31.193733	711.182323	284.119598	343.198506	798.500147	340.196742	3.411468	4.899413
min	8000.000000	7142.000000	38.000000	103.000000	44.000000	33.000000	61.000000	11.000000	0.000000	1.000000
25%	12781.000000	13451.750000	100.542500	544.250000	306.750000	367.250000	455.500000	244.500000	3.000000	5.000000
50%	14969.000000	15285.000000	117.070000	814.500000	464.000000	587.000000	768.500000	451.000000	6.000000	8.000000
75%	17853.000000	17626.250000	133.622500	1170.500000	673.750000	833.500000	1110.750000	695.000000	9.000000	12.000000
max	24597.000000	42113.000000	320.820000	5800.000000	2274.000000	2000.000000	5800.000000	1913.000000	11.000000	24.000000

获取与nan有关的信息

df['year'].isna()  # 判断 'year' 这一列是否为nan值
df[(df['year'].isna() | df['size'].isna())]  # 取出 'year' 或 'size' 为nan的行
df[-(df['year'].isna() | df['size'].isna())]  # 删去 'year' 或 'size' 为nan的行
df.reset_index(drop=True)  # 一般删去或重排行以后，行的index会变，需要重排，自动会在第一列 对于原有索引，加上drop=True可以删去这一列（一般都是多余的）

切片

切片均为深拷贝，下文中切片对应的是 pandas.core.series.Series 类，也就是切片类. 元素的类型与列的数据类型有关，不是 Series 类.

df['size']  # 取出 'size' 列的切片
df.loc[i]  # 取出索引为i行的切片
df.loc[0, 'size']  # 取出索引为0，'size' 列的元素
df.iloc[i]  # 取出相对坐标为i行的切片
df.iloc[i, j]  # 取出相对坐标为 (i, j) 的元素

对于比较复杂的表格，.loc[] 更加好用，因为可以根据列的名称来取元素，可读性更高. 但由于行索引不一定是连续的，所以一般重排表格后，会使用 reset_index() 把索引重排一遍.

绘图

主要使用函数 df.plot()，详细解释见 pandas.DataFrame.plot( )参数详解.

df['bus'].plot.hist()  # 最简单的柱状图
df['bus'].plot(kind='hist', bins=50, grid=True)  # 两种写法效果相同，推荐这种，更为一般化
# bins用于细分柱状条，grid用于显示网格

df['bus'].plot(kind='kde', label='概率密度分布')  # 绘制概率密度分布曲线

# 要想把两个图绘制在一起，考虑使用 ax.twinx() 的功能，增加一个y轴
ax1 = train['bus'].plot(kind = 'hist', bins=50, grid=True)  # 取出直方图的坐标轴ax1
plt.axis([0, 2400, 0, 23])  # 设定x,y轴范围
plt.xticks([x for x in range(2401) if x % 250 == 0])  # 设定步长
ax1.set_xlabel('公交站距离')  # 设定x,y轴标签
ax1.set_ylabel('个数')

ax2 = ax1.twinx()  # 创建第二y轴
train['bus'].plot(kind = 'kde', color='orange', label='概率密度分布', ax=ax2)  # 将坐标轴设为ax2
ax2.set_yticks([])  # 不显示概率分布的坐标值
ax2.set_ylabel('')  # 将'kde'生成的标签 Density 删去
plt.legend()  # 绘制标签

plt.savefig('bus.pdf')  # 保存图片
plt.show()  # 显示图片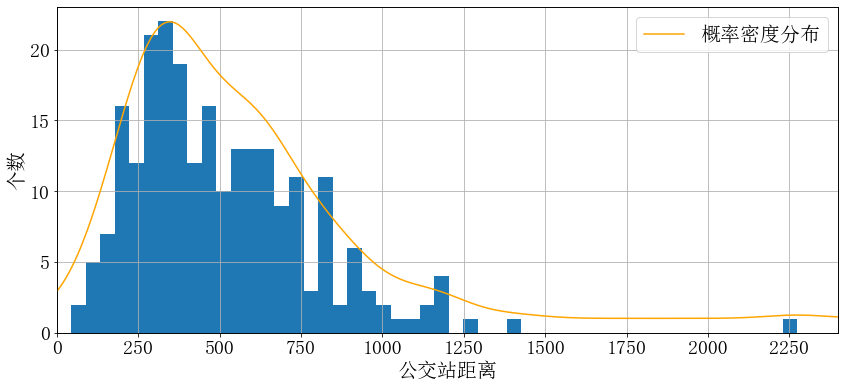

数据整理

这部分就很坑爹，需要自己在各大二手平台找各个小区的数据，如果会爬虫可能好一些，但是也肯定不容易. 我们人工找了 $360$ 个数据，通过上述方法将 $nan$ 值去除以后，筛选出了 $318$ 个有效数据，将训练集和验证集进行按照 $3:1$ 划分, 检验数据个数 $79$, 总计 $318$.

然后选择验证集中每个城区都均等分，一共12个城区，差不多在7到8个左右.

然后分析每一列的数据分布情况，从上图可以看出是基本满足正态分布的，也可以使用K-S检验，方法很简单：

from scipy.stats import kstest  # 引入kstest函数
kstest(df, 'norm', df.mean(), df.std())  # 只需给出数据列，均值和标准差即可
# 返回值为 statistic 和 pvalue，其中pvalue如果大于0.05则说明非常符合正态分布

效果其实不是很好，所以最终没有放到论文上去，但是大置曲线都是非常符合正态分布的. 绘图方法上文已经具体写了(绘图方法).

然后就是根据高斯分布，确定等级划分方法，思路是利用正态分布确定划分方法，设正态分布的均值为 $a$，标准差为 $\sigma$，高斯分布分为三个标准差范围即 $[a-\sigma,a+\sigma]$，$[a-2\sigma, a+2\sigma]$，$[a-3\sigma,a+3\sigma]$，所以我们分别根据正态分布分为五个等级，分别为

$$(-\infty, a-\sigma],\ [a-\sigma,a],\ [a, a+\sigma],\ [a+\sigma, a+2\sigma],\ [a+2\sigma,\infty)$$

如下图所示

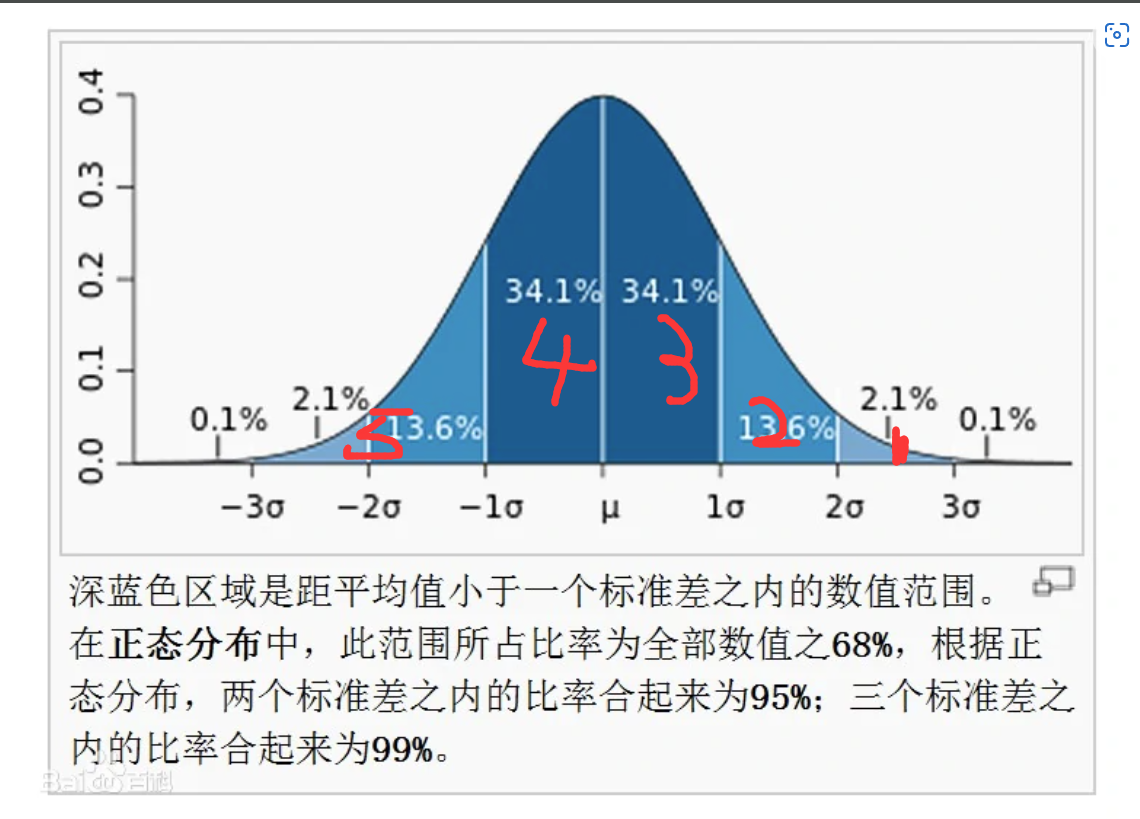
回归分析

原理如下，分为原版和改进以下后的版本（其实没什么很大的作用）

第一问

训练线性回归模型：单位平米房价与7种特征的关系

7种特征：地铁站距离，公交站距离，学校距离，医院距离，超市距离，所属市区，房龄. 设其对应的影响系数分别为 $a_i\ (i=1,2,\cdots, 7)$，线性回归模型为：

$$f(x_1,\cdots,x_7) = a_1x_1+\cdots +a_7 x_7+b = \sum_{i=1}^7 a_ix_i + b$$

其中 $b$ 为待定常数项，记自变量向量为 $\boldsymbol{x} = [x_1\quad x_2\quad\cdots\quad x_7\quad 1]^T$，系数向量为 $W = [a_1\quad a_2\quad \cdots\quad a_7\quad b]^T$. 则上式可写为如下形式

$$f(x_1,\cdots,x_7) = f(\boldsymbol{x}) = \boldsymbol{x}^TW$$

构造平方损失函数：

$$\mathcal{L}(\boldsymbol{x}, y) = \frac{1}{2}||y-\hat{y}||^2$$

其中 $y$ 为特征向量 $\boldsymbol{x}$ 所对应的标签，即单位平米房价，$\hat{y} = f(\boldsymbol{x})$ 为模型做出的预测值.

梯度下降法极小化最优化模型：

$$\min_{W\in \R^8} \mathcal{R}(W) =\sum_{(\boldsymbol{x}, y)\in \mathcal{D}}\mathcal{L}(\boldsymbol{x}, y)$$

其中 $\mathcal{D}$ 为训练集，包含 $239$ 个训练样本.

求解下降方向：

$$\boldsymbol{d} = \frac{\partial \mathcal{L}}{\partial W} = -\boldsymbol{x}(y-\boldsymbol{x}^TW)$$

则修改 $W$ 为：

$$W' = W - \alpha \overline{\boldsymbol{d}}$$

其中 $\alpha$ 为步长因子，这里取为 $1$，$\overline{\boldsymbol{d}} = \frac{\boldsymbol{d}}{||\boldsymbol{d}||}$ 即进行单位化.

结果：

$$W = \left[\begin{matrix} 335.57\\ 33.79\\ 239.66\\ 682.37\\ 335.81\\ 739.09\\ -221.18\\ 9052.36 \end{matrix}\right]\quad \text{sign}(W)\odot\log(\text{abs}(W)) = \left[\begin{matrix} 5.82\\ 3.52\\ 5.48\\ 6.53\\ 5.82\\ 6.61\\ -5.40\\ 9.11\\ \end{matrix}\right]\sim \left[\begin{matrix} \text{地铁站}\\ \text{公交站}\\ \text{学校}\\ \text{医院}\\ \text{超市}\\ \text{城区}\\ \text{房龄}\\ \text{常数项}\\ \end{matrix}\right]$$

其中 $\text{sign}(\cdot)$ 为取正负号，$\odot$ 为矩阵对应项相乘，$\text{abs}(\cdot)$ 为矩阵各项取绝对值.

评分计算式：

$$\text{score}(\boldsymbol{x})=5.82x_1 + 3.52x_2 + 5.48x_3 + 6.53x_4 + 5.82x_5 + 6.61x_6-5.40x_7$$

第二问：改进算法

原模型预测的结果准确率方差为 17.43，准确率在 -10%~10% 之间的数据有 35 个.

记训练集为 $\mathcal{T}$，验证集为 $\mathcal{E}$，改进风险函数如下：

$$\min_{W\in \R^8} \mathcal{R}(W) =\sum_{(\boldsymbol{x}, y)\in \mathcal{E}}\mathcal{L}(\boldsymbol{x}, y)$$

使用 $\mathcal{T}\cup\mathcal{E}$ 中的数据进行训j练模型，最终结果为

$$W = \left[\begin{matrix} 252.00\\ 321.86\\ 440.56\\ 610.56\\ 76.52\\ 419.73\\ -259.96\\ 10012.23 \end{matrix}\right]\quad \text{sign}(W)\odot\log(\text{abs}(W)) = \left[\begin{matrix} 5.53\\ 5.77\\ 6.09\\ 6.41\\ 4.34\\ 6.04\\ -5.56\\ 9.21\\ \end{matrix}\right]\sim \left[\begin{matrix} \text{地铁站}\\ \text{公交站}\\ \text{学校}\\ \text{医院}\\ \text{超市}\\ \text{城区}\\ \text{房龄}\\ \text{常数项}\\ \end{matrix}\right]$$

改进的模型预测的结果准确率方差为 15.92，准确率在 -10%~10% 之间的数据有 41 个，提高了 $6$ 个.

线性回归代码

关键：单位化下降方向（不然步长太大，无法收敛），初始值选取（选取标准正态分布，或者一个随机值）.

x = train.to_numpy()  # 先都转为np.array的形式
n = x.shape[0]  # 训练样本总数
W = np.array([np.random.rand()-0.5 for x in range(8)]) # W 初始化为 [-0.5, 0.5] 之间的随机值
W = W.reshape(-1, 1)  # 注意要转为二维向量
L = lambda: .5 * np.power(np.linalg.norm(y_train - x @ W), 2)  # 定义损失函数
print('初始loss: {}'.format(L()))
epoch = 10000  # 训练集使用次数
mn = 1e15  # 记录最小的loss值
best = W  # 存储最小loss值处的W向量
for T in range(epoch):  # 开始进行随机梯度下降
    for i in np.random.permutation(range(n)):  # 随机排列
        tx = x[i].reshape(1, -1)  # 特征
        ty = y_train[i].reshape(1, -1)  # 标签
        d = tx.T @ (ty - tx @ W) # 计算下降方向
        d /= np.linalg.norm(d) # 单位化
        W += d  # 更新
    if (L() < mn):  # 记录最小值
        mn = L()
        best = W.copy()
print(L())
print(mn)
print('best=\n{}\nW=\n{}'.format(best, W))
W = best

根据线性所得出的系数，得到每一种特征的重要性占比：

# 取log以后的系数（对非负部分取log）
metro: 5.82
bus: 3.52
school: 5.48
hospital: 6.53
shop: 5.82
city: 6.61
year: -5.40
const: 9.11

可以发现房龄是负贡献，这是符合现实情况的. 根据分布绘制饼状图如下：

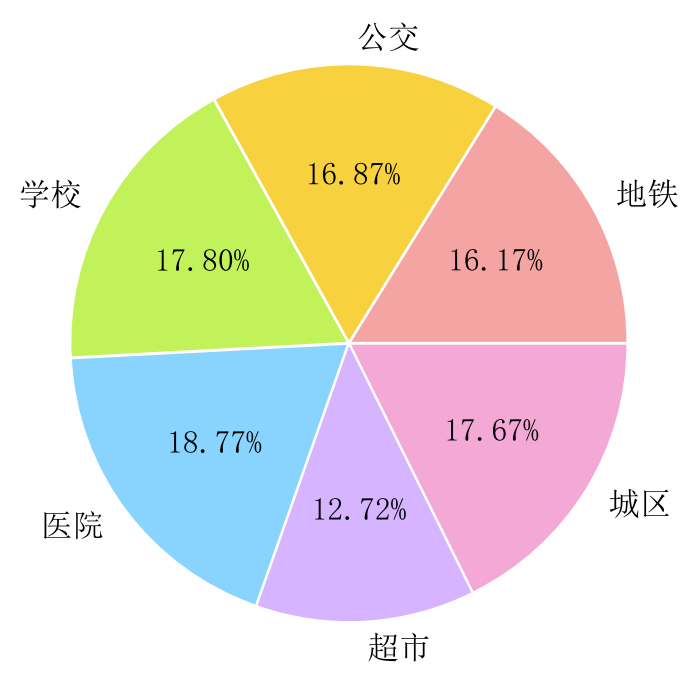
最后相同的方法绘制准确率分布即可.